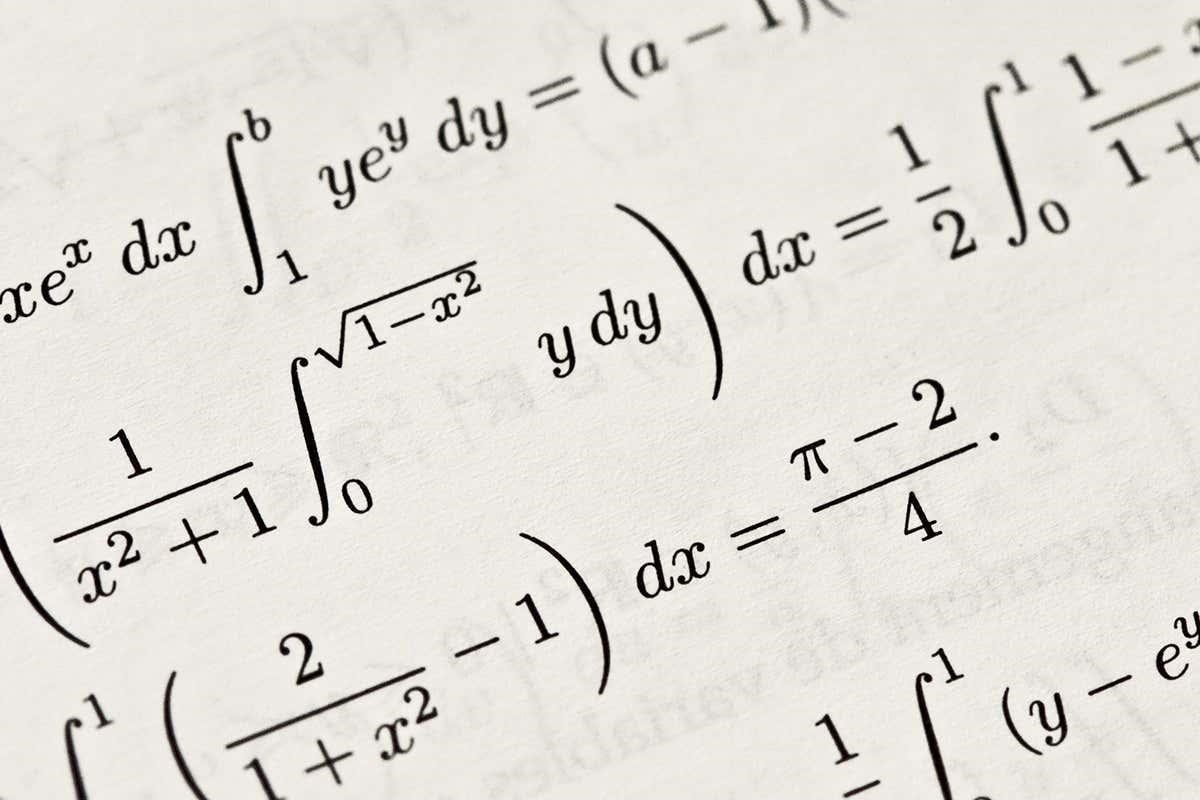Category: mathematics

Knot theory is linked to many other branches of science, including those that tell us about the cosmos.

The mathematical study of knots started with a mistake. In the 1800s, mathematician and physicist William Thomson, also known as Lord Kelvin, suggested that the elemental building blocks of matter were knotted vortices in the ether: invisible microscopic currents in the background material of the universe. His theory dropped by the wayside fairly quickly, but this first attempt to classify how curves could be knotted grew into the modern mathematical field of knot theory. Today, knot theory is not only connected to many branches of theoretical mathematics but also to other parts of science, like physics and molecular biology. It’s not obvious what your shoelace has to do with the shape of the universe, but the two may be more closely related than you think.

As it turns out, a tangled necklace offers a better model of a knot than a shoelace: to a mathematician, a knot is a loop in three-dimensional space rather than a string with loose ends. Just as a physical loop of string can stretch and twist and rotate, so can a mathematical knot – these loops are floppy rather than fixed. If we studied strings with free ends, they could wiggle around and untie themselves, but a loop stays knotted unless it’s cut.

Most questions in knot theory come in two varieties: sorting knots into classes and using knots to study other mathematical objects. I’ll try to give a flavour of both, starting with the simplest possible example: the unknot.

Draw a circle on a piece of paper. Congratulations, you’ve just constructed an unknot! This is the name for any loop in three-dimensional space that is the boundary of a disc. When you draw a circle on a piece of paper, you can see this disc as the space inside the circle, and your curve continues to be an unknot if you crumple the paper up, toss it through the air, flatten it out and then do some origami. As long as the disc is intact, no matter how distorted, the boundary is always an unknot.

Things get more interesting when you start with just the curve. How can you tell if it’s an unknot? There may secretly be a disc that can fill in the loop, but with no limits on how deformed the disc could be, it’s not clear how you can figure this out.

Two unknots

It turns out that this question is both hard and important: the first step in studying complicated objects is distinguishing them from simple ones. It’s also a question that gets answered inside certain bacterial cells each time they replicate. In the nuclei of these cells, the DNA forms a loop, rather than a strand with loose ends, and sometimes these loops end up knotted. However, the DNA can replicate only when the loop is an unknot, so the basic life processes of the cell require a process for turning a potentially complicated loop into an unknotted one.

A class of proteins called topoisomerases unknot tangled loops of DNA by cutting a strand, moving the free ends and then reattaching them. In a mathematical context, this operation is called a “crossing change”, and it’s known that any loop can be turned into the unknot by some number of crossing changes. However, there’s a puzzle in this process, since random crossing changes are unlikely to simplify a knot. Each topoisomerase operates locally, but collectively they’re able to reliably unknot the DNA for replication. Topoisomerases were discovered more than 50 years ago, but biologists are still studying how they unknot DNA so effectively.

When mathematicians want to identify a knot, they don’t turn to a protein to unknot it for them.  Instead, they rely on invariants, mathematical objects associated with knots. Some invariants are familiar things like numbers, while others are elaborate algebraic structures. The best invariants have two properties: they’re practical to compute, given the input of a specific knot, and they distinguish many different classes of knots from each other. It’s easy to define an invariant with only one of these properties, but a computable and effective knot invariant is a rare find.

The modern era of knot theory began with the introduction of an invariant called the Jones Polynomial in the 1980s. Vaughan Jones was studying statistical mechanics when he discovered a process that assigns a polynomial – a type of simple algebraic expression – to any knot. The method he used was technical, but the essential feature is that no amount of wiggling, stretching or twisting changes the output. The Jones Polynomial of an unknot is 1, no matter how complicated the associated disc might be.

Jones’s discovery caught the attention of other researchers, who found simpler techniques for computing the same polynomial. The result was an invariant that satisfies both the conditions listed above: the Jones Polynomial can be computed from a drawing of a knot on paper, and many thousands of knots can be distinguished by the fact that they have different Jones Polynomials.

However, there are still many things we don’t know about the Jones Polynomial, and one of the most tantalising questions is which knots it can detect. Most invariants distinguish some knots while lumping others together, and we say an invariant detects a knot if all the examples sharing a certain value are actually deformations of each other. There are certainly pairs of distinct knots with the same Jones Polynomial, but after decades of study, we still don’t know whether any knot besides the unknot has the polynomial 1. With computer assistance, experts have examined nearly 60 trillion examples of distinct knots without finding any new knots whose Jones Polynomials equal 1.

The Jones Polynomial has applications beyond knot detection. To see this, let’s return to the definition of an unknot as a loop that bounds a disc. In fact, every knot is the boundary of some surface – what distinguishes an unknot is that this surface is particularly simple. There’s a precise way to rank the complexity of surfaces, and we can use this to rank the complexity of knots. In this classification, the simplest knot is the unknot, and the second simplest is the trefoil, which is shown below.

Trefoil knot

To build a surface with a trefoil boundary, start with a strip of paper. Twist it three times and then glue the ends together. This is more complicated than a disc, but still pretty simple. It also gives us a new question to investigate: given an arbitrary knot, where does it fit in the ranking of knot complexity? What’s the simplest surface it can bound? Starting with a curve and then hunting for a surface may seem backwards, but in some settings, the Jones Polynomial answers this question: the coefficients of the knot polynomial can be used to estimate the complexity of the surfaces it bounds.

Joan Licata

Knots also help us classify other mathematical objects. We can visually distinguish the two-dimensional surface of sphere from the surface a torus (the shape of a ring donut), but an ant walking on one of these surfaces might need knot theory to tell them apart. On the surface of a torus, there are loops that can’t be pulled any tighter, while any loop lying on a sphere can contract to a point.

We live inside a universe of three physical dimensions, so like the ant on a surface, we lack a bird’s eye view that could help us identify its global shape. However, we can ask the analogous question: can each loop we encounter shrink without breaking, or is there a shortest representative? Mathematicians can classify three-dimensional spaces by the existence of the shortest knots they contain. Presently, we don’t know if some knots twisting through the universe are unfathomably long or if every knot can be made as small as one of Lord Kelvin’s knotted vortices.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Joan Licata*

Artificial intelligence firm DeepMind has tackled games like Go and Starcraft, but now it is turning its attention to more sober affairs: how to solve school-level maths problems.

Researchers at the company tasked an AI with teaching itself to solve arithmetic, algebra and probability problems, among others. It didn’t do a very good job: when the neural network was tested on a maths exam taken by 16-year-olds in the UK, it got just 14 out of 40 questions correct, or the equivalent of an E grade.

There were also strange quirks in the AI’s ability. For example, it could successfully add up 1+1+1+1+1+1 to make 6, but failed when an extra 1 was added. On the other hand, it gave the correct answer for longer sequences and much bigger numbers.

Other oddities included the ability to correctly answer 68 to the question “calculate 17×4.”, but when the full stop was removed, the answer came out at 69.

Puzzling behaviour

The DeepMind researchers concede they don’t have a good explanation for this behaviour. “At the moment, learning systems like neural networks are quite bad at doing ‘algebraic reasoning’,” says David Saxton, one of the team behind the work.

Despite this, it is still worth trying to teach a machine to solve maths problems, says Marcus du Sautoy, a mathematician at the University of Oxford.

“There are already algorithms out there to do these problems much faster, much better than machine-learning algorithms, but that’s not the point,” says du Sautoy. “They are setting themselves a different target – we want to start from nothing, by being told whether you got that one wrong, that one right, whether it can build up how to do this itself. Which is fascinating.”

An AI capable of solving advanced mathematics problems could put him out of a job, says du Sautoy. “That’s my fear. It may not take too much for an AI to get maturity in this world, whereas a maturity in the musical or visual or language world might be much harder for it. So I do think my subject is vulnerable.”

However, he takes some comfort that machine learning’s general weakness in remaining coherent over a long form – such as a novel, rather than a poem – will keep mathematicians safe for now. Creating mathematical proofs, rather than solving maths problems for 16-year-olds, will be difficult for machines, he says.

Noel Sharkey at the University of Sheffield, UK, says the research is more about finding the limits of machine-learning techniques, rather than promoting advancements in mathematics.

The interesting thing, he says, will be to see how the neural networks can adapt to challenges outside of those they were trained on. “The big question is to ask how well they can generalise to novel examples that were not in the training set. This has the potential to demonstrate formal limits to what this type of learning is capable of.”

Saxton says training a neural network on maths problems could help provide AI with reasoning skills for other applications.

“Humans are good at maths, but they are using general reasoning skills that current artificial learning systems don’t possess,” he says. “If we can develop models that are good at solving these problems, then these models would likely be using general skills that would be good at solving other hard problems in AI as well.”

He hopes the work could make a small contribution towards more general mathematical AIs that could tackle things such as proving theorems.

The DeepMind team has published its data set of maths questions, and encouraged people to train their own AI.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Adam Vaughan*

It’s a bit more complicated than this

Forget your times tables – mathematicians have found a new, faster way to multiply two numbers together. The method, which works only for whole numbers, is a landmark result in computer science. “This is big news,” says Joshua Cooper at the University of South Carolina.

To understand the new technique, which was devised by David Harvey at the University of New South Wales, Australia, and Joris van der Hoeven at the Ecole Polytechnique near Paris, France, it helps to think back to the longhand multiplication you learned at school.

We write down two numbers, one on top of the other, and then painstakingly multiply each digit of one by each digit of the other, before adding all the results together. “This is an ancient algorithm,” says Cooper.

If your two numbers each have n digits, this way of multiplying will require roughly n² individual calculations. “The question is, can you do better?” says Cooper.

Lots of logs

Starting in the 1960s, mathematicians began to prove that they could. First Anatoly Karatsuba found an algorithm that could turn out an answer in no more than n^1.58 steps, and in 1971, Arnold Schönhage and Volker Strassen found a way to peg the number of steps to the complicated expression n*(log(n))*log(log(n)) – here “log” is short for logarithm.

These advances had a major impact on computing. Whereas a computer using the longhand multiplication method would take about six months to multiply two billion-digit numbers together, says Harvey, the Schönhage-Strassen algorithm can do it in 26 seconds.

The landmark 1971 paper also suggested a possible improvement, a tantalising prediction that multiplication might one day be possible in no more than n*log(n) steps. Now Harvey and van der Hoeven appear to have proved this is the case. “It finally appears to be possible,” says Cooper. “It passes the smell test.”

“If the result is correct, it’s a major achievement in computational complexity theory,” says Fredrik Johansson at INRIA, the French research institute for digital sciences, in Bordeaux. “The new ideas in this work are likely to inspire further research and could lead to practical improvements down the road.”

Cooper also praises the originality of the research, although stresses the complexity of the mathematics involved. “You think, jeez, I’m just multiplying two integers, how complicated can it get?” says Cooper. “But boy, it gets complicated.”

So, will this make calculating your tax returns any easier? “For human beings working with pencil and paper, absolutely not,” says Harvey. Indeed, their version of the proof only works for numbers with more than 10 to the power of 200 trillion trillion trillion digits. “The word ‘astronomical’ falls comically short in trying to describe this number,” says Harvey.

While future improvements to the algorithm may extend the proof to more humdrum numbers only a few trillion digits long, Cooper thinks its real value lies elsewhere. From a theoretical perspective, he says, this work allows programmers to provide a definitive guarantee of how long a certain algorithm will take. “We are optimistic that our new paper will allow us to achieve further practical speed-ups,” says van der Hoeven.

Harvey thinks this may well be the end of the story, with no future algorithm capable of beating n*log(n). “I would be extremely surprised if this turned out to be wrong,” he says, “but stranger things have happened.”

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Gilead Amit*

The number 33 has surprising depth

Add three cubed numbers, and what do you get? It is a question that has puzzled mathematicians for centuries.

In 1825, a mathematician known as S. Ryley proved that any fraction could be represented as the sum of three cubes of fractions. In the 1950s, mathematician Louis Mordell asked whether the same could be done for integers, or whole numbers. In other words, are there integers k, x, y and z such that k = x³ + y³ + z³ for each possible value of k?

We still don’t know. “It’s long been clear that there are maths problems that are easy to state, but fiendishly hard to solve,” says Andrew Booker at the University of Bristol, UK – Fermat’s last theorem is a famous example.

Booker has now made another dent in the cube problem by finding a sum for the number 33, previously the lowest unsolved example. He used a computer algorithm to search for a solution:

33 = 8,866,128,975,287,528³ + (-8,778,405,442,862,239)³ + (-2,736,111,468,807,040)³

To cut down calculation time, the program eliminated certain combinations of numbers. “For instance, if x, y and z are all positive and large, then there’s no way that x³ + y³ + z³ is going to be a small number,” says Booker. Even so, it took 15 years of computer-processing time and three weeks of real time to come up with the result.

For some numbers, finding a solution to the equation k = x³ + y³ + z³ is simple, but others involve huge strings of digits. “It’s really easy to find solutions for 29, and we know a solution for 30, but that wasn’t found until 1999, and the numbers were in the millions,” says Booker.

Another example is for the number 3, which has two simple solutions: 1³ + 1³ + 1³  and 4³ + 4³ + (-5) ³ . “But to this day, we still don’t know whether there are more,” he says.

There are certain numbers that we know definitely can’t be the sum of three cubes, including 4, 5, 13, 14 and infinitely many more.

The solution to 74 was only found in 2016, which leaves 42 as the only number less than 100 without a possible solution. There are still 12 unsolved numbers less than 1000.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Donna Lu*

Today I’d like to share an idea. It’s a very simple idea. It’s not fancy and it’s certainly not new. In fact, I’m sure many of you have thought about it already. But if you haven’t—and even if you have!—I hope you’ll take a few minutes to enjoy it with me. Here’s the idea:

So simple! But we can get a lot of mileage out of it.

To start, I’ll be a little more precise: every matrix corresponds to a weighted bipartite graph. By “graph” I mean a collection of vertices (dots) and edges; by “bipartite” I mean that the dots come in two different types/colors; by “weighted” I mean each edge is labeled with a number.

The graph above corresponds to a 3×23×2 matrix MM. You’ll notice I’ve drawn three greengreen dots—one for each row of MM—and two pinkpink dots—one for each column of MM. I’ve also drawn an edge between a green dot and a pink dot if the corresponding entry in MM is non-zero.

For example, there’s an edge between the second green dot and the first pink dot because M21=4M21=4, the entry in the second row, first column of MM, is not zero. Moreover, I’ve labeled that edge by that non-zero number. On the other hand, there is no edge between the first green dot and the second pink dot because M12M12, the entry in the first row, second column of the matrix, is zero.

Allow me to describe the general set-up a little more explicitly.

Any matrix MM is an array of n×mn×m numbers. That’s old news, of course. But such an array can also be viewed as a function M:X×Y→RM:X×Y→R where X={x1,…,xn}X={x1,…,xn} is a set of nn elements and Y={y1,…,ym}Y={y1,…,ym} is a set of mm elements. Indeed, if I want to describe the matrix MM to you, then I need to tell you what each of its ijijth entries are. In other words, for each pair of indices (i,j)(i,j), I need to give you a real number MijMij. But that’s precisely what a function does! A function M:X×Y→RM:X×Y→R associates for every pair (xi,yj)(xi,yj) (if you like, just drop the letters and think of this as (i,j)(i,j)) a real number M(xi,yj)M(xi,yj). So simply write MijMij for M(xi,yj)M(xi,yj).

Et voila. A matrix is a function.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*

I am often asked the question, “How do you do it?!” Now while I don’t think my note-taking strategy is particularly special, I am happy to share! I’ll preface the information by stating what you probably already know: I LOVE to write.* I am a very visual learner and often need to go through the physical act of writing things down in order for information to “stick.” So while some people think aloud (or quietly),

I think on paper.

My study habits, then, are built on this fact. Of course not everyone learns in this way, so this post is not intended to be a how-to guide. It’s just a here’s-what-I-do guide.

With that said, below is a step-by-step process I tried to follow during my final years of undergrad and first two years of grad school.**

‍Step 1

Read the appropriate chapter/section in the book before class

I am an “active reader,” so my books have tons of scribbles, underlines, questions, and “aha” moments written on the pages. I like to write while I read because it gives me time to pause and think about the material. For me, reading a mathematical text is not like reading a novel. It often takes me a long time just to understand a single paragraph! Or a single sentence. I also like to mark things that I don’t understand so I’ll know what to look for in the upcoming lecture.

STEP 2

Attend lecture and take notes

This step is pretty self-explanatory, but I will mention this: I write down much more than what is written on the chalkboard (or whiteboard). In fact, a good portion of my in-class notes consists of what the professor has said but hasn’t written.

‍My arsenal

‍STEP 3

Rewrite lecture notes at home

My in-class notes are often an incomprehensible mess of frantically-scribbled hieroglyphs. So when I go home, I like to rewrite everything in a more organized fashion. This gives the information time to simmer and marinate in my brain. I’m able to ponder each statement at my own pace, fill in any gaps, and/or work through any exercises the professor might have suggested. I’ll also refer back to the textbook as needed.

Sometimes while rewriting these notes, I’ll copy things word-for-word (either from the lecture, the textbook, or both), especially if the material is very new or very dense. Although this can be redundant, it helps me slow down and lets me think about what the ideas really mean. Other times I’ll just rewrite things in my own words in a way that makes sense to me.

A semester’s worth of notes!

As for the content itself, my notes usually follow a “definition then theorem then proof” outline, simply because that’s how material is often presented in the lecture. But sometimes it’s hard to see the forest for the trees (i.e. it’s easy to get lost in the details), so I’ll occasionally write “PAUSE!” or “KEY IDEA!” in the middle of the page. I’ll then take the time to write a mini exposition that summarizes the main idea of the previous pages. I’ve found this to be especially helpful when looking back at my notes after several months (or years) have gone by. I may not have time to read all the details/calculations, so it’s nice to glance at a summary for a quick refresher.

And every now and then, I’ll rewrite my rewritten notes in the form of a SaiBlog post! Many of my earlier posts here at Math3ma were “aha” moments that are now engrained in my brain because I took the time to SaiBlog about them.

STEP 4

Do homework problems

Once upon a time, I used to think the following:

How can I do problems if I haven’t spent a bajillion hours learning the theory first?

But now I believe there’s something to be said for the converse: 

How can I understand the theory if I haven’t done a bajillion examples first?

In other words, taking good notes and understanding theory is one thing, but putting that theory into practice is a completely different beast. As a wise person once said, “The only way to learn math is to DO math.” So although I’ve listed “do homework problems” as the last step, I think it’s really first in terms of priority.

Typically, then, I’ll make a short to-do list (which includes homework assignments along with other study-related duties) each morning. And I’ll give myself a time limit for each task. For example, something like “geometry HW, 3 hours” might appear on my list, whereas “do geometry today” will not. Setting a time gives me a goal to reach for which helps me stay focused. And I may be tricking my brain here, but a specific, three-hour assignment sounds much less daunting than an unspecified, all-day task. (Of course, my lists always contain multiple items that take several hours each, but as the old adage goes, “How do you eat an elephant? One bite at a time.”)

By the way, in my first two years of grad school I often worked with my classmates on homework problems. I didn’t do this in college, but in grad school I’ve found it tricky to digest all the material alone – there’s just too much of it! So typically I’d first attempt exercises on my own, then meet up with a classmate or two to discuss our ideas and solutions and perhaps attend office hours with any questions.

As far as storage goes, I have a huge binder that contains all of my rewritten notes*** from my first and second year classes. (I use sheet protectors to keep them organized according to subject.) On the other hard, I use a paper tray like this one to store my lecture notes while the semester is in progress. Once classes are over, I’ll scan and save them to an external hard drive. I’ve also scanned and saved all my homework assignments.

Well, I think that’s about it! As I mentioned earlier, these steps were only my ideal plan. I often couldn’t apply them to every class — there’s just not enough time! — so I’d only do it for my more difficult courses. And even then, there might not be enough time for steps 1 and 3, and I’d have to start working on homework right after a lecture.

But as my advisor recently told me,”It’s okay to not know everything.” Indeed, I think the main thing is to just do something. Anything. As much as you can. And as time goes on, you realize you really are learning something, even if it doesn’t feel like it at the time.

Alright, friends, I think that’s all I have to share. I hope it was somewhat informative. If you have any questions, don’t hesitate to leave it in a comment below!

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*

Mathematicians are stunned by the discovery that prime numbers are pickier than previously thought. The find suggests number theorists need to be a little more careful when exploring the vast infinity of primes.

Primes, the numbers divisible only by themselves and 1, are the building blocks from which the rest of the number line is constructed, as all other numbers are created by multiplying primes together. That makes deciphering their mysteries key to understanding the fundamentals of arithmetic.

Although whether a number is prime or not is pre-determined, mathematicians don’t have a way to predict which numbers are prime, and so tend to treat them as if they occur randomly. Now Kannan Soundararajan and Robert Lemke Oliver of Stanford University in California have discovered that isn’t quite right.

“It was very weird,” says Soundararajan. “It’s like some painting you are very familiar with, and then suddenly you realise there is a figure in the painting you’ve never seen before.”

Surprising order

So just what has got mathematicians spooked? Apart from 2 and 5, all prime numbers end in 1, 3, 7 or 9 – they have to, else they would be divisible by 2 or 5 – and each of the four endings is equally likely. But while searching through the primes, the pair noticed that primes ending in 1 were less likely to be followed by another prime ending in 1. That shouldn’t happen if the primes were truly random – consecutive primes shouldn’t care about their neighbour’s digits.

“In ignorance, we thought things would be roughly equal,” says Andrew Granville of the University of Montreal, Canada. “One certainly believed that in a question like this we had a very strong understanding of what was going on.”

The pair found that in the first hundred million primes, a prime ending in 1 is followed by another ending in 1 just 18.5 per cent of the time. If the primes were distributed randomly, you’d expect to see two 1s next to each other 25 per cent of the time. Primes ending in 3 and 7 take up the slack, each following a 1 in 30 per cent of primes, while a 9 follows a 1 in around 22 per cent of occurrences.

Similar patterns showed up for the other combinations of endings, all deviating from the expected random values. The pair also found them in other bases, where numbers are counted in units other than 10s. That means the patterns aren’t a result of our base-10 numbering system, but something inherent to the primes themselves. The patterns become more in line with randomness as you count higher – the pair have checked up to a few trillion – but still persists.

“I was very surprised,” says James Maynard of the University of Oxford, UK, who on hearing of the work immediately performed his own calculations to check the pattern was there. “I somehow needed to see it for myself to really believe it.”

Stretching to infinity

Thankfully, Soundararajan and Lemke Oliver think they have an explanation. Much of the modern research into primes is underpinned G H Hardy and John Littlewood, two mathematicians who worked together at the University of Cambridge in the early 20^th century. They came up with a way to estimate how often pairs, triples and larger grouping of primes will appear, known as the k-tuple conjecture.

Just as Einstein’s theory of relativity is an advance on Newton’s theory of gravity, the Hardy-Littlewood conjecture is essentially a more complicated version of the assumption that primes are random – and this latest find demonstrates how the two assumptions differ. “Mathematicians go around assuming primes are random, and 99 per cent of the time this is correct, but you need to remember the 1 per cent of the time it isn’t,” says Maynard.

The pair used Hardy and Littlewood’s work to show that the groupings given by the conjecture are responsible for introducing this last-digit pattern, as they place restrictions on where the last digit of each prime can fall. What’s more, as the primes stretch to infinity, they do eventually shake off the pattern and give the random distribution mathematicians are used to expecting.

“Our initial thought was if there was an explanation to be found, we have to find it using the k-tuple conjecture,” says Soundararajan. “We felt that we would be able to understand it, but it was a real puzzle to figure out.”

The k-tuple conjecture is yet to be proven, but mathematicians strongly suspect it is correct because it is so useful in predicting the behaviour of the primes. “It is the most accurate conjecture we have, it passes every single test with flying colours,” says Maynard. “If anything I view this result as even more confirmation of the k-tuple conjecture.”

Although the new result won’t have any immediate applications to long-standing problems about primes like the twin-prime conjecture or the Riemann hypothesis, it has given the field a bit of a shake-up. “It gives us more of an understanding, every little bit helps,” says Granville. “If what you take for granted is wrong, that makes you rethink some other things you know.”

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Jacob Aron*

Yesterday I received a disheartening 44/50 on a homework assignment. Okay okay, I know. 88% isn’t bad, but I had turned in my solutions with so much confidence that admittedly, my heart dropped a little (okay, a lot!) when I received the grade. But I quickly had to remind myself, Hey! Grades don’t matter.

The six points were deducted from two problems. (Okay, fine. It was three. But in the third I simply made an air-brained mistake.) In the first, apparently my answer wasn’t explicit enough. How stingy! I thought. Doesn’t our professor know that this is a standard example from the book? I could solve it in my sleep! But after the prof went over his solution in class, I realized that in all my smugness I never actually understood the nuances of the problem. Oops. You bet I’ll be reviewing his solution again. Lesson learned.

In the second, I had written down my solution in the days before and had checked with a classmate and (yes) the internet to see if I was correct. Unfortunately, the odds were against me two-to-one as both sources agreed with each other but not with me. But I just couldn’t see how I could possibly be wrong! Confident that my errors were truths, I submitted my solution anyway, hoping there would be no consequences. But alas, points were taken off.

Honestly though, is a lower grade such a bad thing? I think not. In both cases, I learned exactly where my understanding of the material went awry. And that’s great! It means that my comprehension of the math is clearer now than it was before (and that the chances of passing my third qualifying exam have just increased. Woo!) And that’s precisely why I’m (still, heh…) in school.

So yes, contrary to what the comic above says, grades do exist in grad school, but – and this is what I think the comic is hinting at – they don’t matter. Your thesis committee members aren’t going to say, “Look, your defense was great, but we can’t grant you your PhD. Remember that one homework/midterm/final grade from three years ago?” (They may not use the word “great” either, but that’s another matter.) Of course, we students should still work hard and put in maximum effort! But the emphasis should not be on how well we perform, but rather how much we learn. Focus on the latter and the former will take care of itself. This is true in both graduate school and college, but the lack of emphasis on grades in grad school really brings it home. And personally, I’m very grateful for it because my brain is freed up to focus on other things like, I don’t know, learning math!

So to all my future imperfect homework scores out there: bring it on.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*

A maths problem previously tackled with the help of a computer, which produced a proof the size of Wikipedia, has now been cut down to size by a human. Although it is unlikely to have practical applications, the result highlights the differences between two modern approaches to mathematics: crowdsourcing and computers.

Terence Tao of the University of California, Los Angeles, has published a proof of the Erdős discrepancy problem, a puzzle about the properties of an infinite, random sequence of +1s and -1s. In the 1930s, Hungarian mathematician Paul Erdős wondered whether such a sequence would always contain patterns and structure within the randomness.

One way to measure this is by calculating a value known as the discrepancy. This involves adding up all the +1s and -1s within every possible sub-sequence. You might think the pluses and minuses would cancel out to make zero, but Erdős said that as your sub-sequences got longer, this sum would have to go up, revealing an unavoidable structure. In fact, he said the discrepancy would be infinite, meaning you would have to add forever, so mathematicians started by looking at smaller cases in the hopes of finding clues to attack the problem in a different way.

Last year, Alexei Lisitsa and Boris Konev of the University of Liverpool, UK used a computer to prove that the discrepancy will always be larger than two. The resulting proof was a 13 gigabyte file – around the size of the entire text of Wikipedia – that no human could ever hope to check.

Helping hands

Tao has used more traditional mathematics to prove that Erdős was right, and the discrepancy is infinite no matter the sequence you choose. He did it by combining recent results in number theory with some earlier, crowdsourced work.

In 2010, a group of mathematicians, including Tao, decided to work on the problem as the fifth Polymath project, an initiative that allows professionals and amateurs alike to contribute ideas through SaiBlogs and wikis as part of mathematical super-brain. They made some progress, but ultimately had to give up.

“We had figured out an interesting reduction of the Erdős discrepancy problem to a seemingly simpler problem involving a special type of sequence called a completely multiplicative function,” says Tao.

Then, in January this year, a new development in the study of these functions made Tao look again at the Erdős discrepancy problem, after a commenter on his SaiBlog pointed out a possible link to the Polymath project and another problem called the Elliot conjecture.

Not just conjecture

“At first I thought the similarity was only superficial, but after thinking about it more carefully, and revisiting some of the previous partial results from Polymath5, I realised there was a link: if one could prove the Elliott conjecture completely, then one could also resolve the Erdős discrepancy problem,” says Tao.

“I have always felt that that project, despite not solving the problem, was a distinct success,” writes University of Cambridge mathematician Tim Gowers, who started the Polymath project and hopes that others will be encouraged to participate in future. “We now know that Polymath5 has accelerated the solution of a famous open problem.”

Lisitsa praises Tao for doing what his algorithm couldn’t. “It is a typical example of high-class human mathematics,” he says. But mathematicians are increasingly turning to machines for help, a trend that seems likely to continue. “Computers are not needed for this problem to be solved, but I believe they may be useful in other problems,” Lisitsa says.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Jacob Aron*

Felker prefaces the quote by saying,

Giving up on math means you don’t believe that careful study can change the way you think.

He further notes that writing, like math, “is also not something that anyone is ‘good’ at without a lot of practice, but it would be completely unacceptable to think that your composition skills could not improve.”

Friends, this is so true! Being ‘good’ at math boils down to hard work and perseverance, not whether or not you have the ‘math gene.’ “But,” you might protest, “I’m so much slower than my classmates are!” or “My educational background isn’t as solid as other students’!” or “I got a late start in mathematics!”* That’s okay! A strong work ethic and a love and enthusiasm for learning math can shore up all deficiencies you might think you have. Now don’t get me wrong. I’m not claiming it’ll be a walk in the park. To be honest, some days it feels like a walk through an unfamiliar alley at nighttime during a thunderstorm with no umbrella. But, you see, that’s okay too. It may take some time and the road may be occasionally bumpy, but it can be done!

This brings me to another point that Felker makes: If you enjoy math but find it to be a struggle, do not be discouraged! The field of math is HUGE and its subfields come in many different flavors. So for instance, if you want to be a math major but find your calculus classes to be a challenge, do not give up! This is not an indication that you’ll do poorly in more advanced math courses. In fact, upper level math classes have a completely (I repeat, completely!) different flavor than calculus. Likewise, in graduate school you may struggle with one course, say algebraic topology, but find another, such as logic, to be a breeze. Case in point: I loathed real analysis as an undergraduate** and always thought it was pretty masochistic. But real analysis in graduate school was nothing like undergraduate real analysis (which was more like advanced calculus), and now – dare I say it? – I sort of enjoy the subject. (Gasp!)

All this to say that although Felker’s article is aimed at folks who may be afraid to take college-level math, I think it applies to math majors and graduate students too. I highly recommend you read it if you ever need a good ‘pick-me-up.’ And on those days when you feel like the math struggle is harder than usual, just remember:

Even the most accomplished mathematicians had to learn HOW to learn this stuff!

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*