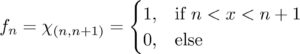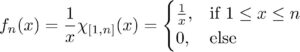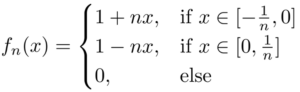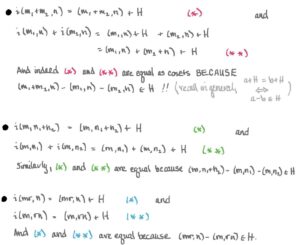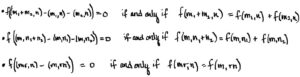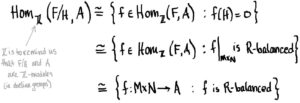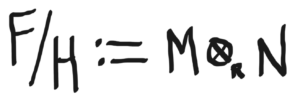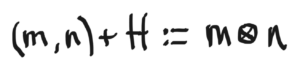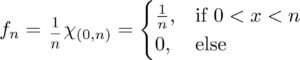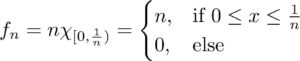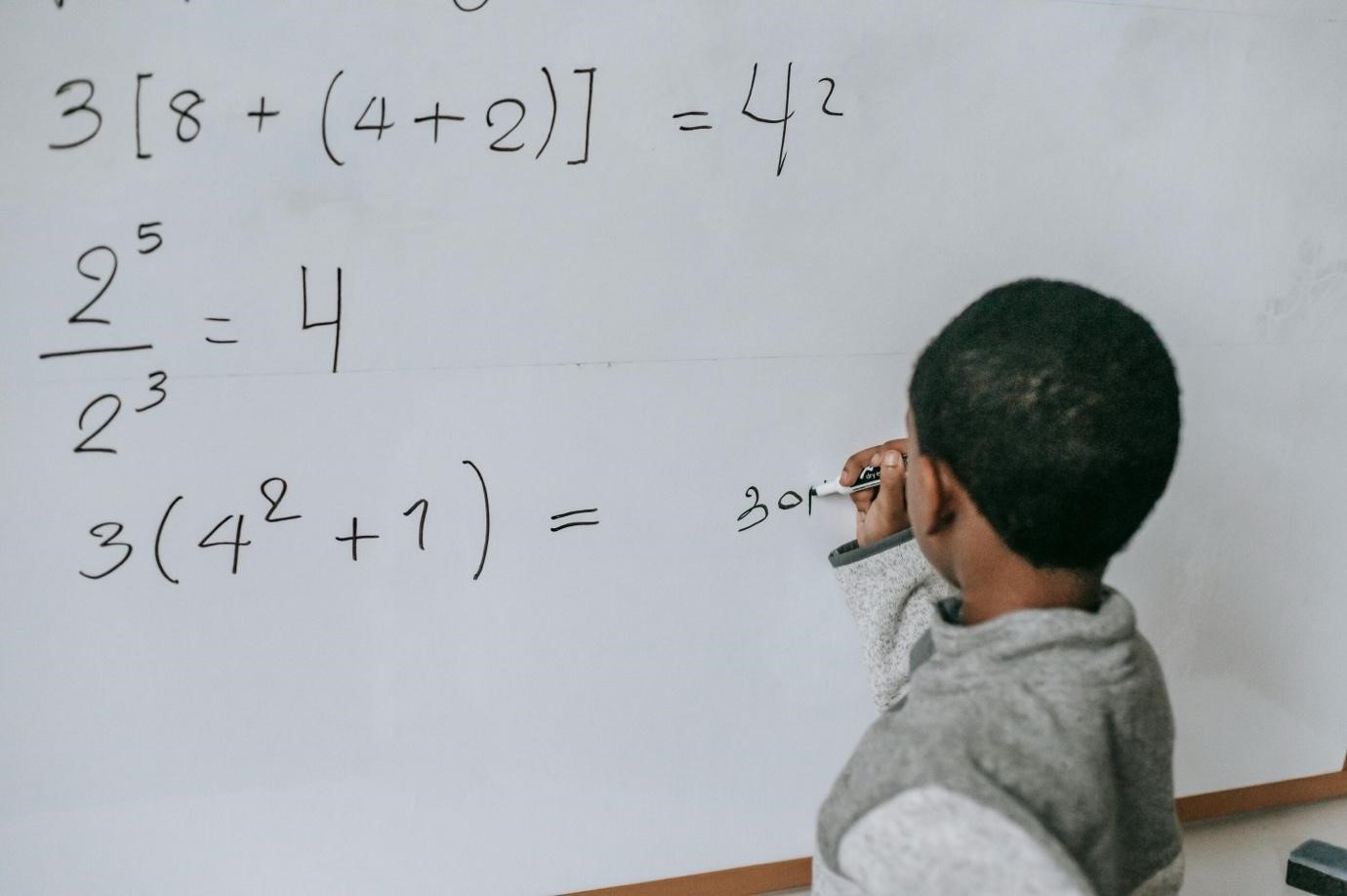Category: mathematics

Example 5

A sequence of functions {fn:R→R}{fn:R→R} which converges to 0 pointwise but does not converge to 0 in L1L1.

This works because: The sequence tends to 0 pointwise since for a fixed x∈Rx∈R, you can always find N∈NN∈N so that fn(x)=0fn(x)=0 for all nn bigger than NN. (Just choose N>xN>x!)

The details: Let x∈Rx∈R and fix ϵ>0ϵ>0 and choose N∈NN∈N so that N>xN>x. Then whenever n>Nn>N, we have |fn(x)−0|=0<ϵ|fn(x)−0|=0<ϵ.

Of course, fn↛0fn↛0 in L1L1 since∫R|fn|=∫(n,n+1)fn=1⋅λ((n,n+1))=1.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*

Suffixes are important!

Did you know that the words

“maximal” and “maximum” generally do NOT mean the same thing

in mathematics? It wasn’t until I had to think about Zorn’s Lemma in the context of maximal ideals that I actually thought about this, but more on that in a moment. Let’s start by comparing the definitions:

Do you see the difference? An element is a maximum if it is larger than every single element in the set, whereas an element is maximal if it is not smaller than any other element in the set (where “smaller” is determined by the partial order ≤≤). Yes, it’s true that the* maximum also satisfies this property, i.e. every maximum element is also maximal. But the converse is not true: if an element is maximal, it may not be the maximum! Why? The key is that these definitions are made on a partially ordered set. Basically, partially ordered just means it makes sense to use the words “bigger” or “smaller” – we have a way to compare elements. In a totally ordered set ALL elements are comparable with each other. But in a partially ordered set SOME, but not necessarily all, elements can be compared. This means it’s possible to have an element that is maximal yet fails to be the maximum because it cannot be compared with some elements. It’s not too hard to see that when a set is totally ordered, “maximal = maximum.”**

How about an example? Here’s one I like from this scholarly site which also gives an example of a miminal/minimum element (whose definitions are dual to those above).

Example

Consider the set

where the partial order is set inclusion, ⊆⊆. Then

• {d,o}{d,o} is minimalbecause {d,o}⊉x{d,o}⊉x for every x∈Xx∈
• e. there isn’t a single element in XX that is “smaller” than {d,o}{d,o}
• {g,o,a,d}{g,o,a,d} is maximalbecause {g,o,a,d}⊈x{g,o,a,d}⊈x for every x∈Xx∈X
• e. there isn’t a single element in XX that is “larger” than {g,o,a,d}{g,o,a,d}
• {o,a,f}{o,a,f} is both minimal and maximal because
• {o,a,f}⊉x{o,a,f}⊉x for every x∈Xx∈X
• {o,a,f}⊈x{o,a,f}⊈x for every x∈Xx∈X
• {d,o,g}{d,o,g} is neither minimal nor maximal because
• there is an x∈Xx∈X such that x⊆{d,o,g}x⊆{d,o,g}, namely x={d,o}x={d,o}
• there is an x∈Xx∈X such that {d,o,g}⊆x{d,o,g}⊆x, namely x={g,o,a,d}x={g,o,a,d}
• XX has NEITHER a maximum or a minimum because
• there is no M∈XM∈X such that x⊆Mx⊆M for everyx∈Xx∈X
• there is no m∈Xm∈X such that m⊆xm⊆x for everyx∈Xx∈X

Let’s now relate our discussion above to ring theory. One defines an ideal MM in a ring RR to be a maximal ideal if M≠RM≠R and the only ideal that contains MM is either MM or RR itself, i.e. if I⊴RI⊴R is an  ideal such that M⊆I⊆RM⊆I⊆R, then we must have either I=MI=M or I=RI=R.

Not surprisingly, this coincides with the definition of maximality above. We simply let XX be the set of all proper ideals in the ring RR endowed with the partial order of inclusion ⊆⊆. The only difference is that in this context, because we’re in a ring, we have the second option I=RI=R.

I think a good way to see maximal ideals in action is in the proof of this result:

As a final remark, the notions of “a maximal element” and “an upper bound” come together in Zorn’s Lemma which is needed to prove that every proper ideal in a ring is contained in a maximal ideal. I should mention that an upper bound BB on a partially ordered set (a.k.a. a “poset”) has the same definition as the maximum EXCEPT that BB is not required to be inside the set. More precisely, we define an upper bound on a subset YY of XX to be an element B∈XB∈X such that y≤By≤B for every y∈Yy∈Y.

So here’s the deal with Zorn’s Lemma: It’s not too hard to prove that every finite poset has a maximal element. But what if we don’t know if the given poset is finite? Or what happens if it’s infinite? How can we tell if it has a maximal element? Zorn’s Lemma answers that question:

‍As I mentioned above, it’s this result which is needed to prove that every proper ideal is contained in a maximal ideal***. It actually implies a weaker statement, called Krull’s Theorem (1929), which says that every non-zero ring with unity contains a maximal ideal.

‍Footnotes

*One can easily show that if a set has a maximum it must be unique, hence THE maximum.

** Here’s the proof: Let (X,≤)(X,≤) be a totally ordered set and let m∈Xm∈X be a maximal element. It suffices to show mm is the maximum. Since XX has a total order, either m≤xm≤x or x≤mx≤m for every x∈Xx∈X. If the latter, then mm is the maximum. If the former, then m=xm=x by definition of maximal. In either case, we have x≤mx≤m for all x∈Xx∈X. Hence mm is the maximum.

*** Note this is NOT the same as saying that every maximal ideal contains all the proper ideals in a ring! Remember, maximal ≠≠ maximum!!

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*

This post is the fourth example in an ongoing list of various sequences of functions which converge to different things in different ways.

Also in this series:

Example 1: converges almost everywhere but not in L1L1
Example 2: converges uniformly but not in L1L1
Example 3: converges in L1L1 but not uniformly
Example 5: converges pointwise but not in L1L1
Example 6: converges in L1L1 but does not converge anywhere

Example 4

A sequence of (Lebesgue) integrable functions fn:R→[0,∞)fn:R→[0,∞) so that {fn}{fn} converges to f:R→[0,∞)f:R→[0,∞) uniformly,  yet ff is not (Lebesgue) integrable.

‍Our first observation is that “ff is not (Lebesgue) integrable” can mean one of two things: either ff is not measurable or ∫f=∞∫f=∞. The latter tends to be easier to think about, so we’ll do just that. Now what function do you know of such that when you “sum it up” you get infinity? How about something that behaves like the divergent geometric series? Say, its continuous cousin f(x)=1xf(x)=1x? That should work since we know∫R1x=∫∞11x=∞.∫R1x=∫1∞1x=∞.Now we need to construct a sequence of integrable functions {fn}{fn} whose uniform limit is 1x1x. Let’s think simple: think of drawring the graph of f(x)f(x) one “integral piece” at a time. In other words, define:

This works because: It makes sense to define the fnfn as  f(x)=1xf(x)=1x “chunk by chunk” since this way the convergence is guaranteed to be uniform. Why? Because how far out we need to go in the sequence so that the difference f(x)−fn(x)f(x)−fn(x) is less than ϵϵ only depends on how small (or large) ϵϵ is. The location of xx doesn’t matter!

Also notice we have to define fn(x)=0fn(x)=0 for all x<1x<1 to avoid the trouble spot ln(0)ln⁡(0) in the integral ∫fn∫fn. This also ensures that the area under each fnfn is finite, guaranteeing integrability.

The details: Each fnfn is integrable since for a fixed nn,∫Rfn=∫n11x=ln(n).∫Rfn=∫1n1x=ln⁡(n).To see fn→ffn→f uniformly, let ϵ>0ϵ>0 and choose NN so that N>1/ϵN>1/ϵ. Let x∈Rx∈R. If x≤1x≤1, any nn will do, so suppose x>1x>1 and let n>Nn>N. If 1<x≤n1<x≤n, then we have |fn(x)−f(x)|=0<ϵ|fn(x)−f(x)|=0<ϵ. And if x>nx>n, then∣∣1xχ[1,∞)(x)−1xχ[1,n](x)∣∣=∣∣1x−0∣∣=1x<1n<1N<ϵ.|1xχ[1,∞)(x)−1xχ[1,n](x)|=|1x−0|=1x<1n<1N<ϵ.

‍For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*

 

This post is the third example in an ongoing list of various sequences of functions which converge to different things in different ways.

‍Example 3

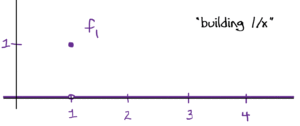
A sequence of continuous functions {fn:R→[0,∞)}{fn:R→[0,∞)} which converges to 0 in the L1L1 norm, but does not converge to 0 uniformly.

There are four criteria we want our functions to satisfy:

1. First off is the uniform convergence. Observe that “{fn}{fn} does not converge to 0 uniformly” can mean one of three things:

• converges to 0 pointwise only
• converges to something other than 0 (pointwise or uniformly)
• does not converge at all

So it’s up to you to decide which one feels more comfortable to work with. Here we’ll choose the second option.

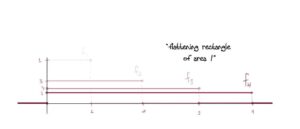
2. Next, “{fn}{fn} converges to 0 in the L1L1 norm” means that we want to choose our sequence so that the area under the curve of the fnfn gets smaller and smaller as n→∞n→∞.
3. Further, we also want the fnfn to be positive (the image of each fnfn must be [0,∞)[0,∞)) (notice this allows us to remove the abosolute value sign in the L1L1 norm: ∫|fn|⇒∫fn∫|fn|⇒∫fn)
4. Lastly, the functions must be continuous.

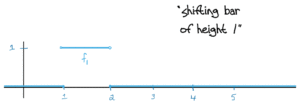
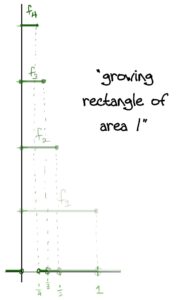
A slick* but very simple solution is a sequence of triangles of decreasing area with height 1!

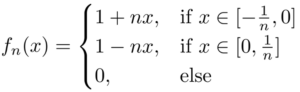
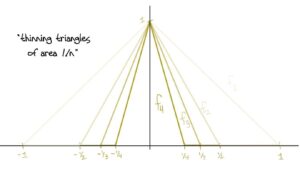
This works because: At x=0x=0, fn(x)=1fn(x)=1 for all nn, so there’s no way it can converge to zero (much less uniformly). In fact we have fn→ffn→f pointwise wheref(x)={1,if x=00otherwise.f(x)={1,if x=00otherwise.The area of each triangle is 1n1n which clearly goes to zero for nn large. Also, it’s clear to see visually that the area is getting smaller. This guarantees fn→0fn→0 in the L1L1 norm. Further, each fnfn is positive since we’ve defined it to equal zero as soon as the edges of the triangle reach the xx-axis. And lastly we have piecewise continuity.

The details: Let ϵ>0ϵ>0 and x∈Rx∈R. If x=0x=0, then fn(x)=1fn(x)=1 for all n and so fn→1fn→1. Otherwise x>0x>0 or x<0x<0 If x>0x>0 and x>1x>1, then fn(x)=0fn(x)=0 for all nn. Otherwise if x∈(0,1]x∈(0,1] choose N>1xN>1x. Then whenever n>Nn>N we have fn(x)=1−nx<1−1xx=0<ϵ.fn(x)=1−nx<1−1xx=0<ϵ. The case when x<0x<0 follows a similar argument.

Lastly fn→0fn→0 in the L1L1 norm since, as we mentioned, the areas are decreasing to 0. Explicitly:  ∫R|fn|=∫0−1n1+nx+∫1n01−nx=2n→0.∫R|fn|=∫−1n01+nx+∫01n1−nx=2n→0.

‍*I can brag because this particular example came from a friend. My own attempt at a solution was not nearly as intuitive.

Constructing the Tensor Product of Modules

The Basic Idea

Today we talk tensor products. Specifically this post covers the construction of the tensor product between two modules over a ring. But before jumping in, I think now’s a good time to ask, “What are tensor products good for?” Here’s a simple example where such a question might arise:

Suppose you have a vector space VV over a field FF. For concreteness, let’s consider the case when VV is the set of all 2×22×2 matrices with entries in RR and let F=RF=R. In this case we know what “FF-scalar multiplication” means: if M∈VM∈V is a matrix and c∈Rc∈R, then the new matrix cMcM makes perfect sense. But what if we want to multiply MM by complex scalars too? How can we make sense of something like (3+4i)M(3+4i)M? That’s precisely what the tensor product is for! We need to create a set of elements of the form(complex number) “times” (matrix)(complex number) “times” (matrix)so that the mathematics still makes sense. With a little massaging, this set will turn out to be C⊗RVC⊗RV.

So in general, if FF is  an arbitrary field and VV an FF-vector space, the tensor product answers the question “How can I define scalar multiplication by some larger field which contains FF?” And of course this holds if we replace the word “field” by “ring” and consider the same scenario with modules.

Now this isn’t the only thing tensor products are good for (far from it!), but I think it’s the most intuitive one since it is readily seen from the definition (which is given below).

So with this motivation in mind, let’s go!

‍From English to Math

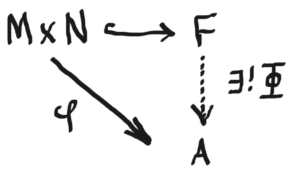
Let RR be a ring with 1 and let MM be a right RR-module and NN a left RR-module and suppose AA is any abelian group. Our goal is to create an abelian group M⊗RNM⊗RN, called the tensor product of MM and NN, such that if there is an RR-balanced map i:M×N→M⊗RNi:M×N→M⊗RN and any RR-balanced map φ:M×N→Aφ:M×N→A, then there is a unique abelian group homomorphism Φ:M⊗RN→AΦ:M⊗RN→A such that φ=Φ∘iφ=Φ∘i, i.e. so the diagram below commutes.

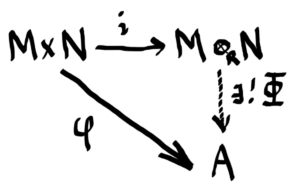
Notice that the statement above has the same flavor as the universal mapping property of free groups!

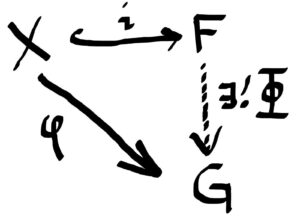
Definition: Let XX be a set. A group FF is said to be a free group on XX if there is a function i:X→Fi:X→F such that for any group GG and any set map φ:X→Gφ:X→G, there exists a unique group homomorphism Φ:F→GΦ:F→G such that the following diagram commutes: (i.e. φ=Φ∘iφ=Φ∘i)

set map, so in particular we just want our’s to be RR-balanced:

: Let RR be a ring with 1. Let MM be a right RR-module, NN a left RR-module, and AA an abelian group. A map φ:M×N→Rφ:M×N→R is called RR-balanced if for all m,m1,m2∈Mm,m1,m2∈M, all n,n1,n2∈Nn,n1,n2∈N and all r∈Rr∈R,
φ(m1+m2,n)=φ(m1,n)+φ(m2,n)φ(m1+m2,n)=φ(m1,n)+φ(m2,n)φ(m,n1+n2)=φ(m,n1)+φ(m,n2)φ(m,n1+n2)=φ(m,n1)+φ(m,n2)φ(mr,n)=φ(m,rn)φ(mr,n)=φ(m,rn)

By “replacing” F by a certain quotient group F/HF/H! (We’ll define HH precisely below.)
These observations give us a road map to construct the tensor product. And so we begin:

‍Step 1

Let FF be a free abelian group generated by M×NM×N and let AA be an abelian group. Then by definition (of free groups), if φ:M×N→Aφ:M×N→A is any set map, and M×N↪FM×N↪F by inclusion, then there is a unique abelian group homomorphism Φ:F→AΦ:F→A so that the following diagram commutes.

Step 2

that the inclusion map M×N↪FM×N↪F is not RR-balanced! To fix this, we must “modify” the target space FF by replacing it with the quotient F/HF/H where H≤FH≤F is the subgroup of FF generated by elements of the form

(m1+m2,n)−(m1,n)−(m2,n)(m1+m2,n)−(m1,n)−(m2,n)

• (m,n1+n2)−(m,n1)−(m,n2)(m,n1+n2)−(m,n1)−(m,n2)
• (mr,n)−(m,rn)(mr,n)−(m,rn)

where m1,m2,m∈Mm1,m2,m∈M, n1,n2,n∈Nn1,n2,n∈N and r∈Rr∈R. Why elements of this form? Because if we define the map i:M×N→F/Hi:M×N→F/H byi(m,n)=(m,n)+H,i(m,n)=(m,n)+H,we’ll see that ii is indeed RR-balanced! Let’s check:

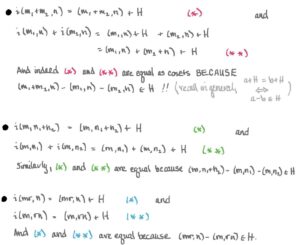
So, are we done now? Can we really just replace FF with F/HF/H and replace the inclusion map with the map ii, and still retain the existence of a unique homomorphism Φ:F/H→AΦ:F/H→A? No! Of course not. F/HF/H is not a free group generated by M×NM×N, so the diagram below is bogus, right?

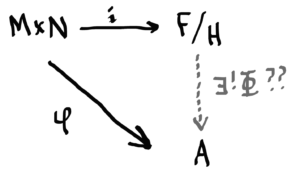
Not totally. We haven’t actually disturbed any structure!

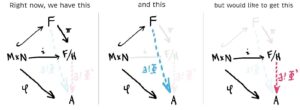
How can we relate the pink and blue lines? We’d really like them to be the same. But we’re in luck because they basically are!

‍Step 3

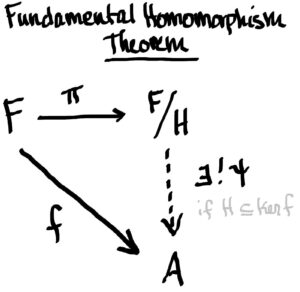
H⊆ker(f)H⊆ker⁡(f), that is as long as f(h)=0f(h)=0 for all h∈Hh∈H. And notice that this condition, f(H)=0f(H)=0, forces ff to be RR-balanced!

Let’s check:

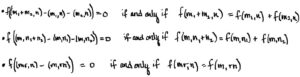
Sooooo… homomorphisms f:F→Af:F→A such that H⊆ker(f)H⊆ker⁡(f) are the same as RR-balanced maps from M×NM×N to AA! (Technically, I should say homomorphisms ff restricted to M×NM×N.) In other words, we have

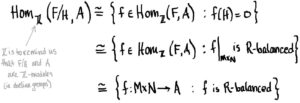
In conclusion, to say “abelian group homomorphisms from F/HF/H to AA are the same as (isomorphic to) RR-balanced maps from M×NM×N to AA” is the simply the hand-wavy way of saying

Whenever i:M×N→Fi:M×N→F is an RR-balanced map and φ:M×N→Aφ:M×N→A is an RR-balanced map where AA is an abelian group, there exists a unique abelian group homomorphism Φ:F/H→AΦ:F/H→A such that the following diagram commutes:

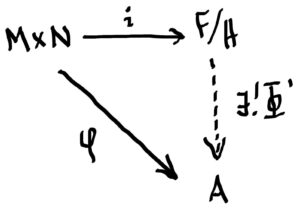
And this is just want we want! The last step is merely the final touch:

‍Step 4

the abelian quotient group F/HF/H to be the tensor product of MM and NN,

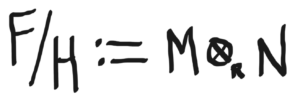
whose elements are cosets,

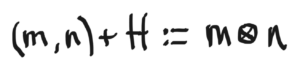
where m⊗nm⊗n for m∈Mm∈M and n∈Nn∈N is referred to as a simple tensor. And there you have it! The tensor product, constructed.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*

This post is the second example in an ongoing list of various sequences of functions which converge to different things in different ways.

‍Example 2

A sequence of functions {fn:R→R}{fn:R→R} which converges to 0 uniformly but does not converge to 0 in L1L1.

This works because:  The sequence tends to 0 as n→∞n→∞ since the height of each function tends to 0 and the the region where fnfn is taking on this decreasing height is tending towards all of R+R+ ((0,n)(0,n) as n→∞n→∞) (and it’s already 0 on R−∪{0}R−∪{0}). The convergence is uniform because the number of times we have to keep “squishing” the rectangles until their height is less than ϵϵ does not depend on xx.

The details: Let ϵ>0ϵ>0 and choose N∈NN∈N so that N>1ϵN>1ϵ and let n>Nn>N. Fix x∈Rx∈R.

Case 1 (x≤0x≤0 or x≥nx≥n) Then fn(x)=0fn(x)=0 and so |fn(x)−0|=0<ϵ|fn(x)−0|=0<ϵ.

• Case 2 (0<x<n0<x<n ) Then fn(x)=1nfn(x)=1n and so |fn(x)−0|=1n<1N<ϵ|fn(x)−0|=1n<1N<ϵ

Finally, fn↛0fn↛0 in L1L1 since∫R|fn|=∫(0,n)1n=1nλ((0,n))=1.∫R|fn|=∫(0,n)1n=1nλ((0,n))=1.

‍Remark: Here’s a question you could ask: wouldn’t fn=nχ(0,1n)fn=nχ(0,1n) work here too? Both are tending to 0 everywhere and both involve rectangles of area 1. The answer is “kinda.” The problem is that the convergence of nχ(0,1n)nχ(0,1n) is pointwise. BUT Egoroff’s Theorem gives us a way to actually “make” it uniform!.

‍On the notation above:   For a measurable set X⊂RX⊂R, denote the set of all Lebesgue integrable functions f:X→Rf:X→R by L1(X)L1(X). Then a sequence of functions {fn}{fn} is said to converge in L1L1  to a function ff if limn→∞∫|fn−f|=0limn→∞∫|fn−f|=0.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*

 

Given a sequence of real-valued functions {fn}{fn}, the phrase, “fnfn converges to a function ff” can mean a few things:

• fnfn converges uniformly
• fnfn converges pointwise
• fnfn converges almost everywhere (a.e.)
• fnfn converges in L1L1 (set of Lebesgue integrable functions)
• and so on…

Other factors come into play if the fnfn are required to be continuous, defined on a compact set, integrable, etc.. So since I do not have the memory of an elephant (whatever that phrase means…), I’ve decided to keep a list of different sequences that converge (or don’t converge) to different functions in different ways. With each example I’ll also include a little (and hopefully) intuitive explanation for why. Having these sequences close at hand is  especially useful when analysing the behavior of certain functions or constructing counterexamples.

The first sequence we’ll look at is one which converges almost everywhere, but does not converge in L1L1 (the set of Lebesgue integrable functions).

‍Example 1

A sequence of functions {fn:R→R}{fn:R→R} which converges to 0 almost everywhere but does not converge to 0 in L1L1.       

This works because: Recall that to say fn→0fn→0 almost everywhere means fn→0fn→0 pointwise on RR except for a set of measure 0. Here, the set of measure zero is the singleton set {0}{0} (at x=0x=0, fn(x)=nfn(x)=n and we can’t make this less than ϵϵ for any ϵ>0ϵ>0). So fnfn converges to 0 pointwise on (0,1](0,1]. This holds because if x<0x<0 or x>1x>1 then fn(x)=0fn(x)=0 for all nn. Otherwise, if x∈(0,1]x∈(0,1], we can choose nn appropriately:

The details:  Let ϵ>0ϵ>0 and x∈(0,1]x∈(0,1] and choose N∈NN∈N so that N>1xN>1x. Then whenever n>Nn>N, we have n>1xn>1x which implies x>1nx>1n and so fn(x)=0fn(x)=0. Hence |fnx−0|=0<ϵ|fnx−0|=0<ϵ.

Further*, fn↛0fn↛0 in L1L1 since∫R|fn|=∫[0,1n]n=nλ([0,1n])=1.∫R|fn|=∫[0,1n]n=nλ([0,1n])=1.

Remark: Notice that Egoroff’s theorem applies here! We just proved that fn→0fn→0 pointwise a.e. on RR, but Egoroff says that we can actually get uniform convergence a.e. on a bounded subset of RR, say (0,1](0,1].

In particular for each ϵ>0ϵ>0 we are guaranteed the existence of a subset E⊂(0,1]E⊂(0,1] such that fn→0fn→0 uniformly and λ((0,1]∖E)<ϵλ((0,1]∖E)<ϵ. In fact, it should be clear that that subset must be something like (ϵ2,1](ϵ2,1] (the “zero region” in the graph above). Then no matter where xx is in (0,1](0,1], we can always find nn large enough – namely all nn which satisfy 1n<ϵ21n<ϵ2 – so that fn(x)=0fn(x)=0, i.e. fn→ffn→f uniformly. And indeed, λ((0,1]∖(ϵ2,1]=ϵ/2<ϵλ((0,1]∖(ϵ2,1]=ϵ/2<ϵ as claimed.

‍On the notation above:   For a measurable set X⊂RX⊂R, denote the set of all Lebesgue integrable functions f:X→Rf:X→R by L1(X)L1(X). Then a sequence of functions {fn}{fn} is said to converge in L1L1  to a function ff if limn→∞∫|fn−f|=0limn→∞∫|fn−f|=0.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*

In any area of math, it’s always good idea to keep a few counterexamples in your back pocket. Examples/non-examples from some of the different subsets of integral domains.

Z[i√5]Z[i5] is an integral domain which is not a UFD

That Z[i√5]Z[i5] an integral domain is easy to check (just computation).

• It’s not a UFD since we can write 6=2⋅3=(1+i√5)(1−i√5)6=2⋅3=(1+i5)(1−i5) as two distinct facorizations into irreducibles*

‍Z[x]Z[x] is a UFD which is not a PID

We know Z[x]Z[x] is a UFD because ZZ is a UFD (recall, a commutative ring RR is a UFD iff R[x]R[x] is a UFD).

• The ideal (2,x)={2f(x)+xg(x):f(x),g(x)∈Z[x]}(2,x)={2f(x)+xg(x):f(x),g(x)∈Z[x]} (polynomials with even constant term) is not principal**

‍Z[12+i√192]Z[12+i192] is a PID which is not a Euclidean domain

• This is a PID since it has a Dedekind-Hasse norm (see Dummit and Foote, 3rd ed., §8.2§8.2).
• It is not a Euclidean domain since it has no universal side divisors (ibid.).

ZZ is a Euclidean domain which is not a field

ZZ is a Euclidean domain via the absolute value norm (which gives the familiar division algorithm).

• It is not a field since the only elements which are units are 11 and −1−1.

‍  (*) Check 2,3,1+i√52,3,1+i5, and 1−i√51−i5 are indeed irreducible in Z[i√5]Z[i5]:

Write 2=αβ2=αβ for α,β∈Z[i√5]α,β∈Z[i5]. Then α=a+ib√5α=a+ib5 and N(α)=a2+5b2N(α)=a2+5b2 for some integers a,ba,b. Since 4=N(2)=N(α)N(β)4=N(2)=N(α)N(β), we must have a2+5b2=1,2a2+5b2=1,2 or 44. Notice b=0b=0 must be true (since a2+5b2∉{1,2,4}a2+5b2∉{1,2,4} for b≥1b≥1 and for any aa). Hence either α=a=1α=a=1 or 22. If α=1α=1 then αα is a unit. If α=2α=2, then we must have β=1β=1 and so ββ is a unit.

• Showing 3 is irreducible follows a similar argument.

‍Write 1+i√5=αβ1+i5=αβ with α=a+ib√5α=a+ib5 so that N(α)=a2+5b2∈{1,2,3,6}N(α)=a2+5b2∈{1,2,3,6} since 6=N(α)N(β)6=N(α)N(β). Consider two cases:  (case 1) If b=0b=0, then a2∈{1,2,3,6}a2∈{1,2,3,6} which is only true if a2=1a2=1 and so α=a=±1α=a=±1 is a unit. (case 2) If b>0b>0, we can only have b2=1b2=1 (since b2>1b2>1 gives a contradiction), and so a2+5∈{1,2,3,6}a2+5∈{1,2,3,6}, which implies a2=1a2=1. Hence α=±1±i√5α=±1±i5 and so N(α)=6N(α)=6. This implies N(β)=1N(β)=1 and so β=±1β=±1, which is a unit.

‍Showing 1−i√51−i5 is irreducible follows a similar argument.

principal in Z[x]Z[x]:

• Suppose to the contrary (2,x)=(f(x))(2,x)=(f(x)) for some polynomial f(x)∈Z[x]f(x)∈Z[x]. Since 2∈(f(x))2∈(f(x)), we must have 2=f(x)p(x)2=f(x)p(x) for some p(x)∈Z[x]p(x)∈Z[x]. Hence 0=degf(x)+degp(x)0=deg⁡f(x)+deg⁡p(x) which implies both f(x)f(x) and p(x)p(x) are constants. In particular, since 2=±1⋅±22=±1⋅±2, we need f(x),p(x)∈{±1,±2}f(x),p(x)∈{±1,±2}. If f(x)=±1f(x)=±1, then (f(x))=Z[x](f(x))=Z[x] which is a contradiction since (f(x))=(2,x)(f(x))=(2,x) mustbe a proper ideal (not every polynomial over Z[x]Z[x] has even constant term). It follows that f(x)=±2f(x)=±2. But since x∈(f(x))x∈(f(x)) as well, x=2r(x)x=2r(x) for some r(x)∈Z[x]r(x)∈Z[x]. But of course this is impossible for any polynomial with integer coefficients, r(x)r(x). Thus (2,x)(2,x) is not principal.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*

 

Here is a list of some of the subsets of integral domains, along with the reasoning (a.k.a proofs) of why the bullseye below looks the way it does. Part 2 of this post will include back-pocket examples/non-examples of each.

Integral Domain: a commutative ring with 1 where the product of any two nonzero elements is always nonzero

Unique Factorization Domain (UFD): an integral domain where every nonzero element (which is not a unit) has a unique factorization into irreducibles

Principal Ideal Domain (PID): an integral domain where every ideal is generated by exactly one element

Euclidean Domain: an integral domain RR with a norm NN and a division algorithm (i.e. there is a norm NN so that for every a,b∈Ra,b∈R with b≠0b≠0, there are q,r∈Rq,r∈R so that a=bq+ra=bq+r with r=0r=0 or N(r)<N(b)N(r)<N(b))

Field: a commutative ring where every nonzero element has an inverse

Because… We can just choose the zero norm: N(r)=0N(r)=0 for all r∈Fr∈F.

Proof: Let FF be a field and define a norm NN so that N(r)=0N(r)=0 for all r∈Fr∈F. Then for any a,b∈Fa,b∈F with b≠0b≠0, we can writea=b(b−1a)+0.a=b(b−1a)+0.

Because… If I◃RI◃R is an arbitrary nonzero ideal in the Euclidean domain RR, then I=(d)I=(d), where d∈Id∈I such that dd has the smallest norm among all elements in II. Prove this using the division algorithm on dd and some a∈Ia∈I.

Proof: Let RR be a Euclidean domain with respect to the norm NN and let I◃RI◃R be an ideal. If I=(0)I=(0), then II is principle. Otherwise let d∈Id∈I be a nonzero element such that dd has the smallest norm among all elements in II. We claim I=(d)I=(d). That (d)⊂I(d)⊂I is clear so let a∈Ia∈I. Then by the division algorithm, there exist q,r∈Rq,r∈R so that a=dq+ra=dq+r with r=0r=0 or N(r)<N(d)N(r)<N(d). Then r=a−dq∈Ir=a−dq∈I since a,d∈Ia,d∈I. But my minimality of dd, this implies r=0r=0. Hence a=dq∈(d)a=dq∈(d) and so I⊂(d)I⊂(d).

Because…Every PID has the ascending chain condition (acc) on its ideals!* So to prove PID ⇒⇒ UFD, just recall that an integral domain RR is a UFD if and only if 1) it has the acc on principal ideals** and 2) every irreducible element is also prime.

Proof: Let RR be a PID. Then 1) RR has the ascending chain condition on principal ideals and 2) every irreducible element is also a prime element. Hence RR is a UFD.

Because… By definition.

Proof: By definition.

‍*Def: In general, an integral domain RR has the acc on its principal ideals if these two equivalent conditions are satisfied:

1. Every sequence I1⊂I2⊂⋯⊂⋯I1⊂I2⊂⋯⊂⋯ of principal ideals is stationary (i.e. there is an integer n0≥1n0≥1 such that In=In0In=In0 for all n≥n0n≥n0).
2. For every nonempty subset X⊂RX⊂R, there is an element m∈Xm∈X such that whenever a∈Xa∈X and (m)⊂(a)(m)⊂(a), then (m)=(a)(m)=(a).

**To see this, use part 1 of the definition above. If I1⊂I2⊂⋯I1⊂I2⊂⋯ is an acsending chain, consider their union I=⋃∞n=1InI=⋃n=1∞In. That guy must be a principal ideal (check!), say I=(m)I=(m). This implies that mm must live in some In0In0  for some n0≥1n0≥1 and so I=(m)⊂In0I=(m)⊂In0. But since II is the union, we have for all n≥n0n≥n0(m)=I⊃In⊃In0=(m).(m)=I⊃In⊃In0=(m).Voila!

Every field FF is a PID

because the only ideals in a field are (0)(0) and F=(1)F=(1)! And every field is vacuously a UFD since all elements are units. (Recall, RR is a UFD if every non-zero, non-invertible element (an element which is not a unit) has a unique factorzation into irreducibles).

‍In an integral domain, every maximal ideal is also a prime ideal. 

(Proof: Let RR be an integral domain and M◃RM◃R a maximal ideal. Then R/MR/M is a field and hence an integral domain, which implies M◃RM◃R is a prime ideal.)

Butut the converse is not true (see counterexample below). However, the converse is true in a PID because of the added structure!

(Proof: Let RR be a PID and (p)◃R(p)◃R a prime ideal for some p∈Rp∈R. Then pp is a prime – and hence an irreducible – element (prime ⇔⇔ irreducible in PIDs). Since in an integral domain a principal ideal is maximal whenever it is generated by an irreducible element, we conclude (p)(p) is maximal.)

This suggests that if you want to find a counterexample – an integral domain with a prime ideal which is not maximal – try to think of a ring which is not a PID:   In Z[x]Z[x], consider the ideal (p)(p) for a prime integer pp. Then (p)(p) is a prime ideal, yet it is not maximal since(p)⊂(p,x)⊂Z[x].(p)⊂(p,x)⊂Z[x].

‍If FF is a field, then F[x]F[x] – the ring of polynomials in xx with coefficients in FF – is a Euclidean domain with the norm N(p(x))=degp(x)N(p(x))=deg⁡p(x) where p(x)∈F[x]p(x)∈F[x].

By the integral domain hierarchy above, this implies every ideal in F[x]F[x] is of the form (p(x))(p(x)) (i.e. F[x]F[x] is a PID) and every polynomial can be factored uniquely into a product of prime polynomials (just like the integers)! The next bullet gives an “almost converse” statement.

‍If R[x]R[x] is a PID, the RR must be a field.

To see this, simply observe that R⊂R[x]R⊂R[x] and so RR must be an integral domain (since a subset of a integral domain inherets commutativity and the “no zero divisors” property). Since R[x]/(x)≅RR[x]/(x)≅R, it follows that R[x]/(x)R[x]/(x) is also an integral domain. This proves that (x)(x) is a prime ideal. But prime implies maximal in a PID! So R[x]/(x)R[x]/(x) – and therefore RR – is actually a field.

• This is how we know, for example, that Z[x]Z[x] is not a PID (in the counterexample a few bullets up) – ZZ is not a field!

‍For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*

Bob Moses, who helped register Black residents to vote in Mississippi during the Civil Rights Movement, believed civil rights went beyond the ballot box. To Moses, who was a teacher as well as an activist, math literacy is a civil right: a requirement to earning a living wage in modern society. In 1982, he founded the Algebra Project to ensure that “students at the bottom get the math literacy they need.”

As a researcher who studies ways to improve the math experiences of students, we believe a new approach that expands access to algebra may help more students get the math literacy Moses, who died in 2021, viewed as so important. It’s a goal districts have long been struggling to meet.

Efforts to improve student achievement in algebra have been taking place for decades. Unfortunately, the math pipeline in the United States is fraught with persistent opportunity gaps. According to the Nation’s Report Card—a congressionally mandated project administered by the Department of Education—in 2022 only 29% of U.S. fourth graders and 20% of U.S. eighth graders were proficient in math. Low-income students, students of colour and multilingual learners, who tend to have lower scores on math assessments, often do not have the same access as others to qualified teachers, high-quality curriculum and well-resourced classrooms.

A new approach

The Dallas Independent School District—or Dallas ISD—is gaining national attention for increasing opportunities to learn by raising expectations for all students. Following in the footsteps of more than 60 districts in the state of Washington, in 2019 the Dallas ISD implemented an innovative approach of having students be automatically enrolled rather than opt in to honours math in middle school.

Under an opt-in policy, students need a parent or teacher recommendation to take honours math in middle school and Algebra 1 in eighth grade. That policy led both to low enrolment and very little diversity in honours math. Some parents, especially those who are Black or Latino, were not aware how to enroll their students in advanced classes due to a lack of communication in many districts.

In addition, implicit bias, which exists in all demographic groups, may influence teachers’ perceptions of the behaviour and academic potential of students, and therefore their subsequent recommendations. Public school teachers in the U.S. are far less racially and ethnically diverse than the students they serve.

Dallas ISD’s policy overhaul aimed to foster inclusivity and bridge educational gaps among students. Through this initiative, every middle school student, regardless of background, was enrolled in honours math, the pathway that leads to taking Algebra 1 in eighth grade, unless they opted out.

Flipping the switch from opt-in to opt-out led to a dramatic increase in the number of Black and Latino learners, who constitute the majority of Dallas students. And the district’s overall math scores remained steady. About 60% of Dallas ISD eighth graders are now taking Algebra 1, triple the prior level. Moreover, more than 90% are passing the state exam.

Efforts spread

Other cities are taking notice of the effects of Dallas ISD’s shifting policy. The San Francisco Unified School District, for example, announced plans in February 2024 to implement Algebra 1 in eighth grade in all schools by the 2026-27 school year.

In fall 2024, the district will pilot three programs to offer Algebra 1 in eighth grade. The pilots range from an opt-out program for all eighth graders—with extra support for students who are not proficient—to a program that automatically enrolls proficient students in Algebra 1, offered as an extra math class during the school day. Students who are not proficient can choose to opt in. Nationwide, however, districts that enroll all students in Algebra 1 and allow them to opt out are still in the minority. And some stopped offering eighth grade Algebra 1 entirely, leaving students with only pre-algebra classes. Cambridge, Massachusetts—the city in which Bob Moses founded the Algebra Project—is among them.

Equity concerns linger

Between 2017 and 2019, district leaders in the Cambridge Public Schools phased out the practice of placing middle school students into “accelerated” or “grade-level” math classes. Few middle schools in the district now offer Algebra 1 in eighth grade.

The policy shift, designed to improve overall educational outcomes, was driven by concerns over significant racial disparities in advanced math enrollment in high school. Completion of Algebra 1 in eighth grade allows students to climb the math ladder to more difficult classes, like calculus, in high school. In Cambridge, the students who took eighth grade Algebra 1 were primarily white and Asian; Black and Latino students enrolled, for the most part, in grade-level math.

Some families and educators contend that the district’s decision made access to advanced math classes even more inequitable. Now, advanced math in high school is more likely to be restricted to students whose parents can afford to help them prepare with private lessons, after-school programs or private schooling, they said.

While the district has tried to improve access to advanced math in high school by offering a free online summer program for incoming ninth graders, achievement gaps have remained persistently wide.

Perhaps striking a balance between top-down policy and bottom-up support will help schools across the U.S. realize the vision Moses dreamed of in 1982 when he founded the Algebra Project: “That in the 21st century every child has a civil right to secure math literacy—the ability to read, write and reason with the symbol systems of mathematics.”

For more insights like this, visit our website at www.international-maths-challenge.com.

Credit of the article given to Liza Bondurant, The Conversation

 

 

These are painful times for those hoping to see an international consensus and substantive action on global warming.

In the US, Republican presidential front-runner Mitt Romney said in June 2011: “The world is getting warmer” and “humans have contributed” but in October 2011 he backtracked to: “My view is that we don’t know what’s causing climate change on this planet.”

His Republican challenger Rick Santorum added: “We have learned to be sceptical of ‘scientific’ claims, particularly those at war with our common sense” and Rick Perry, who suspended his campaign to become the Republican presidential candidate last month, stated flatly: “It’s all one contrived phony mess that is falling apart under its own weight.”

Meanwhile, the scientific consensus has moved in the opposite direction. In a study published in October 2011, 97% of climate scientists surveyed agreed global temperatures have risen over the past 100 years. Only 5% disagreed that human activity is a significant cause of global warming.

The study concluded in the following way: “We found disagreement over the future effects of climate change, but not over the existence of anthropogenic global warming.

“Indeed, it is possible that the growing public perception of scientific disagreement over the existence of anthropocentric warming, which was stimulated by press accounts of [the UK’s] ”Climategate“ is actually a misperception of the normal range of disagreements that may persist within a broad scientific consensus.”

More progress has been made in Europe, where the EU has established targets to reduce emissions by 20% (from 1990 levels) by 2020. The UK, which has been beset by similar denial movements, was nonetheless able to establish, as a legally binding target, an 80% reduction by 2050 and is a world leader on abatement.

In Australia, any prospect for consensus was lost when Tony Abbott used opposition to the Labor government’s proposed carbon market to replace Malcolm Turnbull as leader of the Federal Opposition in late 2009.

It used to be possible to hear right-wing politicians in Australia or the USA echo the Democratic congressman Henry Waxman who said last year:

“If my doctor told me I had cancer, I wouldn’t scour the country to find someone to tell me that I don’t need to worry about it.”

But such rationality has largely left the debate in both the US and Oz. In Australia, a reformulated carbon tax policy was enacted in November only after a highly partisan debate.

In Canada, the debate is a tad more balanced. The centre-right Liberal government in British Columbia passed the first carbon tax in North America in 2008, but the governing Federal Conservative party now offers a reliable “anti-Kyoto” partnership with Washington.

Overviews of the evidence for global warming, together with responses to common questions, are available from various sources, including:

• Seven Answers to Climate Contrarian Nonsense, in Scientific American
• Climate change: A Guide for the Perplexed, in New Scientist
• Cooling the Warming Debate: Major New Analysis Confirms That Global Warming Is Real, in Science Daily
• Remind me again: how does climate change work? on The Conversation

It should be acknowledged in these analyses that all projections are based on mathematical models with a significant level of uncertainty regarding highly complex and only partially understood systems.

As 2011 Australian Nobel-Prize-winner Brian Schmidt explained while addressing a National Forum on Mathematical Education:

“Climate models have uncertainty and the earth has natural variation … which not only varies year to year, but correlates decade to decade and even century to century. It is really hard to design a figure that shows this in a fair way — our brain cannot deal with the correlations easily.

“But we do have mathematical ways of dealing with this problem. The Australian academy reports currently indicate that the models with the effects of CO₂ are with 90% statistical certainty better at explaining the data than those without.

“Most of us who work with uncertainty know that 90% statistical uncertainty cannot be easily shown within a figure — it is too hard to see …”

“ … Since predicting the exact effects of climate change is not yet possible, we have to live with uncertainty and take the consensus view that warming can cover a wide range of possibilities, and that the view might change as we learn more.”

But uncertainty is no excuse for inaction. The proposed counter-measures (e.g. infrastructure renewal and modernisation, large-scale solar and wind power, better soil remediation and water management, not to mention carbon taxation) are affordable and most can be justified on their own merits, while the worst-case scenario — do nothing while the oceans rise and the climate changes wildly — is unthinkable.

Some in the first world protest that any green energy efforts are dwarfed by expanding energy consumption in China and elsewhere. Sure, China’s future energy needs are prodigious, but China also now leads the world in green energy investment.

By blaiming others and focusing the debate on the level of human responsibility for warming and about the accuracy of predictions, the deniers have managed to derail long-term action in favour of short-term economic policies.

Who in the scientific community is promoting the denial of global warming? As it turns out, the leading figures in this movement have ties to conservative research institutes funded mostly by large corporations, and have a history of opposing the scientific consensus on issues such as tobacco and acid rain.

What’s more, those who lead the global warming denial movement – along with creationists, intelligent design writers and the “mathematicians” who flood our email inboxes with claims that pi is rational or other similar nonsense – are operating well outside the established boundaries of peer-reviewed science.

Austrian-born American physicist Fred Singer, arguably the leading figure of the denial movement, has only six peer-reviewed publications in the climate science field, and none since 1997.

After all, when issues such as these are “debated” in any setting other than a peer-reviewed journal or conference, one must ask: “If the author really has a solid argument, why isn’t he or she back in the office furiously writing up this material for submission to a leading journal, thereby assuring worldwide fame and glory, not to mention influence?”

In most cases, those who attempt to grab public attention through other means are themselves aware they are short-circuiting the normal process, and that they do not yet have the sort of solid data and airtight arguments that could withstand the withering scrutiny of scientific peer review.

When they press their views in public to a populace that does not understand how the scientific enterprise operates, they are being disingenuous.

With regards to claims scientists are engaged in a “conspiracy” to hide the “truth” on an issue such as global warming or evolution, one should ask how a secret “conspiracy” could be maintained in a worldwide, multicultural community of hundreds of thousands of competitive researchers.

As Benjamin Franklin wrote in his Poor Richard’s Almanac: “Three can keep a secret, provided two of them are dead.” Or as one of your present authors quipped, tongue-in-cheek, in response to a state legislator who was skeptical of evolution: “You have no idea how humiliating this is to me — there is a secret conspiracy among leading scientists, but no-one deemed me important enough to be included!”

There’s another way to think about such claims: we have tens-of-thousands of senior scientists in their late-fifties or early-sixties who have seen their retirement savings decimated by the recent stock market plunge. These are scientists who now wonder if the day will ever come when they are financially well-off-enough to do their research without the constant stress and distraction of applying for grants (the majority of which are never funded).

All one of these scientists has to do to garner both worldwide fame and considerable fortune (through book contracts, the lecture circuit and TV deals) is to call a news conference and expose “the truth”. So why isn’t this happening?

The system of peer-reviewed journals and conferences sponsored by major professional societies is the only proper forum for the presentation and debate of new ideas, in any field of science or mathematics.

It has been stunningly successful: errors have been uncovered, fraud has been rooted out and bogus scientific claims (such as the 1903 N-ray claim, the 1989 cold fusion claim, and the more-recent assertion of an autism-vaccination link) have been debunked.

This all occurs with a level of reliability and at a speed that is hard to imagine in other human endeavours. Those who attempt to short-circuit this system are doing potentially irreparable harm to the integrity of the system.

They may enrich themselves or their friends, but they are doing grievous damage to society at large.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Jonathan Borwein (Jon), University of Newcastle and David H. Bailey, University of California, Davis