Author: IMC

Pi defines the relationship between a circle’s radius and its area.

Some people have argued that Pi’s days are numbered and that other tools, such as tau, could do its job more efficiently. As someone who has studied Pi throughout his entire working life, my response to such challenges is unwavering: Pi is the gift that keeps on giving.

People call me Doctor Pi. I have played with Pi since I was a child and have studied it seriously for 30 years. Each year I discover new, unexpected and amusing things about Pi, its history and its computation. I never tire of it.

Erm, what is Pi?

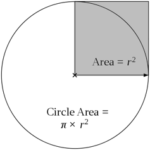
Pi, written with the Greek letter π, has the value of 3.14159 …, is the most important number in mathematics. The area of a circle of radius r is πr² while the perimeter has length 2πr.

Some Pi facts? OK

• Without Pi there is no theory of motion, no understanding of geometry or space/time.
• Pi occurs in important fields of applied mathematics.
• Pi is used throughout engineering, science and medicine and is studied for its own sake in number theory.
• It fascinates specialists and hobbyists alike.

The history of Pi is a history of mathematics

The most famous names in mathematics – Leibniz, Euler, Gauss, Riemann – all play their part in Pi’s illustrious history. In approximately 250BCE Archimedes of Syracuse rigorously showed that the area of a circle is Pi times the square of its radius.

Isaac Newton computed Pi to at least 15 digits in 1666 and a raft of new formulas for calculating Pi in the intervening years have vastly expanded our understanding of this irrational, irreplaceable number.

In my capacity as Doctor Pi – an affectionate name given to me by my students and colleagues – I have met Nobel Prize winners, pop stars and variety of colourful characters, many of whom go potty for this number.

So why the broad attraction? What is the secret of Pi’s enduring appeal? It appears in The Simpsons (doh!), in Star Trek (beam me up!), and in British singer-songwriter Kate Bush’s lovely 2005 song Pi:

“Sweet and gentle and sensitive man With an obsessive nature and deep fascination for numbers And a complete infatuation with the calculation of Pi.”

In the song’s refrain, Bush recites the first 160 digits of Pi (but messes up after 50!) Pi shows up in the movie The Matrix, episodes of Law and Order, and Yann Martel’s Mann-Booker prize winning 2001 novel Life of Pi. No other piece of mathematics can command such attention.

Memorising Pi

The current Guinness World Record for reciting these by rote is well in excess of 60,000 digits.

This is particularly impressive when you consider that Pi, having been proven irrational in the 18th century, has no known repetition or pattern within its infinite decimal representation.

A former colleague of mine, Simon Plouffe, was a Guinness World Record-holder a generation ago, after reciting Pi to approximately 4,700 digits.

Not surprisingly, there is a trend towards building mnemonics whereby the number of letters in a given word represents a digit in the series. For example “How I need a drink, alcoholic of course” represents 3.1415926. This mnemonic formed the basis of a Final Jeopardy! question in 2005.

Some mnemonics are as long as 4,000 digits, but my current favourite is a 33-digit self-referrent mnemonic published in New Scientist on Pi Day (March 14) last year.

Is Pi really infinite?

In a word: yes. So far, it has been calculated to five trillion (5,000,000,000,000) digits. This record was set in August 2010 on Shigeru Kondo’s US$18,000 homemade computer using software written by American university student Alex Yee.

Each such computation is a tour-de-force of computing science.

Estimates suggest that within the next ten to 15 years a quadrillion (1,000,000,000,000,000) digits of Pi will probably be computed. As relatively-recently as 1961, Daniel Shanks, who himself calculated Pi to over 100,000 digits, declared that computing one billion digits would be “forever impossible”. As it transpired, this feat was achieved in 1989 by Yasumasa Kanada of Japan.

It’s a kind of magic

Although it is very likely we will learn nothing new mathematically about Pi from computations to come, we just may discover something truly startling. Pi has seen off attacks in the past. It will see off attacks in the future. Pi, like its inherent magic, is infinite.

The battle continues.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Jonathan Borwein (Jon)*

These are painful times for those hoping to see an international consensus and substantive action on global warming.

In the US, Republican presidential front-runner Mitt Romney said in June 2011: “The world is getting warmer” and “humans have contributed” but in October 2011 he backtracked to: “My view is that we don’t know what’s causing climate change on this planet.”

His Republican challenger Rick Santorum added: “We have learned to be sceptical of ‘scientific’ claims, particularly those at war with our common sense” and Rick Perry, who suspended his campaign to become the Republican presidential candidate last month, stated flatly: “It’s all one contrived phony mess that is falling apart under its own weight.”

Meanwhile, the scientific consensus has moved in the opposite direction. In a study published in October 2011, 97% of climate scientists surveyed agreed global temperatures have risen over the past 100 years. Only 5% disagreed that human activity is a significant cause of global warming.

The study concluded in the following way: “We found disagreement over the future effects of climate change, but not over the existence of anthropogenic global warming.

“Indeed, it is possible that the growing public perception of scientific disagreement over the existence of anthropocentric warming, which was stimulated by press accounts of [the UK’s] ”Climategate“ is actually a misperception of the normal range of disagreements that may persist within a broad scientific consensus.”

More progress has been made in Europe, where the EU has established targets to reduce emissions by 20% (from 1990 levels) by 2020. The UK, which has been beset by similar denial movements, was nonetheless able to establish, as a legally binding target, an 80% reduction by 2050 and is a world leader on abatement.

In Australia, any prospect for consensus was lost when Tony Abbott used opposition to the Labor government’s proposed carbon market to replace Malcolm Turnbull as leader of the Federal Opposition in late 2009.

It used to be possible to hear right-wing politicians in Australia or the USA echo the Democratic congressman Henry Waxman who said last year:

“If my doctor told me I had cancer, I wouldn’t scour the country to find someone to tell me that I don’t need to worry about it.”

But such rationality has largely left the debate in both the US and Oz. In Australia, a reformulated carbon tax policy was enacted in November only after a highly partisan debate.

In Canada, the debate is a tad more balanced. The centre-right Liberal government in British Columbia passed the first carbon tax in North America in 2008, but the governing Federal Conservative party now offers a reliable “anti-Kyoto” partnership with Washington.

Overviews of the evidence for global warming, together with responses to common questions, are available from various sources, including:

• Seven Answers to Climate Contrarian Nonsense, in Scientific American
• Climate change: A Guide for the Perplexed, in New Scientist
• Cooling the Warming Debate: Major New Analysis Confirms That Global Warming Is Real, in Science Daily
• Remind me again: how does climate change work? on The Conversation

It should be acknowledged in these analyses that all projections are based on mathematical models with a significant level of uncertainty regarding highly complex and only partially understood systems.

As 2011 Australian Nobel-Prize-winner Brian Schmidt explained while addressing a National Forum on Mathematical Education:

“Climate models have uncertainty and the earth has natural variation … which not only varies year to year, but correlates decade to decade and even century to century. It is really hard to design a figure that shows this in a fair way — our brain cannot deal with the correlations easily.

“But we do have mathematical ways of dealing with this problem. The Australian academy reports currently indicate that the models with the effects of CO₂ are with 90% statistical certainty better at explaining the data than those without.

“Most of us who work with uncertainty know that 90% statistical uncertainty cannot be easily shown within a figure — it is too hard to see …”

“ … Since predicting the exact effects of climate change is not yet possible, we have to live with uncertainty and take the consensus view that warming can cover a wide range of possibilities, and that the view might change as we learn more.”

But uncertainty is no excuse for inaction. The proposed counter-measures (e.g. infrastructure renewal and modernisation, large-scale solar and wind power, better soil remediation and water management, not to mention carbon taxation) are affordable and most can be justified on their own merits, while the worst-case scenario — do nothing while the oceans rise and the climate changes wildly — is unthinkable.

Some in the first world protest that any green energy efforts are dwarfed by expanding energy consumption in China and elsewhere. Sure, China’s future energy needs are prodigious, but China also now leads the world in green energy investment.

By blaiming others and focusing the debate on the level of human responsibility for warming and about the accuracy of predictions, the deniers have managed to derail long-term action in favour of short-term economic policies.

Who in the scientific community is promoting the denial of global warming? As it turns out, the leading figures in this movement have ties to conservative research institutes funded mostly by large corporations, and have a history of opposing the scientific consensus on issues such as tobacco and acid rain.

What’s more, those who lead the global warming denial movement – along with creationists, intelligent design writers and the “mathematicians” who flood our email inboxes with claims that pi is rational or other similar nonsense – are operating well outside the established boundaries of peer-reviewed science.

Austrian-born American physicist Fred Singer, arguably the leading figure of the denial movement, has only six peer-reviewed publications in the climate science field, and none since 1997.

After all, when issues such as these are “debated” in any setting other than a peer-reviewed journal or conference, one must ask: “If the author really has a solid argument, why isn’t he or she back in the office furiously writing up this material for submission to a leading journal, thereby assuring worldwide fame and glory, not to mention influence?”

In most cases, those who attempt to grab public attention through other means are themselves aware they are short-circuiting the normal process, and that they do not yet have the sort of solid data and airtight arguments that could withstand the withering scrutiny of scientific peer review.

When they press their views in public to a populace that does not understand how the scientific enterprise operates, they are being disingenuous.

With regards to claims scientists are engaged in a “conspiracy” to hide the “truth” on an issue such as global warming or evolution, one should ask how a secret “conspiracy” could be maintained in a worldwide, multicultural community of hundreds of thousands of competitive researchers.

As Benjamin Franklin wrote in his Poor Richard’s Almanac: “Three can keep a secret, provided two of them are dead.” Or as one of your present authors quipped, tongue-in-cheek, in response to a state legislator who was skeptical of evolution: “You have no idea how humiliating this is to me — there is a secret conspiracy among leading scientists, but no-one deemed me important enough to be included!”

There’s another way to think about such claims: we have tens-of-thousands of senior scientists in their late-fifties or early-sixties who have seen their retirement savings decimated by the recent stock market plunge. These are scientists who now wonder if the day will ever come when they are financially well-off-enough to do their research without the constant stress and distraction of applying for grants (the majority of which are never funded).

All one of these scientists has to do to garner both worldwide fame and considerable fortune (through book contracts, the lecture circuit and TV deals) is to call a news conference and expose “the truth”. So why isn’t this happening?

The system of peer-reviewed journals and conferences sponsored by major professional societies is the only proper forum for the presentation and debate of new ideas, in any field of science or mathematics.

It has been stunningly successful: errors have been uncovered, fraud has been rooted out and bogus scientific claims (such as the 1903 N-ray claim, the 1989 cold fusion claim, and the more-recent assertion of an autism-vaccination link) have been debunked.

This all occurs with a level of reliability and at a speed that is hard to imagine in other human endeavours. Those who attempt to short-circuit this system are doing potentially irreparable harm to the integrity of the system.

They may enrich themselves or their friends, but they are doing grievous damage to society at large.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Jonathan Borwein (Jon), University of Newcastle and David H. Bailey, University of California, Davis

Richard Braatz. Photo: Dominick Reuter

Trial-and-error experimentation underlies many biomedical innovations. This classic method — define a problem, test a proposed solution, learn from failure and try again — is the main route by which scientists discover new biomaterials and drugs today. This approach is also used to design ways of manufacturing these new materials, but the process is immensely time-consuming, producing a successful therapeutic product and its manufacturing process only after years of experiments, at considerable expense.

Richard Braatz, the Edwin R. Gilliland Professor of Chemical Engineering at MIT, applies mathematics to streamline the development of pharmaceuticals. Trained as an applied mathematician, Braatz is developing mathematical models to help scientists quickly and accurately design processes for manufacturing drug compounds with desired characteristics. Through mathematical simulations, Braatz has designed a system that significantly speeds the design of drug-manufacturing processes; he is now looking to apply the same mathematical approach to designing new biomaterials and nanoscale devices.

“Nanotechnology is very heavily experimental,” Braatz says. “There are researchers who do computations to gain insights into the physics or chemistry of nanoscale systems, but do not apply these computations for their design or manufacture. I want to push systematic design methods to the nanoscale, and to other areas where such methods aren’t really developed yet, such as biomaterials.”

From farm to formulas

Braatz’s own academic path was anything but systematic. He spent most of his childhood on an Oregon farm owned by his grandfather. Braatz says he absorbed an engineer’s way of thinking early on from his father, an electrician, by examining his father’s handiwork on the farm and reading his electrical manuals.

Braatz also developed a serious work ethic. From the age of 10, he awoke early every morning — even on school days — to work on the farm. In high school, he picked up a night job at the local newspaper, processing and delivering thousands of newspapers to stores and the post office, sometimes until just before dawn.

After graduating from high school in 1984, Braatz headed to Alaska for the summer. A neighbour had told him that work paid well up north, and Braatz took a job at a fish-processing facility, driving forklifts and hauling 100-pound bags of fishmeal 16 hours a day. He returned each summer for four years, eventually working his way up to plant operator, saving enough money each summer to pay for the next year’s tuition at Oregon State University.

As an undergraduate, Braatz first planned to major in electrical engineering. But finding the introductory coursework unstimulating — given the knowledge he’d absorbed from his father — he cast about for another major.

“There was no Internet back then, so you couldn’t Google; web searches didn’t exist,” Braatz says. “So I went to the library and opened an encyclopedia, and said, ‘OK, what other engineering [is] there?’”

Chemical engineering caught his eye; he had always liked and excelled at chemistry in high school. While pursuing a degree in chemical engineering, Braatz filled the rest of his schedule with courses in mathematics.

After graduation, Braatz went on to the California Institute of Technology, where he earned both a master’s and a PhD in chemical engineering. In addition to his research, Braatz took numerous math and math-heavy courses in electrical engineering, applied mechanics, chemical engineering and chemistry. The combination of real applications and mathematical theory revealed a field of study Braatz had not previously considered: applied mathematics.

“This training was a very good background for learning how to derive mathematical solutions to research problems,” Braatz says.

A systems approach

Soon after receiving his PhD, Braatz accepted an assistant professorship at the University of Illinois at Urbana-Champaign (UIUC). There, as an applied mathematician, he worked with researchers to tackle problems in a variety of fields: computer science, materials science, and electrical, chemical and mechanical engineering.

He spent eight years on a project spurred by a talk he attended at UIUC. In that talk, a representative of Merck described a major challenge in the pharmaceutical industry: controlling the size of crystals in the manufacture of any given drug. (The size and consistency of crystals determine, in part, a drug’s properties and overall efficacy.)

Braatz learned that while drug-manufacturing machinery was often monitored by sensors, much of the resulting data went unanalysed. He pored over the sensors’ data, and developed mathematical models to gain an understanding of what the sensors reveal about each aspect of the drug-crystallization process. Over the years, his team devised an integrated series of algorithms that combined efficiently designed experiments with mathematical models to yield a desired crystal size from a given drug solution. They worked the algorithms into a system that automatically adjusts settings at each phase of the manufacturing process to produce an optimal crystal size, based on a “recipe” given by the algorithms.

“Sometimes the recipes are very weird,” Braatz says. “It might be a strange path you have to follow to manufacture the right crystals.”

The automated system, which has since been adopted by Merck and other pharmaceutical companies, provides a big improvement in efficiency, Braatz says, avoiding the time-consuming trial-and-error approach many drug manufacturers had relied on to design a crystallization process for a new drug.

In 2010, Braatz moved to MIT, where he is exploring mathematical applications in nanotechnology and tissue engineering — in particular, models to help design new drug-releasing materials. Such materials have the potential to deliver controlled, continuous therapies, but designing them currently takes years of trial-and-error experiments.

Braatz’s group is designing mathematical models to give researchers instructions, for example, on how to design materials that locally release drugs into a body’s cells at a desired rate. Braatz says approaching such a problem from a systematic perspective could potentially save years of time in the development of a biomedical material of high efficacy.

“Anything is a win if you could reduce those experiments from 10 years to several years,” Braatz says. “We’re talking hundreds of millions, billions of dollars. And the effect on people’s lives, you can’t put a price tag on that.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Jennifer Chu, Massachusetts Institute of Technology

Conventional wisdom says that you should never leave money on the table when negotiating. But research in my field suggests this could be exactly the wrong approach.

There’s mounting evidence that a short-term win at the bargaining table can mean a loss in terms of overall trust and cooperation. That can leave everyone—including the “winner”—worse off.

As a former executive, I’ve managed large contracts as both a buyer and a seller. Now, as a business professor, I study these trading partner relationships, exploring what works in practice. My work supports what economic theorists and social scientists have been arguing for years: The best results come when people collaborate to create long-term value instead of fighting for short-term wins.

What game are you playing?

Research into art, science and practice of collaborative approaches dates back to the 1940s when the mathematician John von Neumann and economist Oskar Morgenstern used mathematical analysis to model competition and cooperation in living things.

Interest in collaborative approaches grew when researchers John Nash, John C. Harsanyi and Reinhard Selten won a Nobel Memorial Prize in Economic Sciences in 1994. Their work inspired academics around the world to delve deeper into what’s known as game theory.

Game theory is the study of the outcome of strategic interactions among decision makers. By using rigorous statistical methods, researchers can model what happens when people choose to cooperate or choose to take an aggressive, power-based approach to negotiation.

Many business leaders are taught strategies focusing on using their power and playing to win—often at the other party’s expense. In game theory, this is known as a zero-sum game, and it’s an easy trap to fall into.

But not every game has a clear winner or loser. In economics, a win-win game is called a nonzero-sum game. In this sort of situation, people aren’t fighting over whose slice of a pie will be larger. They’re working to grow the pie for everyone.

Kate Vitasek lays out five rules for developing a value creation strategy.

A second dimension of game theory is whether people are playing a one-shot or a repeated game. Think of a one-shot game as like going to the flea market: You probably won’t see your trading partner again, so if you’re a jerk to them, the risk of facing the consequences is low.

An interesting twist uncovered by studying repeated games is that when one party uses their power in a negotiation, it creates the urge for the other party to retaliate.

The University of Michigan’s Robert Axelrod, a mathematician turned game theorist, coined this a “tit-for-tat” strategy. His research, perhaps best known in the book “The Evolution of Cooperation,” uses statistics to show that when individuals cooperate, they come out better than when they don’t.

The case for leaving money on the table

Another Nobel laureate, American economist Oliver Williamson, has offered negotiating advice that most would call a paradigm shift—and some, a heresy.

That advice? Always leave money on the table—especially when you’ll be returning to the same “game” again. Why? According to Williamson, it sends a powerful signal of trustworthiness and credibility to one’s negotiating partner when someone consciously chooses to cooperate and build trust.

The opposite approach leads to lost trust and what the Nobel laureate economist Oliver Hart calls “shading.” This is a retaliatory behaviour that happens when a party isn’t getting the outcome it expected from a deal and feels the other party is to blame.

Simply put, noncollaborative approaches causes distrust and create friction, which adds transaction costs and inefficiencies.

The million-dollar question is whether collaborative approaches work in practice. And from my vantage point as a scholar, the answer is yes. In fields as diverse as health care to high-tech, I see growing real-world evidence backing up the insights of game theory.

The lessons are simple yet profound: Playing a game together to achieve mutual interests is better than playing exclusively with self-interest in mind.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Kate Vitasek, The Conversation

This knot has Gauss code O1U2O3U1O2U3. Credit: Graphic by Sam Nelson.

In the 19th century, Lord Kelvin made the inspired guess that elements are knots in the “ether”. Hydrogen would be one kind of knot, oxygen a different kind of knot—and so forth throughout the periodic table of elements. This idea led Peter Guthrie Tait to prepare meticulous and quite beautiful tables of knots, in an effort to elucidate when two knots are truly different. From the point of view of physics, Kelvin and Tait were on the wrong track: the atomic viewpoint soon made the theory of ether obsolete. But from the mathematical viewpoint, a gold mine had been discovered: The branch of mathematics now known as “knot theory” has been burgeoning ever since.

In his article “The Combinatorial Revolution in Knot Theory”, to appear in the December 2011 issue of the Notices of the AMS, Sam Nelson describes a novel approach to knot theory that has gained currency in the past several years and the mysterious new knot-like objects discovered in the process.

As sailors have long known, many different kinds of knots are possible; in fact, the variety is infinite. A *mathematical* knot can be imagined as a knotted circle: Think of a pretzel, which is a knotted circle of dough, or a rubber band, which is the “un-knot” because it is not knotted. Mathematicians study the patterns, symmetries, and asymmetries in knots and develop methods for distinguishing when two knots are truly different.

Mathematically, one thinks of the string out of which a knot is formed as being a one-dimensional object, and the knot itself lives in three-dimensional space. Drawings of knots, like the ones done by Tait, are projections of the knot onto a two-dimensional plane. In such drawings, it is customary to draw over-and-under crossings of the string as broken and unbroken lines. If three or more strands of the knot are on top of each other at single point, we can move the strands slightly without changing the knot so that every point on the plane sits below at most two strands of the knot. A planar knot diagram is a picture of a knot, drawn in a two-dimensional plane, in which every point of the diagram represents at most two points in the knot. Planar knot diagrams have long been used in mathematics as a way to represent and study knots.

As Nelson reports in his article, mathematicians have devised various ways to represent the information contained in knot diagrams. One example is the Gauss code, which is a sequence of letters and numbers wherein each crossing in the knot is assigned a number and the letter O or U, depending on whether the crossing goes over or under. The Gauss code for a simple knot might look like this: O1U2O3U1O2U3.

In the mid-1990s, mathematicians discovered something strange. There are Gauss codes for which it is impossible to draw planar knot diagrams but which nevertheless behave like knots in certain ways. In particular, those codes, which Nelson calls *nonplanar Gauss codes*, work perfectly well in certain formulas that are used to investigate properties of knots. Nelson writes: “A planar Gauss code always describes a [knot] in three-space; what kind of thing could a nonplanar Gauss code be describing?” As it turns out, there are “virtual knots” that have legitimate Gauss codes but do not correspond to knots in three-dimensional space. These virtual knots can be investigated by applying combinatorial techniques to knot diagrams.

Just as new horizons opened when people dared to consider what would happen if -1 had a square root—and thereby discovered complex numbers, which have since been thoroughly explored by mathematicians and have become ubiquitous in physics and engineering—mathematicians are finding that the equations they used to investigate regular knots give rise to a whole universe of “generalized knots” that have their own peculiar qualities. Although they seem esoteric at first, these generalized knots turn out to have interpretations as familiar objects in mathematics. “Moreover,” Nelson writes, “classical knot theory emerges as a special case of the new generalized knot theory.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to American Mathematical Society

You may have read the British Government is being petitioned to grant a posthumous pardon to one of the world’s greatest mathematicians and most successful codebreakers, Alan Turing. You may also have read that Turing was convicted of gross indecency in 1952 and died tragically two years later.

But who, exactly, was he?

Born in London in 1912, Turing helped lay the foundations of the “information age” we live in.

He did his first degree at King’s College, Cambridge, and then became a Fellow there. His first big contribution was his development of a mathematical model of computation in 1936. This became known as the Turing Machine.

It was not the first time a computer had been envisaged: that distinction belonged to Charles Babbage, a 19th century mathematician who designed a computer based on mechanical technology and built parts of it (some of which may be seen at the Science Museum in London or Powerhouse Museum in Sydney, for example).

But Babbage’s design was necessarily complicated, as he aimed for a working device using specific technology. Turing’s design was independent of any particular technology and was not intended to be built.

It was very simple and would be very inefficient and impractical as a device for doing real computations. But its simplicity meant it could be used to do mathematical reasoning about computation.

Turing used his abstract machines to investigate what kinds of things could be computed. He found some tasks which, although perfectly well defined and mathematically precise, are uncomputable. The first of these is known as the halting problem, which asks, for any given computation, whether it will ever stop. Turing showed that this was uncomputable: there is no systematic method that always gives the right answer.

So, if you have ever wanted a program that can run on your laptop and test all your other software to determine which of them might cause your laptop to “hang” or get stuck in a never-ending loop, the bad news is such a comprehensive testing program cannot be written.

Uncomputability is not confined to questions about the behaviour of computer programs. Since Turing’s work, many problems in mainstream mathematics have been found to be uncomputable. For example, the Russian mathematician and computer scientist, Yuri Matiyasevich, showed in 1970 that determining if a polynomial equation with several variables has a solution consisting only of whole numbers is also an uncomputable problem.

Turing machines have been used to define measures of the efficiency of computations. They underpin formal statements of the P vs NP problem, one of the Millennium Prize problems.

Another important feature of Turing’s model is its capacity to treat programs as data. This means the programs that tell computers what to do can themselves, after being represented in symbolic form, be given as input to other programs. Turing Machines that can take any program as input, and run that program on some input data, are called Universal Turing Machines.

These are really conceptual precursors of today’s computers, which are stored-program computers, in that they can treat programs as data in this sense. The oldest surviving intact computer in the world, in this most complete sense of the term, is CSIRAC at Melbourne Museum.

It seems a mathematical model of computation was an idea whose time had come. In 1936, the year of Turing’s result, another model of computation was published by Alonzo Church of Princeton University. Although Turing and Church took quite different routes, they ended up at the same place, in that the two models give exactly the same notion of computability.

In other words, the classification of tasks into computable and uncomputable is independent of which of these two models is used.

Other models of computation have been proposed, but mostly they seem to lead to the same view of what is and is not computable. The Church-Turing Thesis states that this class of computable functions does indeed capture exactly those things which can be computed in principle (say by a human with unlimited time, paper and ink, who works methodically and makes no mistakes).

It implies Turing Machines give a faithful mathematical model of computation. This is not a formal mathematical result, but rather a working assumption which is now widely accepted.

Turing went to Princeton and completed his PhD under Church, returning to Britain in 1938.

Early in the Second World War, Turing joined the British codebreaking operation at Bletchley Park, north-west of London. He became one of its most valuable assets. He was known by the nickname “Prof” and was described by colleague Jack Good as “a deep rather than a fast thinker”.

At the time, Germany was using an encryption device known as Enigma for much of its communications. This was widely regarded as completely secure. The British had already obtained an Enigma machine, from the Poles, and building on their work, Turing and colleague Gordon Welchman worked out how the Enigma-encrypted messages collected by the British could be decrypted.

Turing designed a machine called the Bombe, named after a Polish ice cream, which worked by testing large numbers of combinations of Enigma machine configurations, in order to help decrypt secret messages. These messages yielded information of incalculable value to the British. Winston Churchill described the Bletchley Park codebreakers as “geese that laid the golden eggs but never cackled”.

In 1945, after the war, Turing joined the National Physical Laboratory (NPL), where he wrote a report on how to construct an electronic computer, this time a general-purpose one unlike the machines dedicated to cryptanalysis which he helped to design at Bletchley Park.

This report led to the construction of an early computer (Pilot ACE) at NPL in 1950. By then, Turing had already moved on to Manchester University, where he worked on the first general-purpose stored-program computer in the world, the Manchester “Baby”.

In their early days, computers were often called “electronic brains”. Turing began to consider whether a computer could be programmed to simulate human intelligence, which remains a major research challenge today and helped to initiate the field of artificial intelligence.

A fundamental issue in such research is: how do you know if you have succeeded? What test can you apply to a program to determine if it has intelligence? Turing proposed that a program be deemed intelligent if, in its interaction with a human, the human is unable to detect whether he or she is communicating with another human or a computer program. (The test requires a controlled setting, for example where all communication with the human tester is by typed text.)

His paper on this topic – Computing Machinery and Intelligence – was published in 1950. The artificial intelligence community holds regular competitions to see how good researchers’ programs are at the Turing test.

The honours Turing received during his lifetime included an OBE in 1945 and becoming a Fellow of the Royal Society in 1951.

His wartime contributions remained secret throughout his life and for many years afterwards.

In 1952 he was arrested for homosexuality, which was illegal in Britain at the time. Turing was found guilty and required to undergo “treatment” with drugs. This conviction also meant he lost his security clearance.

In 1954 he ingested some cyanide, probably via an apple, and died. An inquest classified his death as suicide, and this is generally accepted today. But some at the time, including his mother, contended his death was an accidental consequence of poor handling of chemicals during some experiments he was conducting at home in his spare time.

The irony of Turing losing his security clearance – after the advantage his work had given Britain in the war, in extraordinary secrecy – is clear.

The magnitude of what was done to him has become increasingly plain over time, helped by greater availability of information about the work at Bletchley Park and changing social attitudes to homosexuality.

Next year, 2012, will be the centenary of Turing’s birth – with events planned globally to celebrate the man and his contribution. As this year approached, a movement developed to recognise Turing’s contribution and atone for what was done to him. In 2009, British Prime Minister, Gordon Brown, responding to a petition, issued a formal apology on behalf of the British government for the way Turing was treated.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Graham Farr, Monash University

Calculating probabilities can be complicated, as this classic “what’s behind the doors” problem shows, says Peter Rowlett.

Calculating probabilities can be tricky, with subtle changes in context giving quite different results. I was reminded of this recently after setting BrainTwister #10 for New Scientist readers, which was about the odds of seating two pairs of people adjacently in a row of 22 chairs.

Several readers wrote to say my solution was wrong. I had figured out all the possible seating arrangements and counted the ones that had the two groups adjacent. The readers, meanwhile, seated one pair first and then counted the ways of seating the second pair adjacently. Neither approach was wrong, depending on how you read the question.

This subtlety with probability is illustrated nicely by the Monty Hall problem, which is based on the long-running US game show Let’s Make a Deal. A contestant tries to guess which of three doors conceals a big prize. They guess at random, with ⅓ probability of finding the prize. In the puzzle, host Monty Hall doesn’t open the chosen door. Instead, he opens one of the other doors to reveal a “zonk”, an item of little value. He then offers the contestant the opportunity to switch to the remaining door or stick with their first choice.

Hall said in 1991 that the game is designed so contestants make the mistaken assumption that, since there are now two choices, their ⅓ probability has increased to ½. This, combined with a psychological preference to avoid giving up a prize already won, means people tend to stick

Marilyn vos Savant published the problem in her column in Parade magazine in 1990 along with the answer that you are much more likely to win if you switch. She received thousands of letters, many from mathematicians and scientists, telling her she was wrong.

Imagine the host opened one of the unchosen doors at random: one-third of the time, they would reveal the prize. But in the remaining cases, the prize would be behind the chosen door half the time, for a probability of ½.

But that isn’t really the problem being solved. The missing piece of information is that the host knows where the prize is, and of course the show must go on. There is a ⅓ probability that the prize is behind the chosen door, and therefore a ⅔ probability that it is behind one of the other two. Being shown a zonk behind one of the other two hasn’t changed this set-up – the door chosen still has a probability of ⅓, so the other door carries a ⅔ probability. You should switch.

Probability problems depend on the precise question more than people realise. This is why it might seem surprising when you run into a friend, because you aren’t considering the number of people you walked past and how many friends you might see. And for scientists, it is why they have to be very careful about what their evidence is really telling them.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Peter Rowlett*

Our laws of nature are written in the language of mathematics. But maths itself is only as dependable as the axioms it is built on, and we have to assume those axioms are true.

You might think that mathematics is the most trustworthy thing humans have ever come up with. It is the basis of scientific rigour and the bedrock of much of our other knowledge too. And you might be right. But be careful: maths isn’t all it seems. “The trustworthiness of mathematics is limited,” says Penelope Maddy, a philosopher of mathematics at the University of California, Irvine.

Maddy is no conspiracy theorist. All mathematicians know her statement to be true because their subject is built on “axioms” – and try as they might, they can never prove these axioms to be true.

An axiom is essentially an assumption based on observations of how things are. Scientists observe a phenomenon, formalise it and write down a law of nature. In a similar way, mathematicians use their observations to create an axiom. One example is the observation that there always seems to be a unique straight line that can be drawn between two points. Assume this to be universally true and you can build up the rules of Euclidean geometry. Another is that 1 + 2 is the same as 2 + 1, an assumption that allows us to do arithmetic. “The fact that maths is built on unprovable axioms is not that surprising,” says mathematician Vera Fischer at the University of Vienna in Austria.

These axioms might seem self-evident, but maths goes a lot further than arithmetic. Mathematicians aim to uncover things like the properties of numbers, the ways in which they are all related to one another and how they can be used to model the real world. These more complex tasks are still worked out through theorems and proofs built on axioms, but the relevant axioms might have to change. Lines between points have different properties on curved surfaces than flat ones, for example, which means the underlying axioms have to be different in different geometries. We always have to be careful that our axioms are reliable and reflect the world we are trying to model with our maths.

Set theory

The gold standard for mathematical reliability is set theory, which describes the properties of collections of things, including numbers themselves. Beginning in the early 1900s, mathematicians developed a set of underpinning axioms for set theory known as ZFC (for “Zermelo-Fraenkel”, from two of its initiators, Ernst Zermelo and Abraham Fraenkel, plus something called the “axiom of choice”).

ZFC is a powerful foundation. “If it could be guaranteed that ZFC is consistent, all uncertainty about mathematics could be dispelled,” says Maddy. But, brutally, that is impossible. “Alas, it soon became clear that the consistency of those axioms could be proved only by assuming even stronger axioms,” she says, “which obviously defeats the purpose.”

Maddy is untroubled by the limits: “Set theorists have been proving theorems from ZFC for 100 years with no hint of a contradiction.” It has been hugely productive, she says, allowing mathematicians to create no end of interesting results, and they have even been able to develop mathematically precise measures of just how much trust we can put in theories derived from ZFC.

In the end, then, mathematicians might be providing the bedrock on which much scientific knowledge is built, but they can’t offer cast-iron guarantees that it won’t ever shift or change. In general, they don’t worry about it: they shrug their shoulders and turn up to work like everybody else. “The aim of obtaining a perfect axiomatic system is exactly as feasible as the aim of obtaining a perfect understanding of our physical universe,” says Fischer.

At least mathematicians are fully aware of the futility of seeking perfection, thanks to the “incompleteness” theorems laid out by Kurt Gödel in the 1930s. These show that, in any domain of mathematics, a useful theory will generate statements about this domain that can’t be proved true or false. A limit to reliable knowledge is therefore inescapable. “This is a fact of life mathematicians have learned to live with,” says David Aspero at the University of East Anglia, UK.

All in all, maths is in pretty good shape despite this – and nobody is too bothered. “Go to any mathematics department and talk to anyone who’s not a logician, and they’ll say, ‘Oh, the axioms are just there’. That’s it. And that’s how it should be. It’s a very healthy approach,” says Fischer. In fact, the limits are in some ways what makes it fun, she says. “The possibility of development, of getting better, is exactly what makes mathematics an absolutely fascinating subject.”

HOW BIG IS INFINITY?

Infinity is infinitely big, right? Sadly, it isn’t that simple. We have long known that there are different sizes of infinity. In the 19th century, mathematician Georg Cantor showed that there are two types of infinity. The “natural numbers” (1, 2, 3 and so on forever) are a countable infinity. But between each natural number, there is a continuum of “real numbers” (such as 1.234567… with digits that go on forever). Real number infinities turn out not to be countable. And so, overall, Cantor concluded that there are two types of infinity, each of a different size.

In the everyday world, we never encounter anything infinite. We have to content ourselves with saying that the infinite “goes on forever” without truly grasping conceptually what that means. This matters, of course, because infinities crop up all the time in physics equations, most notably in those that describe the big bang and black holes. You might have expected mathematicians to have a better grasp of this concept, then – but it remains tricky.

This is especially true when you consider that Cantor suggested there might be another size of infinity nestled between the two he identified, an idea known as the continuum hypothesis. Traditionally, mathematicians thought that it would be impossible to decide whether this was true, but work on the foundations of mathematics has recently shown that there may be hope of finding out either way after all.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Michael Brooks*

Brian Hayes recently provided some evidence that there are still many out there who are confounded by the Monty Hall problem.

The Monty Hall problem, perhaps the best-known counter-intuitive probability problem, gets a nice treatment in Jeffery Rosenthal’s Struck by Lightning: The Curious World of Probabilities, and is also explained well (perhaps better) in Mark Haddon’s novel The Curious Incident of the Dog in the Night-time. Professor Rosenthal has some further Monty Hall explanations here.

I just found an alternate version of the problem in Martin Gardner’s The Second Scientific American Book of Mathematical Puzzles and Diversions (published also by Penguin in a slightly different form as More Mathematical Puzzles and Diversions). In the chapter “Probability and Ambiguity” (chapter 19 in both versions of the book), Gardner describes the problem of the three prisoners. Here is a condensed description of the problem:

Three prisoners, A, B, and C are in separate cells and sentenced to death. The governor has selected one of them at random to be pardoned. Finding out that one is to be released, prisoner A begs the warden to let him know the identity of one of the others who is going to be executed. “If B is to be pardoned, give me C’s name. If C is to be pardoned, give me B’s name. And if I’m to be pardoned, flip a coin to decide whether to name B or C.”

The warden tells A that B is to be executed. Prisoner A is pleased because he believes that his probability of surviving has gone up from 1/3 to 1/2. Prisoner A secretly tells C the news, who is also happy to hear it, believing that his chance of survival has also risen to 1/2.

Are A and C correct? No. Prisoner A’s probability of surviving is still 1/3, but prisoner C’s probability of receiving the pardon is 2/3.

It is reasonably easy to see that the 3 prisoners problem is the same as the Monty Hall problem. Seeing the problem in this different formulation might help those who continue to struggle with it.

It is a nice activity to simulate both the 3 prisoners problem and the Monty Hall problem in Fathom – try it and confirm the surprising results that the “second prisoner” is pardoned 2/3 of the time, and that 2/3 of the time, the winning curtain is not the one you selected first.

There are many, many, ways to write these simulations. Here are the attributes and formulas for a Fathom implementation of the three prisoners:

The table below (click on it to see a larger version) shows a separate simulation for the Monty Hall problem. Here we are assuming three curtains “1”, “2”, and “3”, one of which has a prize behind it. You pick one, and then Monty reveals the contents behind one of the other curtains (the curtain with the prize behind it is not shown). In the game, you have the option of switching your choice for the curtain that has not been revealed.

After creating the attributes, you can “run the simulation” by adding data to the collection (Collection->New Cases…), the more the better.

Incidentally, Gardner’s use of A, B, and C reminds me of Stephen Leacock’s “A, B, and C: The Human Element in Mathematics.”

Addendum

A quick search shows that the connection between the Monty Hall problem and the Three Prisoners is well known (see the wikipedia entries on Monty Hall and the Three Prisoners), and that both are alternate formulations of an older problem, known as Bertrand’s box paradox.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to dan.mackinnon*

Last year will go on record as one of significant natural disasters both in Australia and overseas. Indeed, the flooding of the Brisbane River in January is still making news as the Queensland floods inquiry investigates whether water released from Wivenhoe Dam was responsible. Water modelling is being used to answer the question: could modelling have avoided the problem in the first place?

This natural disaster – as well as the Japanese tsunami in March and the flooding in Bangkok in October – involved the movement of fluids: water, mud or both. And all had a human cost – displaced persons, the spread of disease, disrupted transport, disrupted businesses, broken infrastructure and damaged or destroyed homes. With the planet now housing 7 billion people, the potential for adverse humanitarian effects from natural disasters is greater than ever.

Here in CSIRO’s division of Mathematical and Information Sciences, we’ve been working with various government agencies (in Australia and China) to model the flow of flood waters and the debris they carry. Governments are starting to realise just how powerful computational modelling is for understanding and analysing natural disasters and how to plan for them.

This power is based on two things – the power of computers and the power of the algorithms (computer processing steps) that run on the computers.

In recent years, the huge increase in computer power and speed coupled with advances in algorithm development has allowed mathematical modellers like us to make large strides in our research.

These advances have enabled us to model millions, even billions of water particles, allowing us to more accurately predict the effects of natural and man-made fluid flows, such as tsunamis, dam breaks, floods, mudslides, coastal inundation and storm surges.

So how does it work?

Well, fluids such as sea water can be represented as billions of particles moving around, filling spaces, flowing downwards, interacting with objects and in turn being interacted upon. Or they can be visualised as a mesh of the fluids’ shape.

Let’s consider a tsunami such as the one that struck the Japanese coast in March of last year. When a tsunami first emerges as a result of an earthquake, shallow water modelling techniques give us the most accurate view of the wave’s formation and early movement.

Once the wave is closer to the coast however, techniques known collectively as smoothed particle hydrodynamics (SPH) are better at predicting how the wave interacts with local geography. We’ve created models of a hypothetical tsunami off the northern Californian coastline to test this.

A dam break can also be modelled using SPH. The modelling shows how fast the water moves at certain times and in certain places, where water “overtops” hills and how quickly it reaches towns or infrastructure such as power stations.

This can help town planners to build mitigating structures and emergency services to co-ordinate an efficient response. Our models have been validated using historical data from a real dam that broke in California in 1928 – the St. Francis Dam.

Having established that our modelling techniques work better than others, we can apply them to a range of what-if situations.

In collaboration with the Satellite Surveying and Mapping Application Centre in China we tested scenarios such as the hypothetical collapse of the massive Geheyan Dam in China.

We combined our modelling techniques with digital terrain models to get a realistic picture of how such a disaster would unfold and, therefore, what actions could mitigate it.

Our experience in developing and using these techniques over several decades allows us to combine them in unique ways for each situation.

We’ve modelled fluids not just for natural disaster planning but also movie special effects, hot metal production, water sports and even something as everyday as insurance.

Insurance companies have been looking to us for help to understand how natural disasters unfold. They cop a lot of media flak after disasters for not covering people affected. People living in low-lying areas have traditionally had difficulty accessing flood insurance and find themselves unprotected in flood situations.

Insurers are starting to realise that the modelling of geophysical flows can provide a basis for predicting localised risk of damage due to flooding and make flood coverage a viable business proposition. One Australian insurance company has been working with us to quantify risk of inundation in particular areas.

Using data from the 1974 Brisbane floods, the floods of last year and fluid modelling data, an insurance company can reliably assess residents’ exposure to particular risks and thereby determine suitable premiums.

With evidence-based tools such as fluid modelling in their arsenal, decision-makers are better prepared for the future. That may be a future of more frequent natural disasters, a future with a more-densely-populated planet, or, more likely, a combination of both.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Mahesh Prakash, CSIRO