Author: IMC

Around the world, political violence increased by 27% last year, affecting 1.7 billion people. The numbers come from the Armed Conflict Location & Event Data Project (ACLED), which collects real-time data on conflict events worldwide.

Some armed conflicts occur between states, such as Russia’s invasion of Ukraine. There are, however, many more that take place within the borders of a single state. In Nigeria, violence, particularly from Boko Haram, has escalated in the past few years. In Somalia, populations remain at risk amidst conflict and attacks perpetrated by armed groups, particularly Al-Shabaab.

To address the challenge of understanding how violent events spread, a team at the Complexity Science Hub (CSH) created a mathematical method that transforms raw data on armed conflicts into meaningful clusters by detecting causal links.

“Our main question was: what is a conflict? How can we define it?,” says CSH scientist Niraj Kushwaha, one of the co-authors of the study published in the latest issue of PNAS Nexus. “It was important for us to find a quantitative and bias-free way to see if there were any correlations between different violent events, just by looking at the data.”

“We often tell multiple narratives about a single conflict, which depend on whether we zoom in on it as an example of local tension or zoom out from it and consider it as part of a geopolitical plot; these are not necessarily incompatible,” explains co-author Eddie Lee, a postdoctoral fellow at CSH. “Our technique allows us to titrate between them and fill out a multiscale portrait of conflict.”

In order to investigate the many scales of political violence, the researchers turned to physics and biophysics for inspiration. The approach they developed is inspired by studies of stress propagation in collapsing materials and of neural cascades in the brain.

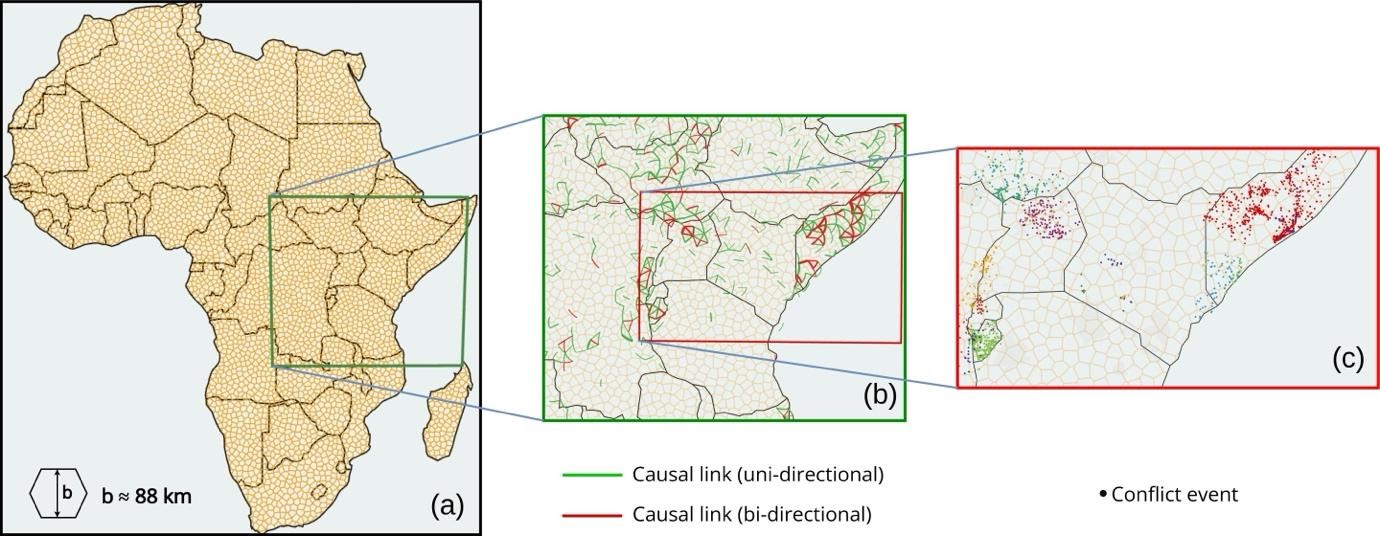
Kushwaha and Lee used data on violent battles in Africa between 1997 and 2019 from ACLED. In their analysis, they divided the geographic area into a grid of cells and time into sequential slices. The authors predicted when and where new battles would emerge by analysing the presence or absence of battles in each cell over time.

“If there’s a link between two cells, it means a conflict at one location can predict a conflict at another location,” explains Kushwaha. “By using this causal network, we can cluster different conflict events.”

Snow and sandpile avalanches

Observing the dynamics of the clusters, the scientists found that armed clashes spread like avalanches. “In a way evocative of snow or sandpile avalanches, a conflict originates in one place and cascades from there. There is a similar cascading effect in armed conflicts,” explains Kushwaha.

The team also identified a “mesoscale” for political violence —a time scale of a few days to months and a spatial scale of tens to hundreds of kilometers. Violence seems to propagate on these scales, according to Kushwaha and Lee.

Additionally, they found that their conflict statistics matched those from field studies such as in Eastern Nigeria, Somalia, and Sierra Leone. “We connected Fulani militia violence with Boko Haram battles in Nigeria, suggesting that these conflicts are related to one another,” details Kushwaha. The Fulani are an ethnic group living mainly in the Sahel and West Africa.

Policymakers and international agencies could benefit from the approach, according to the authors. The model could help uncover unseen causal links in violent conflicts. Additionally, it could one day help forecast the development of a war at an early stage. “By using this approach, policy decisions could be made more effectively, such as where resources should be allocated,” notes Kushwaha.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Complexity Science Hub Vienna

Number theory, the study of the properties of positive integers, is perhaps the purest form of mathematics. At first sight, it may seem far too abstract to apply to the natural world. In fact, the influential American number theorist Leonard Dickson wrote, “Thank God that number theory is unsullied by any application.”

And yet, again and again, number theory finds unexpected applications in science and engineering, from leaf angles that (almost) universally follow the Fibonacci sequence, to modern encryption techniques based on factoring prime numbers. Now, researchers have demonstrated an unexpected link between number theory and evolutionary genetics. Their work is published in the Journal of The Royal Society Interface.

Specifically, the team of researchers (from Oxford, Harvard, Cambridge, GUST, MIT, Imperial, and the Alan Turing Institute) have discovered a deep connection between the sums-of-digits function from number theory and a key quantity in genetics, the phenotype mutational robustness. This quality is defined as the average probability that a point mutation does not change a phenotype (a characteristic of an organism).

The discovery may have important implications for evolutionary genetics. Many genetic mutations are neutral, meaning that they can slowly accumulate over time without affecting the viability of the phenotype. These neutral mutations cause genome sequences to change at a steady rate over time. Because this rate is known, scientists can compare the percentage difference in the sequence between two organisms and infer when their latest common ancestor lived.

But the existence of these neutral mutations posed an important question: what fraction of mutations to a sequence are neutral? This property, called the phenotype mutational robustness, defines the average amount of mutations that can occur across all sequences without affecting the phenotype.

Professor Ard Louis from the University of Oxford, who led the study, said, “We have known for some time that many biological systems exhibit remarkably high phenotype robustness, without which evolution would not be possible. But we didn’t know what the absolute maximal robustness possible would be, or if there even was a maximum.”

It is precisely this question that the team has answered. They proved that the maximum robustness is proportional to the logarithm of the fraction of all possible sequences that map to a phenotype, with a correction which is given by the sums of digits function s_k(n), defined as the sum of the digits of a natural number n in base k. For example, for n = 123 in base 10, the digit sum would be s₁₀(123) = 1 + 2 + 3 = 6.

Another surprise was that the maximum robustness also turns out to be related to the famous Tagaki function, a bizarre function that is continuous everywhere, but differentiable nowhere. This fractal function is also called the blancmange curve, because it looks like the French dessert.

First author Dr. Vaibhav Mohanty (Harvard Medical School) added, “What is most surprising is that we found clear evidence in the mapping from sequences to RNA secondary structures that nature in some cases achieves the exact maximum robustness bound. It’s as if biology knows about the fractal sums-of-digits function.”

Professor Ard Louis added, “The beauty of number theory lies not only in the abstract relationships it uncovers between integers, but also in the deep mathematical structures it illuminates in our natural world. We believe that many intriguing new links between number theory and genetics will be found in the future.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to University of Oxford

Mathematicians at The University of Manchester have answered the question: How many lottery tickets do you need to buy to guarantee wining something on the U.K. National Lottery?

Focusing on the National Lottery’s flagship game “Lotto,” which draws six random numbersfrom 1 to 59, Dr. David Stewart and Dr. David Cushing found that 27 is the lowest possible number of tickets needed to guarantee a win—although, importantly, with no guarantee of a profit.

They describe the solution using a mathematical system called finite geometry, which centers around a triangle-like structure called a Fano plane. Each point of the structure is plotted with pairs of numbers and connected with lines—each line generates a set of six numbers, which equates to one ticket.

It takes three Fano planes and two triangles to cover all 59 numbers and generate 27 sets of tickets.

Choosing tickets in this way guarantees that no matter which of the 45,057,474 possible draws occurs, at least one of the tickets will have at least two numbers in common. From any draw of six, two numbers must appear on one of the five geometric structures, which ensures they appear on at least one ticket.

But Dr. Stewart and Dr. Cushing say that the hard work is actually showing that achieving the same outcome with 26 tickets is not possible.

Dr. David Stewart, a Reader in Pure Mathematics at The University of Manchester, said, “Fundamentally there is a tension which comes from the fact that there are only 156 entries on 26 tickets. This means a lot of numbers can’t appear a lot of times. Eventually you see that you’ll be able to find six numbers that don’t appear on any ticket together. In graph theory terms, we end up proving the existence of an independent set of size six.”

Although guaranteed a win, the researchers say that the chances of making a profit are very unlikely and shouldn’t be used as a reason to gamble.

The 27 lottery tickets would set you back £54. And Peter Rowlett, a mathematician from The Aperiodical website, has shown that in almost 99% of cases, you wouldn’t make that money back.

When putting the theory to the test in the lottery draw on 1 July 2023; the researchers matched just two balls on three of the tickets, the reward being three lucky dip tries on a subsequent lottery, each of which came to nothing.

The researchers say that the finding is interesting from a computational point of view. They use a fifty-year-old programming language called Prolog, which they say makes it one of the oldest examples of real artificial intelligence.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to University of Manchester

Buying a specific set of 27 tickets for the UK National Lottery will mathematically guarantee that you win something.

Buying 27 tickets ensures a win in the UK National Lottery

You can guarantee a win in every draw of the UK National Lottery by buying just 27 tickets, say a pair of mathematicians – but you won’t necessarily make a profit.

While there are many variations of lottery in the UK, players in the standard “Lotto” choose six numbers from 1 to 59, paying £2 per ticket. Six numbers are randomly drawn and prizes are awarded for tickets matching two or more.

David Cushing and David Stewart at the University of Manchester, UK, claim that despite there being 45,057,474 combinations of draws, it is possible to guarantee a win with just 27 specific tickets. They say this is the optimal number, as the same can’t be guaranteed with 26.

The proof of their idea relies on a mathematical field called finite geometry and involves placing each of the numbers from 1 to 59 in pairs or triplets on a point within one of five geometrical shapes, then using these to generate lottery tickets based on the lines within the shapes. The five shapes offer 27 such lines, meaning that 27 tickets bought using those numbers, at a cost of £54, will hit every possible winning combination of two numbers.

The 27 tickets that guarantee a win on the UK National Lottery

Their research yielded a specific list of 27 tickets (see above), but they say subsequent work has shown that there are two other combinations of 27 tickets that will also guarantee a win.

“We’ve been thinking about this problem for a few months. I can’t really explain the thought process behind it,” says Cushing. “I was on a train to Manchester and saw this [shape] and that’s the best logical [explanation] I can give.”

Looking at the winning numbers from the 21 June Lotto draw, the pair found their method would have won £1810. But the same numbers played on 1 July would have matched just two balls on three of the tickets – still a technical win, but giving a prize of just three “lucky dip” tries on a subsequent lottery, each of which came to nothing.

Stewart says proving that 27 tickets could guarantee a win was the easiest part of the research, while proving it is impossible to guarantee a win with 26 was far trickier. He estimates that the number of calculations needed to verify that would be 10¹⁶⁵, far more than the number of atoms in the universe. “There’d be absolutely no way to brute force this,” he says.

The solution was a computer programming language called Prolog, developed in France in 1971, which Stewart says is the “hero of the story”. Unlike traditional computer languages where a coder sets out precisely what a machine should do, step by step, Prolog instead takes a list of known facts surrounding a problem and works on its own to deduce whether or not a solution is possible. It takes these facts and builds on them or combines them in order to slowly understand the problem and whittle down the array of possible solutions.

“You end up with very, very elegant-looking programs,” says Stewart. “But they are quite temperamental.”

Cushing says the research shouldn’t be taken as a reason to gamble more, particularly as it doesn’t guarantee a profit, but hopes instead that it encourages other researchers to delve into using Prolog on thorny mathematical problems.

A spokesperson from Camelot, the company that operates the lottery, told New Scientist that the paper made for “interesting reading”.

“Our approach has always been to have lots of people playing a little, with players individually spending small amounts on our games,” they say. “It’s also important to bear in mind that, ultimately, Lotto is a lottery. Like all other National Lottery draw-based games, all of the winning Lotto numbers are chosen at random – any one number has the same and equal chance of being drawn as any other, and every line of numbers entered into a draw has the same and equal chance of winning as any other.”

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Matthew Sparkes*

In addition to describing biological interactions, evolutionary theory has also become a valuable tool to make sense of the dynamics of social norms. Social norms determine which behaviours should be regarded as positive, and how community members should act towards each other.

In a recent publication, published in PLOS Computational Biology, researchers from RIKEN, Japan, and the Max-Planck-Institute for Evolutionary Biology (MPI) describe a new class of social norms for cooperative interactions.

Social norms play an important role in people’s everyday lives. They govern how people should behave and how reputations are formed based on past behaviours.

In the last 25 years, there has been an effort to describe these dynamics of reputations more formally, using mathematical models borrowed from evolutionary game theory. These models describe how social norms evolve over time—how successful norms can spread in a society and how detrimental norms fade.

Most of these models assume that an individual’s reputation should only depend on what this person did in the past. However, everyday experience and experimental evidence suggest that additional external factors may as well influence a person’s reputation. People do not only earn a reputation for how they act, but also based on who they interact with, and how they are affected by those interactions.

For example, with a recent series of experiments, researchers from Harvard University have shown that victims of harmful actions are often regarded as more virtuous than they actually are. To explore such phenomena more formally, researchers at the MPI for Evolutionary Biology in Plön and RIKEN, Japan, have developed a new mathematical framework to describe social norms.

According to the new framework, when a person’s action affects the well-being of another community member, the reputations of both individuals may be updated. Using this general framework, the researchers explore which properties such norms ought have to support cooperative interactions. Surprisingly, some of these social norms indeed have the property observed in the earlier experiments: when one individual defects against another, the victim’s reputation should improve.

Moreover, the researchers also observe a fundamental trade-off. Norms that are particularly good in sustaining cooperation tend to be less robust with respect to noise (such as when reputations are shaped by third-party gossip).

Overall, this work is part of a bigger effort to understand key properties of social norms in a rigorous manner. These studies shed light on which ecological and social environments facilitate cooperation, and on the effects of social norms more generally.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Max Planck Society

In the face of existential dilemmas that are shared by all of humanity, including the consequences of inequality or climate change, it is crucial to understand the conditions leading to cooperation. A new game theory model developed at the Institute of Science and Technology Austria (ISTA) based on 192 stochastic games and on some elegant algebra finds that both cases—available information and the lack thereof—can lead to cooperative outcomes.

The journal Nature Communications has published a new open-access paper on the role information plays in reaching a cooperative outcome. Working at ISTA with the Chatterjee group, research scholar Maria Kleshnina developed a framework of stochastic games, a tool to describe how people make decisions in changing environments. The new model finds that availability of information is intricately linked to cooperative outcomes.

“In this paper, we present a new model of games where a group’s environment changes, based on actions of group members who do not necessarily have all relevant information about their environment. We find that there are rich interactions between the availability of information and cooperative behaviour.

“Counter-intuitively there are instances where there is a benefit of ignorance, and we characterize when information helps in cooperation,” says Professor Krishnendu Chatterjee who leads the “Computer-Aided Verification, Game Theory” group at the Institute of Science and Technology Austria, where this work was done.

Ignorance can be beneficial for cooperation too

In 2016, Štěpán Šimsa, one of the authors of the new paper was working with the Chatterjee group, when he ran some preliminary simulations to find that ignorance about the state of the game may benefit cooperation. This is counter-intuitive since the availability of information is generally thought to be universally beneficial. Christian Hilbe, then a postdoc with the Chatterjee group, along with Kleshnina, thought this to be a worthy research direction. The group then took on the task of investigating how information or the lack thereof affects the evolution of cooperation.

“We quantified in which games it is useful to have precise information about the environmental state. And we find that in most cases, around 80 to 90% it is indeed really good if players are aware of the environment’s state and which game they are playing right now. Yet, we also find some very interesting exceptional cases, where it’s actually optimal for cooperation if everyone is ignorant about the game they are playing,” says co-author Christian Hilbe, who now leads the research group Dynamics of Social Behaviour at the Max Planck Institute for Evolutionary Biology in Germany.

The researchers’ framework represents an idealized model for cooperation in changing environments. Therefore, the results cannot be directly transferred to real-world applications like solving climate change. For this, they say, a more extensive model would be required. Although, from the basic science model that she has built, Kleshnina is able to offer a qualitative direction.

“In a changing system, a benefit of ignorance is more likely to occur in systems that naturally punish non-cooperation. This could happen, for example, if the group’s environment quickly deteriorates if players no longer cooperate mutually. In such a system, individuals have strong incentives to cooperate today, if they want to avoid playing an unprofitable game tomorrow,” she says.

To illustrate the benefit of ignorance, Kleshnina says, “For example, we found that in informed populations, individuals can use their knowledge to employ more nuanced strategies. These nuanced strategies, however, can be less effective in sustaining cooperation. In such a case, there is indeed a small benefit of ignorance towards cooperation.”

A brilliant method

Game theory is, in its essence, a study of mathematical models set up within the framework of games or exchange of logical decisions being played between rational players. Its applications in understanding social and biological evolution have been welcomed by interdisciplinary researchers given its game-changing approach.

Within the context of evolutionary game theory, many models investigate cooperation but most assume that the same game is played over and over again, and also that the players are always perfectly aware of the game that they are playing and its state at any given moment. The new study weakens these general assumptions, first by allowing the simulated players to play different games over time. And second, by accounting for the impact of information.

“The beauty of this approach is that one can combine some elegant linear algebra with extensive computer simulations,” says Kleshnina.

The new framework opens up many new research directions. For instance, what is the role of asymmetric information? One player might know the exact game being played, but another may not. This is not something that the model currently covers. “In that sense, our paper has quite [a few] future applications within theory itself,” Hilbe adds.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Institute of Science and Technology Austria

Everyone knows that 2 + 2 = 4, but why do we have arithmetic in the first place, and why is it true? Researchers at the University of Canterbury have recently answered these questions by “reverse engineering” arithmetic from a psychological perspective. To do this, they considered all possible ways that quantities could be combined, and proved (for the first time in mathematical terms) that addition and multiplication are the simplest.

Their proof is based on four assumptions—principles of perceptual organization—that shape how we and other animals experience the world. These assumptions eliminate all possibilities except arithmetic, like how a sculptor’s work reveals a statue hidden in a block of stone.

Monotonicity is the idea of “things changing in the same direction,” and helps us keep track of our place in the world, so that when we approach an object it looms larger but smaller when we move away. Convexity is grounded in intuitions of betweenness. For example, the four corners of a football pitch define the playing field even without boundary lines connecting them. Continuity describes the smoothness with which objects seem to move in space and time. Isomorphism is the idea of sameness or analogy. It’s what allows us to recognize that a cat is more similar to a dog than it is to a rock.

Taken together, these four principles structure our perception of the world so that our everyday experience is ordered and cognitively manageable.

The implications, explained in a paper in Psychological Review, are far-reaching because arithmetic is fundamental for mathematics and science. They suggest arithmetic is biologically-based and a natural consequence of our perception. Mathematics is thus a realization in symbols of the fundamental nature of the mind, and as such both invented and discovered. The seemingly magical success of mathematics in the physical sciences hints that our mind and the world are not separate, but part of a common unity.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to University of Canterbury

You thought the maze looked fun, but now you can’t find your way out. Luckily, mathematics is here to help you escape, says Katie Steckles.

Getting lost in a maze is no fun, and on that rare occasion when you find yourself stuck in one without a map or a bird’s-eye view, it can be difficult to choose which way to go. Mathematics gives us a few tools we can use – in particular, topology, which concerns shapes and how they connect.

The most devious mazes are designed to be as confusing as possible, with dead ends and identical-looking junctions. But there is a stunningly simple rule that will always get you out of a maze, no matter how complicated: always turn right.

Any standard maze can be solved with this method (or its equivalent, the “always-turn-left” method). To do it, place one hand on the wall of the maze as you go in and keep it there. Each time you come to a junction, keep following the wall – if there is an opening on the side you are touching, take it; otherwise go straight. If you hit a dead end, turn around and carry on.

The reason this works is because the walls of any solvable maze will always have at least two distinct connected pieces: one to the left of the optimal solution path (shown in red), and one to the right. The section of wall next to the entrance is part of the same connected chunk of maze as the wall by the exit, and if you keep your hand on it, you will eventually walk along the whole length of the edge of this object – no matter how many twists and turns this involves – and reach the part at the exit.

While it is guaranteed to work, this certainly won’t be the most efficient path – you might find you traverse as much as half of the maze in the process, or even more depending on the layout. But at least it is easy to remember the rule.

Some mazes have more than two pieces. In these, disconnected sections of wall (shown in yellow) inside the maze create loops. In this case, if you start following the wall somewhere in the middle of the maze, there is a chance it could be part of an isolated section, which would leave you walking around a loop forever. But if you start from a wall that is connected to the outside, wall-following will still get you out.

It is reassuring to know that even if you are lost in a maze, you can always get out by following some variation on this rule: if you notice you have reached part of the maze you have been to before, you can detect loops, and switch to the opposite wall.

This is especially useful for mazes where the goal is to get to the centre: if the centre isn’t connected to the outside, wall-following won’t work, and you will need to switch walls to get onto the centre component. But as long as there are a finite number of pieces to the maze, and you keep trying different ones, you will eventually find a piece that is connected to your goal. You might, however, miss the bus home.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Katie Steckles*

Board games based on numbers, like Monopoly, Othello and Chutes and Ladders, make young children better at math, according to a comprehensive review of research published on the topic over the last 23 years.

Board games are already known to enhance learning and development including reading and literacy.

Now this new study, published in the journal Early Years, finds, for 3- to 9-year-olds, the format of number-based board games helps to improve counting, addition, and the ability to recognize if a number is higher or lower than another.

The researchers say children benefit from programs—or interventions—where they play board games a few times a week supervised by a teacher or another trained adult.

“Board games enhance mathematical abilities for young children,” says lead author Dr. Jaime Balladares, from Pontificia Universidad Católica de Chile, in Santiago, Chile.

“Using board games can be considered a strategy with potential effects on basic and complex math skills.

“Board games can easily be adapted to include learning objectives related to mathematical skills or other domains.”

Games where players take turns to move pieces around a board differ from those involving specific skills or gambling.

Board game rules are fixed which limits a player’s activities, and the moves on the board usually determine the overall playing situation.

However, preschools rarely use board games. This study aimed to compile the available evidence of their effects on children.

The researchers set out to investigate the scale of the effects of physical board games in promoting learning in young children.

They based their findings on a review of 19 studies published from 2000 onwards involving children aged from 3 to 9 years. All except one study focused on the relationship between board games and mathematical skills.

All children participating in the studies received special board game sessions which took place on average twice a week for 20 minutes over one-and-a-half months. Teachers, therapists, or parents were among the adults who led these sessions.

In some of the 19 studies, children were grouped into either the number board game or to a board game that did not focus on numeracy skills. In others, all children participated in number board games but were allocated different types (e.g., Dominoes).

All children were assessed on their math performance before and after the intervention sessions which were designed to encourage skills such as counting out loud.

The authors rated success according to four categories including basic numeric competency such as the ability to name numbers, and basic number comprehension (e.g., ‘nine is greater than three’).

The other categories were deepened number comprehension—where a child can accurately add and subtract—and interest in mathematics.

In some cases, parents attended a training session to learn arithmetic that they could then use in the games.

Results showed that math skills improved significantly after the sessions among children for more than half (52%) of the tasks analysed.

In nearly a third (32%) of cases, children in the intervention groups gained better results than those who did not take part in the board game intervention.

The results also show that from analysed studies to date, board games on the language or literacy areas, while implemented, did not include scientific evaluation (i.e. comparing control with intervention groups, or pre and post-intervention) to evaluate their impact on children.

Designing and implementing board games along with scientific procedures to evaluate their efficacy, therefore, are “urgent tasks to develop in the next few years,” Dr. Balladares, who was previously at UCL, argues.

And this, now, is the next project they are investigating.

Dr. Balladares concludes, “Future studies should be designed to explore the effects that these games could have on other cognitive and developmental skills.

“An interesting space for the development of intervention and assessment of board games should open up in the next few years, given the complexity of games and the need to design more and better games for educational purposes.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Taylor & Francis

Putting off college math could improve the likelihood that students remain in college. But that may only be true as long as students don’t procrastinate more than one year. This is what colleagues and I found in a study published in 2023 of 1,119 students at a public university for whom no remedial coursework was required during their first year.

Enrolling in a math course during the first semester of college resulted in students being four times more likely to drop out. Although delayed enrollment in a math course had benefits in the first year, its advantages vanished by the end of the second year. In our study, almost 40% of students who postponed the course beyond a year did not attempt it at all and failed to obtain a degree within six years.

Why it matters

Nearly 1.7 million students who recently graduated from high school will immediately enroll in college. Math is a requirement for most degrees, but students aren’t always ready to do college-level math. By putting off college math for a year, it gives students time to adjust to college and prepare for more challenging coursework.

Approximately 40% of four-year college students must first take a remedial math course. This can extend the time it takes to graduate and increase the likelihood of dropping out. Our study did not apply to students who need remedial math.

For students who do not require remedial courses, some delay can be beneficial, but students’ past experiences in math can lead to avoidance of math courses. Many students experience math anxiety. Procrastination can be an avoidance strategy for managing fears about math. The fear of math for students may be a more significant barrier than their performance.

It is estimated that at least 17% of the population will likely experience high levels of math anxiety. Math anxiety can lead to a drop in math performance. It can also lead to avoiding majors and career paths involving math.

Our study fills the void in research on the effects of how soon students take college-level math courses. It also supports prior evidence that students benefit from a mix of coursework that is challenging yet not overwhelming as they transition to college.

What still isn’t known

We believe colleges need to better promote student confidence in math by examining how student success courses can reduce math anxiety. Student success courses provide students with study skills, note-taking skills, goal setting, time management and stress management, as well as career and financial decision making to support the transition to college. Although student success courses are a proven practice that help students stick with college, rarely do these courses address students’ fear of math.

Students are at the greatest risk of dropping out of college during their first year. Advisors play a crucial role in providing students with resources for success. This includes recommendations on what courses to take and when to take them. More research is also needed about how advisors can effectively communicate the impact of when math is taken by students.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Forrest Lane, The Conversation