It is said that the ancient Greek philosopher Pythagoras came up with the idea that musical note combinations sound best in certain mathematical ratios, but that doesn’t seem to be true.
Pythagoras has influenced Western music for millennia
An ancient Greek belief about the most pleasing combinations of musical notes – often attributed to the philosopher Pythagoras – doesn’t actually reflect the way people around the world appreciate harmony, researchers have found. Instead, Pythagoras’s mathematical arguments may merely have been taken as fact and used to assert the superiority of Western culture.
According to legend, Pythagoras found that the ringing sounds of a blacksmith’s hammers sounded most pleasant, or “consonant”, when the ratio between the size of two tools involved two integers, or whole numbers, such as 3:2.
This idea has shaped how Western musicians play chords, because the philosopher’s belief that listeners prefer music played in perfect mathematical ratios was so influential. “Consonance is a really important concept in Western music, in particular for telling us how we build harmonies,” says Peter Harrison at the University of Cambridge.
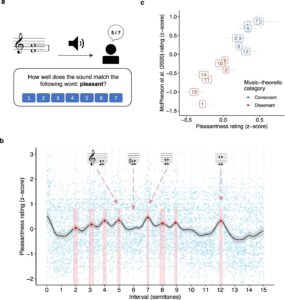
But when Harrison and his colleagues surveyed 4272 people in the UK and South Korea about their perceptions of music, their findings flew in the face of this ancient idea.
In one experiment, participants were played musical chords and asked to rate how pleasant they seemed. Listeners were found to slightly prefer sounds with an imperfect ratio. Another experiment discovered little difference in appeal between the sounds made by instruments from around the world, including the bonang, an Indonesian gong chime, which produces harmonies that cannot be replicated on a Western piano.
While instruments like the bonang have traditionally been called “inharmonic” by Western music culture, study participants appreciated the sounds the instrument and others like it made. “If you use non-Western instruments, you start preferring different harmonies,” says Harrison.
“It’s fascinating that music can be so universal yet so diverse at the same time,” says Patrick Savage at the University of Auckland, New Zealand. He says that the current study also contradicts previous research he did with some of the same authors, which found that integer ratio-based rhythms are surprisingly universal.
Michelle Phillips at the Royal Northern College of Music in Manchester, UK, points out that the dominance of Pythagorean tunings, as they are known, has been in question for some time. “Research has been hinting at this for 30 to 40 years, as music psychology has grown as a discipline,” she says. “Over the last fifteenish years, people have undertaken more work on music in the whole world, and we now know much more about non-Western pitch perception, which shows us even more clearly how complex perception of harmony is.”
Harrison says the findings tell us both that Pythagoras was wrong about music – and that music and music theory have been too focused on the belief that Western views are held worldwide. “The idea that simple integer ratios are superior could be framed as an example of mathematical justification for why we’ve got it right over here,” he says. “What our studies are showing is that, actually, this is not an inviolable law. It’s something that depends very much on the way in which you’re playing music.”
For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to Chris Stokel-Walker*