By rapidly analysing large amounts of data and making accurate predictions, artificial intelligence (AI) tools could help to answer many long-standing research questions. For instance, they could help to identify new materials to fabricate electronics or the patterns in brain activity associated with specific human behaviours.
One area in which AI has so far been rarely applied is number theory, a branch of mathematics focusing on the study of integers and arithmetic functions. Most research questions in this field are solved by human mathematicians, often years or decades after their initial introduction.
Researchers at the Israel Institute of Technology (Technion) recently set out to explore the possibility of tackling long-standing problems in number theory using state-of-the-art computational models.
In a recent paper, published in the Proceedings of the National Academy of Sciences, they demonstrated that such a computational approach can support the work of mathematicians, helping them to make new exciting discoveries.
“Computer algorithms are increasingly dominant in scientific research, a practice now broadly called ‘AI for Science,'” Rotem Elimelech and Ido Kaminer, authors of the paper, told Phys.org.
“However, in fields like number theory, advances are often attributed to creativity or human intuition. In these fields, questions can remain unresolved for hundreds of years, and while finding an answer can be as simple as discovering the correct formula, there is no clear path for doing so.”
Elimelech, Kaminer and their colleagues have been exploring the possibility that computer algorithms could automate or augment mathematical intuition. This inspired them to establish the Ramanujan Machine research group, a new collaborative effort aimed at developing algorithms to accelerate mathematical research.
Their research group for this study also included Ofir David, Carlos de la Cruz Mengual, Rotem Kalisch, Wolfram Berndt, Michael Shalyt, Mark Silberstein, and Yaron Hadad.
“On a philosophical level, our work explores the interplay between algorithms and mathematicians,” Elimelech and Kaminer explained. “Our new paper indeed shows that algorithms can provide the necessary data to inspire creative insights, leading to discoveries of new formulas and new connections between mathematical constants.”
The first objective of the recent study by Elimelech, Kaminer and their colleagues was to make new discoveries about mathematical constants. While working toward this goal, they also set out to test and promote alternative approaches for conducting research in pure mathematics.
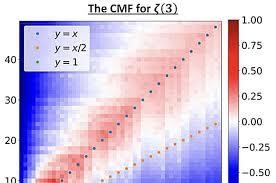
“The ‘conservative matrix field’ is a structure analogous to the conservative vector field that every math or physics student learns about in first year of undergrad,” Elimelech and Kaminer explained. “In a conservative vector field, such as the electric field created by a charged particle, we can calculate the change in potential using line integrals.
“Similarly, in conservative matrix fields, we define a potential over a discrete space and calculate it through matrix multiplications rather than using line integrals. Traveling between two points is equivalent to calculating the change in the potential and it involves a series of matrix multiplications.”
In contrast with the conservative vector field, the so-called conservative matrix field is a new discovery. An important advantage of this structure is that it can generalize the formulas of each mathematical constant, generating infinitely many new formulas of the same kind.
“The way by which the conservative matrix field creates a formula is by traveling between two points (or actually, traveling from one point all the way to infinity inside its discrete space),” Elimelech and Kaminer said. “Finding non-trivial matrix fields that are also conservative is challenging.”
As part of their study, Elimelech, Kaminer and their colleagues used large-scale distributed computing, which entails the use of multiple interconnected nodes working together to solve complex problems. This approach allowed them to discover new rational sequences that converge to fundamental constants (i.e., formulas for these constants).
“Each sequence represents a path hidden in the conservative matrix field,” Elimelech and Kaminer explained. “From the variety of such paths, we reverse-engineered the conservative matrix field. Our algorithms were distributed using BOINC, an infrastructure for volunteer computing. We are grateful to the contribution by hundreds of users worldwide who donated computation time over the past two and a half years, making this discovery possible.”
The recent work by the research team at the Technion demonstrates that mathematicians can benefit more broadly from the use of computational tools and algorithms to provide them with a “virtual lab.” Such labs provide an opportunity to try ideas experimentally in a computer, resembling the real experiments available in physics and in other fields of science. Specifically, algorithms can carry out mathematical experiments providing formulas that can be used to formulate new mathematical hypotheses.
“Such hypotheses, or conjectures, are what drives mathematical research forward,” Elimelech and Kaminer said. “The more examples supporting a hypothesis, the stronger it becomes, increasing the likelihood to be correct. Algorithms can also discover anomalies, pointing to phenomena that are the building-blocks for new hypotheses. Such discoveries would not be possible without large-scale mathematical experiments that use distributed computing.”
Another interesting aspect of this recent study is that it demonstrates the advantages of building communities to tackle problems. In fact, the researchers published their code online from their project’s early days and relied on contributions by a large network of volunteers.
“Our study shows that scientific research can be conducted without exclusive access to supercomputers, taking a substantial step toward the democratization of scientific research,” Elimelech and Kaminer said. “We regularly post unproven hypotheses generated by our algorithms, challenging other math enthusiasts to try proving these hypotheses, which when validated are posted on our project website. This happened on several occasions so far. One of the community contributors, Wolfgang Berndt, got so involved that he is now part of our core team and a co-author on the paper.”
The collaborative and open nature of this study allowed Elimelech, Kaminer and the rest of the team to establish new collaborations with other mathematicians worldwide. In addition, their work attracted the interest of some children and young people, showing them how algorithms and mathematics can be combined in fascinating ways.
In their next studies, the researchers plan to further develop the theory of conservative matrix fields. These matrix fields are a highly powerful tool for generating irrationality proofs for fundamental constants, which Elimelech, Kaminer and the team plan to continue experimenting with.
“Our current aim is to address questions regarding the irrationality of famous constants whose irrationality is unknown, sometimes remaining an open question for over a hundred years, like in the case of the Catalan constant,” Elimelech and Kaminer said.
“Another example is the Riemann zeta function, central in number theory, with its zeros at the heart of the Riemann hypothesis, which is perhaps the most important unsolved problem in pure mathematics. There are many open questions about the values of this function, including the irrationality of its values. Specifically, whether ζ(5) is irrational is an open question that attracts the efforts of great mathematicians.”
The ultimate goal of this team of researchers is to successfully use their experimental mathematics approach to prove the irrationality of one of these constants. In the future, they also hope to systematically apply their approach to a broader range of problems in mathematics and physics. Their physics-inspired hands-on research style arises from the interdisciplinary nature of the team, which combines people specialized in CS, EE, math, and physics.
“Our Ramanujan Machine group can help other researchers create search algorithms for their important problems and then use distributed computing to search over large spaces that cannot be attempted otherwise,” Elimelech and Kaminer added. “Each such algorithm, if successful, will help point to new phenomena and eventually new hypotheses in mathematics, helping to choose promising research directions. We are now considering pushing forward this strategy by setting up a virtual user facility for experimental mathematics,” inspired by the long history and impact of user facilities for experimental physics.
For more insights like this, visit our website at www.international-maths-challenge.com.
Credit of the article given to Ingrid Fadelli , Phys.org