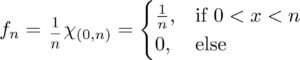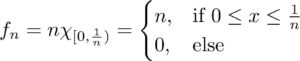Category: International Maths Olympiad

This post is the second example in an ongoing list of various sequences of functions which converge to different things in different ways.

‍Example 2

A sequence of functions {fn:R→R}{fn:R→R} which converges to 0 uniformly but does not converge to 0 in L1L1.

This works because:  The sequence tends to 0 as n→∞n→∞ since the height of each function tends to 0 and the the region where fnfn is taking on this decreasing height is tending towards all of R+R+ ((0,n)(0,n) as n→∞n→∞) (and it’s already 0 on R−∪{0}R−∪{0}). The convergence is uniform because the number of times we have to keep “squishing” the rectangles until their height is less than ϵϵ does not depend on xx.

The details: Let ϵ>0ϵ>0 and choose N∈NN∈N so that N>1ϵN>1ϵ and let n>Nn>N. Fix x∈Rx∈R.

Case 1 (x≤0x≤0 or x≥nx≥n) Then fn(x)=0fn(x)=0 and so |fn(x)−0|=0<ϵ|fn(x)−0|=0<ϵ.

• Case 2 (0<x<n0<x<n ) Then fn(x)=1nfn(x)=1n and so |fn(x)−0|=1n<1N<ϵ|fn(x)−0|=1n<1N<ϵ

Finally, fn↛0fn↛0 in L1L1 since∫R|fn|=∫(0,n)1n=1nλ((0,n))=1.∫R|fn|=∫(0,n)1n=1nλ((0,n))=1.

‍Remark: Here’s a question you could ask: wouldn’t fn=nχ(0,1n)fn=nχ(0,1n) work here too? Both are tending to 0 everywhere and both involve rectangles of area 1. The answer is “kinda.” The problem is that the convergence of nχ(0,1n)nχ(0,1n) is pointwise. BUT Egoroff’s Theorem gives us a way to actually “make” it uniform!.

‍On the notation above:   For a measurable set X⊂RX⊂R, denote the set of all Lebesgue integrable functions f:X→Rf:X→R by L1(X)L1(X). Then a sequence of functions {fn}{fn} is said to converge in L1L1  to a function ff if limn→∞∫|fn−f|=0limn→∞∫|fn−f|=0.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*

Given a sequence of real-valued functions {fn}{fn}, the phrase, “fnfn converges to a function ff” can mean a few things:

• fnfn converges uniformly
• fnfn converges pointwise
• fnfn converges almost everywhere (a.e.)
• fnfn converges in L1L1 (set of Lebesgue integrable functions)
• and so on…

Other factors come into play if the fnfn are required to be continuous, defined on a compact set, integrable, etc.. So since I do not have the memory of an elephant (whatever that phrase means…), I’ve decided to keep a list of different sequences that converge (or don’t converge) to different functions in different ways. With each example I’ll also include a little (and hopefully) intuitive explanation for why. Having these sequences close at hand is  especially useful when analysing the behavior of certain functions or constructing counterexamples.

The first sequence we’ll look at is one which converges almost everywhere, but does not converge in L1L1 (the set of Lebesgue integrable functions).

‍Example 1

A sequence of functions {fn:R→R}{fn:R→R} which converges to 0 almost everywhere but does not converge to 0 in L1L1.       

This works because: Recall that to say fn→0fn→0 almost everywhere means fn→0fn→0 pointwise on RR except for a set of measure 0. Here, the set of measure zero is the singleton set {0}{0} (at x=0x=0, fn(x)=nfn(x)=n and we can’t make this less than ϵϵ for any ϵ>0ϵ>0). So fnfn converges to 0 pointwise on (0,1](0,1]. This holds because if x<0x<0 or x>1x>1 then fn(x)=0fn(x)=0 for all nn. Otherwise, if x∈(0,1]x∈(0,1], we can choose nn appropriately:

The details:  Let ϵ>0ϵ>0 and x∈(0,1]x∈(0,1] and choose N∈NN∈N so that N>1xN>1x. Then whenever n>Nn>N, we have n>1xn>1x which implies x>1nx>1n and so fn(x)=0fn(x)=0. Hence |fnx−0|=0<ϵ|fnx−0|=0<ϵ.

Further*, fn↛0fn↛0 in L1L1 since∫R|fn|=∫[0,1n]n=nλ([0,1n])=1.∫R|fn|=∫[0,1n]n=nλ([0,1n])=1.

Remark: Notice that Egoroff’s theorem applies here! We just proved that fn→0fn→0 pointwise a.e. on RR, but Egoroff says that we can actually get uniform convergence a.e. on a bounded subset of RR, say (0,1](0,1].

In particular for each ϵ>0ϵ>0 we are guaranteed the existence of a subset E⊂(0,1]E⊂(0,1] such that fn→0fn→0 uniformly and λ((0,1]∖E)<ϵλ((0,1]∖E)<ϵ. In fact, it should be clear that that subset must be something like (ϵ2,1](ϵ2,1] (the “zero region” in the graph above). Then no matter where xx is in (0,1](0,1], we can always find nn large enough – namely all nn which satisfy 1n<ϵ21n<ϵ2 – so that fn(x)=0fn(x)=0, i.e. fn→ffn→f uniformly. And indeed, λ((0,1]∖(ϵ2,1]=ϵ/2<ϵλ((0,1]∖(ϵ2,1]=ϵ/2<ϵ as claimed.

‍On the notation above:   For a measurable set X⊂RX⊂R, denote the set of all Lebesgue integrable functions f:X→Rf:X→R by L1(X)L1(X). Then a sequence of functions {fn}{fn} is said to converge in L1L1  to a function ff if limn→∞∫|fn−f|=0limn→∞∫|fn−f|=0.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*

Using the tools of computational complexity, researchers have discovered it is impossible to figure out whether certain Super Mario Bros levels can be beaten without playing them, even if you use the world’s most powerful supercomputer.

Figuring out whether certain levels in the Super Mario Bros series of video games can be completed before you play them is mathematically impossible, even if you had several years and the world’s most powerful supercomputer to hand, researchers have found.

“We don’t know how to prove that a game is fun, we don’t know what that means mathematically, but we can prove that it’s hard and that maybe gives some insight into why it’s fun,” says Erik Demaine at the Massachusetts Institute of Technology. “I like to think of hard as a proxy for fun.”

To prove this, Demaine and his colleagues use tools from the field of computational complexity – the study of how difficult and time-consuming various problems are to solve algorithmically. They have previously proven that figuring out whether it is possible to complete certain levels in Mario games is a task that belongs to a group of problems known as NP-hard, where the complexity grows exponentially. This category is extremely difficult to compute for all but the smallest problems.

Now, Demaine and his team have gone one step further by showing that, for certain levels in Super Mario games, answering this question is not only hard, but impossible. This is the case for several titles in the series, including New Super Mario Bros and Super Mario Maker. “You can’t get any harder than this,” he says. “Can you get to the finish? There is no algorithm that can answer that question in a finite amount of time.”

While it may seem counterintuitive, problems in this undecidable category, known as RE-complete, simply cannot be solved by a computer, no matter how powerful, no matter how long you let it work.

Demaine concedes that a small amount of trickery was needed to make Mario levels fit this category. Firstly, the research looks at custom-made levels that allowed the team to place hundreds or thousands of enemies on a single spot. To do this they had to remove the limits placed by the game publishers on the number of enemies that can be present in a level.

They were then able to use the placement of enemies within the level to create an abstract mathematical tool called a counter machine, essentially creating a functional computer within the game.

That trick allowed the team to invoke another conundrum known as the halting problem, which says that, in general, there is no way to determine if a given computer program will ever terminate, or simply run forever, other than running it and seeing what happens.

These layers of mathematical concepts finally allowed the team to prove that no analysis of the game level can say for sure whether or not it can ever be completed. “The idea is that you’ll be able to solve this Mario level only if this particular computation will terminate, and we know that there’s no way to determine that, and so there’s no way to determine whether you can solve the level,” says Demaine.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Matthew Sparkes*

Our laws of nature are written in the language of mathematics. But maths itself is only as dependable as the axioms it is built on, and we have to assume those axioms are true.

You might think that mathematics is the most trustworthy thing humans have ever come up with. It is the basis of scientific rigour and the bedrock of much of our other knowledge too. And you might be right. But be careful: maths isn’t all it seems. “The trustworthiness of mathematics is limited,” says Penelope Maddy, a philosopher of mathematics at the University of California, Irvine.

Maddy is no conspiracy theorist. All mathematicians know her statement to be true because their subject is built on “axioms” – and try as they might, they can never prove these axioms to be true.

An axiom is essentially an assumption based on observations of how things are. Scientists observe a phenomenon, formalise it and write down a law of nature. In a similar way, mathematicians use their observations to create an axiom. One example is the observation that there always seems to be a unique straight line that can be drawn between two points. Assume this to be universally true and you can build up the rules of Euclidean geometry. Another is that 1 + 2 is the same as 2 + 1, an assumption that allows us to do arithmetic. “The fact that maths is built on unprovable axioms is not that surprising,” says mathematician Vera Fischer at the University of Vienna in Austria.

These axioms might seem self-evident, but maths goes a lot further than arithmetic. Mathematicians aim to uncover things like the properties of numbers, the ways in which they are all related to one another and how they can be used to model the real world. These more complex tasks are still worked out through theorems and proofs built on axioms, but the relevant axioms might have to change. Lines between points have different properties on curved surfaces than flat ones, for example, which means the underlying axioms have to be different in different geometries. We always have to be careful that our axioms are reliable and reflect the world we are trying to model with our maths.

Set theory

The gold standard for mathematical reliability is set theory, which describes the properties of collections of things, including numbers themselves. Beginning in the early 1900s, mathematicians developed a set of underpinning axioms for set theory known as ZFC (for “Zermelo-Fraenkel”, from two of its initiators, Ernst Zermelo and Abraham Fraenkel, plus something called the “axiom of choice”).

ZFC is a powerful foundation. “If it could be guaranteed that ZFC is consistent, all uncertainty about mathematics could be dispelled,” says Maddy. But, brutally, that is impossible. “Alas, it soon became clear that the consistency of those axioms could be proved only by assuming even stronger axioms,” she says, “which obviously defeats the purpose.”

Maddy is untroubled by the limits: “Set theorists have been proving theorems from ZFC for 100 years with no hint of a contradiction.” It has been hugely productive, she says, allowing mathematicians to create no end of interesting results, and they have even been able to develop mathematically precise measures of just how much trust we can put in theories derived from ZFC.

In the end, then, mathematicians might be providing the bedrock on which much scientific knowledge is built, but they can’t offer cast-iron guarantees that it won’t ever shift or change. In general, they don’t worry about it: they shrug their shoulders and turn up to work like everybody else. “The aim of obtaining a perfect axiomatic system is exactly as feasible as the aim of obtaining a perfect understanding of our physical universe,” says Fischer.

At least mathematicians are fully aware of the futility of seeking perfection, thanks to the “incompleteness” theorems laid out by Kurt Gödel in the 1930s. These show that, in any domain of mathematics, a useful theory will generate statements about this domain that can’t be proved true or false. A limit to reliable knowledge is therefore inescapable. “This is a fact of life mathematicians have learned to live with,” says David Aspero at the University of East Anglia, UK.

All in all, maths is in pretty good shape despite this – and nobody is too bothered. “Go to any mathematics department and talk to anyone who’s not a logician, and they’ll say, ‘Oh, the axioms are just there’. That’s it. And that’s how it should be. It’s a very healthy approach,” says Fischer. In fact, the limits are in some ways what makes it fun, she says. “The possibility of development, of getting better, is exactly what makes mathematics an absolutely fascinating subject.”

HOW BIG IS INFINITY?

Infinity is infinitely big, right? Sadly, it isn’t that simple. We have long known that there are different sizes of infinity. In the 19th century, mathematician Georg Cantor showed that there are two types of infinity. The “natural numbers” (1, 2, 3 and so on forever) are a countable infinity. But between each natural number, there is a continuum of “real numbers” (such as 1.234567… with digits that go on forever). Real number infinities turn out not to be countable. And so, overall, Cantor concluded that there are two types of infinity, each of a different size.

In the everyday world, we never encounter anything infinite. We have to content ourselves with saying that the infinite “goes on forever” without truly grasping conceptually what that means. This matters, of course, because infinities crop up all the time in physics equations, most notably in those that describe the big bang and black holes. You might have expected mathematicians to have a better grasp of this concept, then – but it remains tricky.

This is especially true when you consider that Cantor suggested there might be another size of infinity nestled between the two he identified, an idea known as the continuum hypothesis. Traditionally, mathematicians thought that it would be impossible to decide whether this was true, but work on the foundations of mathematics has recently shown that there may be hope of finding out either way after all.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Michael Brooks*

Yesterday I received a disheartening 44/50 on a homework assignment. Okay okay, I know. 88% isn’t bad, but I had turned in my solutions with so much confidence that admittedly, my heart dropped a little (okay, a lot!) when I received the grade. But I quickly had to remind myself, Hey! Grades don’t matter.

The six points were deducted from two problems. (Okay, fine. It was three. But in the third I simply made an air-brained mistake.) In the first, apparently my answer wasn’t explicit enough. How stingy! I thought. Doesn’t our professor know that this is a standard example from the book? I could solve it in my sleep! But after the prof went over his solution in class, I realized that in all my smugness I never actually understood the nuances of the problem. Oops. You bet I’ll be reviewing his solution again. Lesson learned.

In the second, I had written down my solution in the days before and had checked with a classmate and (yes) the internet to see if I was correct. Unfortunately, the odds were against me two-to-one as both sources agreed with each other but not with me. But I just couldn’t see how I could possibly be wrong! Confident that my errors were truths, I submitted my solution anyway, hoping there would be no consequences. But alas, points were taken off.

Honestly though, is a lower grade such a bad thing? I think not. In both cases, I learned exactly where my understanding of the material went awry. And that’s great! It means that my comprehension of the math is clearer now than it was before (and that the chances of passing my third qualifying exam have just increased. Woo!) And that’s precisely why I’m (still, heh…) in school.

So yes, contrary to what the comic above says, grades do exist in grad school, but – and this is what I think the comic is hinting at – they don’t matter. Your thesis committee members aren’t going to say, “Look, your defense was great, but we can’t grant you your PhD. Remember that one homework/midterm/final grade from three years ago?” (They may not use the word “great” either, but that’s another matter.) Of course, we students should still work hard and put in maximum effort! But the emphasis should not be on how well we perform, but rather how much we learn. Focus on the latter and the former will take care of itself. This is true in both graduate school and college, but the lack of emphasis on grades in grad school really brings it home. And personally, I’m very grateful for it because my brain is freed up to focus on other things like, I don’t know, learning math!

So to all my future imperfect homework scores out there: bring it on.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*