Category: Uncategorized

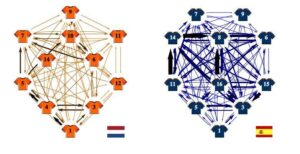
Passing networks for the Netherlands and Spain drawn before the final game, using the passing data and tactical formations of the semi-finals. Image from arXiv:1206.6904v1

For years, sports fanatics have turned to statistics to help them gauge the relative strength or weaknesses of different teams, though some have been more amenable to the process than others. Baseball and football, for example, seem to have a statistic for every action that occurs on the field of play, with different players ranked and rated by their numbers. International football, aka soccer on the other hand has generally defied such attempts due to their being far fewer things to measure with the sport and the continuity of play. That may change however, as mathematicians Javier López Peña and Hugo Touchette of University College and Queen Mary University respectively, have applied network theory to the unique style of play of the European Championship 2012 victor, Spain. And as they describe in the paper they’ve uploaded to the preprint server arXiv, the graphic that results gives some clues as to why the team is considered one of the best of all time.

Anyone who has watched the Spanish team knows that their style of play is different from other teams. So much so it’s been given a name by fans: tiki-taka. It’s all about quick passes and exquisite teamwork. But trying to describe what the team does only leads to superlatives, which don’t really get to the heart of the matter. To help, Peña and Touchette turned to network theory, which makes sense, because soccer is played as a network of teammates working efficiently together.

Unfortunately, on paper, network theory tends to wind up looking like a bunch of hard to decipher equations, which wouldn’t help anyone except those that create them. To make it so that anyone could understand what their theories have turned up, the two used a simple drawing depicting players as nodes and their relationship to one another on the team, the amount of passing that is done between them, the way it is done and to whom, as lines between the nodes.

What shows up in the drawing first, is what everyone already knows, namely, that the team passes the ball among its players a lot. More than a lot actually. In one match during 2010’s World Cup between Spain and the Netherlands, the Spanish players out-passed their opponent 417 to 266. The drawing also highlights the fact that two players on the team are “well connected” i.e. easy for others to get to, versus just one for the opponent.

The graphic also shows what is known as “betweenness centrality,” which is a way of measuring the amount a network relies on a single node to operate at its optimum capacity. With soccer, it measures how much a team relies on an individual player. In this instance, the opponent appears far more vulnerable to disruption if that individual is covered adequately than happens with the Spanish team. Also implemented in the graphic is the notion of PageRank, developed by Google, which ranks the most popular pages by linkages. Applied to soccer it would mean the player who is passed the ball most often by teammates. With Spain, of course, it was central midfielder, Xavi.

In many ways the graphic confirms what most suspect, that Spain wins more because it relies more on precise teamwork rather than the special skills of one or two superstars. In other ways though, it shows that even soccer can be made to offer up statistics if someone looks hard enough.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Bob Yirka , Phys.org

This shows a stretch of the M30. In the bottom left-hand corner, you can see the square frames under which the detectors are placed.

Technicians from Madrid City Council and a team of Pole and Spanish researchers have analysed the density and intensity of traffic on Madrid’s M30 motorway (Spain) throughout the day. By applying mathematical algorithms, they have verified that drivers should pay more attention to the road between 6pm and 8pm to avoid accidents.

Detection devices installed by the Department of Traffic Technologies of Madrid City Council on the M30 motorway and its access roads were used to conduct a scientific study. Researchers from SICE, the traffic management company in charge of this thoroughfare, used past records to develop a new device that determines the time during which more attention should be paid to the road.

This period is the same as the shortest lifetime of spatio-temporal correlations of traffic intensity. In the case of the M30, it has proven to be between 6pm and 8pm, according to the study published in the Central European Journal of Physics.

“Between 6pm and 8pm, the most ‘stop and go’ phenomena occur. In other words, some vehicles break and others set off or accelerate at different speeds,” as explained to SINC by Cristina Beltrán, SICE engineer, who goes on to say that “vehicle speeds at consecutive stretches of the motorway are less correlated during these periods.”

The researcher clarifies that traffic conditions that vary quickly in space and time means that “drivers should always pay more attention on the roads as to whether they should reduce or increase their speed or be aware of road sign recommendations.”

Reference data were taken during a ‘typical week’ on the 13 kilometre stretch of the M30 using detectors at intervals of approximately 500 metres. These devices record the passing speed of vehicles and also how busy the road is (the time that vehicles remain stationary in a given place). Then, using algorithms and models developed by AGH University of Science and Technology (Poland), correlations were analysed.

Free flow, Passing and Congested Traffic

The team focused mainly on the intensity of traffic (vehicles/hour) and density (vehicle/km) during the three phases of traffic: free flow, congested and an intermission named ‘passing’ or synchronised. The easiest to categorise is the first, where intensity and density grow exponentially with hardly any variation, but the other two also show correlations.

This information helps us to take traffic control measures during rush hours, provide speed recommendations that can alter traffic characteristics and offer alternative routes via less congested areas,” outlines Beltrán. “This is all part of Madrid City Council’s objective to actively research new systems for improving traffic flow on the M30.”

The study enjoyed the support of the European Union’s 7th Framework Programme through the SOCIONICAL Project (www.socionical.eu) and the results were cross-referenced with data from the USA’s Insurance Institute for Highway Safety. The work of this scientific and educational organisation is geared towards reducing human and material loss as a result of road accidents.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Spanish Foundation for Science and Technology (FECYT)

A side-by-side comparison of a standard flat driver’s side mirror with the mirror designed by Dr. R. Andrew Hicks, mathematics professor at Drexel University. With minimal distortion, Hicks’s mirror shows a much wider field of view (the wide area to the left of the silver car seen in the distance, behind the tree, in this image). Hicks’s mirror has a field of view of about 45 degrees, compared to 15 to 17 degrees of view in a flat mirror. Hicks’s mirror received a US patent in May 2012.

A side mirror that eliminates the dangerous “blind spot” for drivers has now received a U.S. patent. The subtly curved mirror, invented by Drexel University mathematics professor Dr. R. Andrew Hicks, dramatically increases the field of view with minimal distortion.

Traditional flat mirrors on the driver’s side of a vehicle give drivers an accurate sense of the distance of cars behind them but have a very narrow field of view. As a result, there is a region of space behind the car, known as the blind spot, that drivers can’t see via either the side or rear-view mirror. It’s not hard to make a curved mirror that gives a wider field of view; no blind spot; but at the cost of visual distortion and making objects appear smaller and farther away.

Hicks’s driver’s side mirror has a field of view of about 45 degrees, compared to 15 to 17 degrees of view in a flat driver’s side mirror. Unlike in simple curved mirrors that can squash the perceived shape of objects and make straight lines appear curved, in Hicks’s mirror the visual distortions of shapes and straight lines are barely detectable.

Hicks, a professor in Drexel’s College of Arts and Sciences, designed his mirror using a mathematical algorithm that precisely controls the angle of light bouncing off of the curving mirror.

“Imagine that the mirror’s surface is made of many smaller mirrors turned to different angles, like a disco ball,” Hicks said. “The algorithm is a set of calculations to manipulate the direction of each face of the metaphorical disco ball so that each ray of light bouncing off the mirror shows the driver a wide, but not-too-distorted, picture of the scene behind him.”

Hicks noted that, in reality, the mirror does not look like a disco ball up close. There are tens of thousands of such calculations to produce a mirror that has a smooth, nonuniform curve.

Hicks first described the method used to develop this mirror in Optics Letters in 2008

In the United States, regulations dictate that cars coming off of the assembly line must have a flat mirror on the driver’s side. Curved mirrors are allowed for cars’ passenger-side mirrors only if they include the phrase “Objects in mirror are closer than they appear.”

Because of these regulations, Hicks’s mirrors will not be installed on new cars sold in the U.S. any time soon. The mirror may be manufactured and sold as an aftermarket product that drivers and mechanics can install on cars after purchase. Some countries in Europe and Asia do allow slightly curved mirrors on new cars. Hicks has received interest from investors and manufacturers who may pursue opportunities to license and produce the mirror.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Drexel University

EU researchers contributed important knowledge to the field of modular representation theory in the form of proofs and pioneering analyses.

Modular representation theory studies linear actions on finite groups, or groups of a countable (finite) number of elements.

A discussion of finite groups requires definition of several associated terms. The so-called representation of a given finite group can be reduced using a prime integer to get a modular representation of the group (sort of breaking down the whole into the sum of its parts).

Mathematically, an indecomposable or irreducible module of a finite group has only two submodules, the module itself and zero. Vertices and sources are mathematical entities associated with indecomposable modules.

While modular representation theory has evolved tremendously, many issues still remain to be addressed. In particular, modules of symmetric groups, a type of finite group whose elements allow only a certain number of structure-preserving transformations, are an active area of interest.

European researchers supported by funding of the ‘Vertices of simple modules for the symmetric and related finite groups’ (D07.SYMGPS.OX) project sought to develop fast algorithms for computation of vertices and sources of indecomposable modules as well as to study the Auslander-Reiten quiver considered to be part of a presentation of the category of all representations.

Investigators first analysed two-modular Specht modules and the position of Specht modules in the Auslander-Reiten quiver with important definitive results.

In addition, the team produced ground-breaking proofs regarding the Lie module of the symmetric group, shedding light on a topic of mathematics until now clouded in mystery.

Furthermore, the Fiet conjecture was proved and innovative results were obtained regarding vertices of simple modules of symmetric groups.

Overall, the project team provided pioneering work and definitive results and proofs regarding symmetric groups and related finite groups that promise to significantly advance the mathematical field of modular representation theory.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to CORDIS

This graphic shows a matter wave hitting a Schrodinger’s hat. The wave inside the container is magnified. Outside, the waves wrap as if they had never encountered any obstacle. Credit: G. Uhlmann, U. of Washington

Invisibility, once the subject of magic or legend, is slowly becoming reality. Over the past five years mathematicians and other scientists have been working on devices that enable invisibility cloaks – perhaps not yet concealing Harry Potter, but at least shielding small objects from detection by microwaves or sound waves.

A University of Washington mathematician is part of an international team working to understand invisibility and extend its possible applications. The group has now devised an amplifier that can boost light, sound or other waves while hiding them inside an invisible container.

“You can isolate and magnify what you want to see, and make the rest invisible,” said corresponding author Gunther Uhlmann, a UW mathematics professor. “You can amplify the waves tremendously. And although the wave has been magnified a lot, you still cannot see what is happening inside the container.”

The findings were published this week in the Proceedings of the National Academy of Sciences.

As a first application, the researchers propose manipulating matter waves, which are the mathematical description of particles in quantum mechanics. The researchers envision building a quantum microscope that could capture quantum waves, the waves of the nanoworld. A quantum microscope could, for example, be used to monitor electronic processes on computer chips.

The authors dubbed their system “Schrödinger’s hat,” referring to the famed Schrödinger’s cat in quantum mechanics. The name is also a nod to the ability to create something from what appears to be nothing.

“In some sense you are doing something magical, because it looks like a particle is being created. It’s like pulling something out of your hat,” Uhlmann said.

Matter waves inside the hat can also be shrunk, though Uhlmann notes that concealing very small objects “is not so interesting.”

Uhlmann, who is on leave at the University of California, Irvine, has been working on invisibility with fellow mathematicians Allan Greenleaf at the University of Rochester, Yaroslav Kurylev at University College London in the U.K., and Matti Lassas at the University of Helsinki in Finland, all of whom are co-authors on the new paper.

The team helped develop the original mathematics to formulate cloaks, which must be realized using a class of engineered materials, dubbed metamaterials, that bend waves so that it appears as if there was no object in their path. The international team in 2007 devised wormholes in which waves disappear in one place and pop up somewhere else.

For this paper, they teamed up with co-author Ulf Leonhardt, a physicist at the University of St. Andrews in Scotland and author on one of the first papers on invisibility.

Recent progress suggests that a Schrodinger’s hat could, in fact, be built for some types of waves.

“From the experimental point of view, I think the most exciting thing is how easy it seems to be to build materials for acoustic cloaking,” Uhlmann said. Wavelengths for microwave, sound and quantum matter waves are longer than light or electromagnetic waves, making it easier to build the materials to cloak objects from observation using these phenomena. “We hope that it’s feasible, but in science you don’t know until you do it,” Uhlmann said. Now that the paper is published, they hope to find collaborators to build a prototype.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to University of Washington

The same freezing which is responsible for transforming liquids into glasses can help to predict some patterns observed in prime numbers, according to a team of scientists from Queen Mary, University of London and Bristol University.

At a low enough temperature, water freezes into ice by arranging its molecules into a very regular pattern called crystal. However many other liquids freeze not into crystals, but in much less regular structures called glasses – window glass being the most familiar example. Physicists have developed theories explaining the freezing phenomena, and built models for understanding the properties of glasses.

Now, a researcher from Queen Mary’s School of Mathematical Sciences, together with his colleagues from Bristol have found that frozen glasses may have something common with prime numbers and the patterns behind them.

Dr Fyodorov explained: “The prime numbers are the elements, or building blocks, of arithmetic. Our work provides evidence for a surprising connection between the primes and freezing in certain complex materials in Physics.”

A prime number is a whole number greater than 1 which can only be divided by 1 or itself. Primes play fundamentally important role in pure mathematics and its applications; and many mathematicians have tried to predict the patterns observed in prime numbers. One theory, called the Riemann Zeta Function is believed to be the most successful in revealing and explaining properties of primes.

The Riemann Zeta Function detects patterns in prime numbers in the same way that you might spot harmonies in music. It can be thought of as a series of peaks and troughs – which may be legitimately called a ‘landscape’ – encoding the properties of primes.

Dr Fyodorov continues: “One of important questions about the Riemann Zeta function relates to determining how large the highest of the peaks in the landscape are. In our paper we have argued that, unexpectedly, answering that question is related to the problem of characterizing the nature of the freezing transition in certain complex materials in Physics, such as glasses.

The team hope that understanding freezing could help mathematicians make progress in attacking some of the grand challenges of number theory.

Dr Fyodorov concludes: “Looking for connections between the statistical mechanics of random energy landscapes, random matrix theory, and the theory of the Riemann zeta function appeared to be a fruitful and promising approach.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Queen Mary, University of London

Professor Graeme Pettet is using mathematical equations to better understand how to heal wounds and bone fractures.

Understanding the way our bodies heal is not as easy as 1, 2, 3. But a Queensland University of Technology (QUT) researcher believes mathematics holds the answers to complex biological problems.

Professor Graeme Pettet, a mathematician from QUT’s Institute of Health Biomedical Innovation (IHBI), said maths could be used to better understand the structure of skin and bones and their response to healing techniques, which will eventually lead to better therapeutic innovations.

“Mathematics is the language of any science so if there are spatial or temporal variations of any kind then you can describe it mathematically,” he said.

Professor Pettet is a member of the Tissue Repair and Regeneration group, which in part focuses on growing skin in a laboratory and analysing its growth and repair process.

His team concentrates on the theoretical material, using data to build and solve mathematical equations.

“Skin is very difficult to describe. It’s very messy and very complicated. In fact most of the descriptions that engineers and biologists use are schematic stories (diagrams),” he said.

“Once we understand the structure (of the skin) and how it develops we can begin to analyse how that development impacts upon healing in the skin and maybe also diseases of the skin.”

Professor Pettet said his research would, for the first time, formalise the theories about the way cells interact when healing.

“It is clear that by improving our understanding of how the multiple cellular processes work together in a complex but orchestrated way has great potential in leading to therapeutic innovations,” he said.

Despite skin being our most accessible organ, Professor Pettet said there was a lot more to learn about how and what made it function.

“There’s a lot of structure just in the upper layer of the skin despite the fact it’s only a few cells thick,” he said.

“This can be characterised by how the cells function and change appearance, but what drives them to be that way is not completely known.

“My job is to try and understand and develop ways to describe how the bits and pieces everybody knows about are somehow connected.”

Professor Pettet is also working on applying similar techniques to figure out how to show how small, localised damage at the site of bone fractures can impact on healing.

While the long-term goal of understanding and being able to predict how our bodies heal is still a way off, Professor Pettet’s research is opening up a realm of biological problems where mathematical equations and techniques that have not previously been applied, are providing insights into the biology as well as the maths.

“We’ve discovered essentially new sets of solutions in these contexts and that’s led onto other projects looking at new mathematical tools to describe these new solutions that we’ve never seen before,” he said.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Alita Pashley, Queensland University of Technology

There’s been plenty of commentary recently on the “numeracy crisis” threatening the economies of many developed nations, including Australia.

A 2009 report by the National Academies in the US was not the first to highlight the desperate need to improve mathematical education, particularly at the K-12 level, where so many otherwise talented students either fall behind or lose interest. The report’s summary concluded:

“The new demands of international competition in the 21st century require a workforce that is competent in and comfortable with mathematics.

“There is particular concern about the chronically low mathematics and science performance of economically disadvantaged students and the lack of diversity in the science and technical workforce. Particularly alarming is that such disparities exist in the earliest years of schooling and even before school entry …”

The committee found that, although virtually all young children have the capability to learn and become competent in mathematics, the potential to learn mathematics in the early years of school is not currently realised for most.

This stems from a lack of opportunities to learn mathematics either in early childhood settings or through everyday experiences at home and in communities. And this is especially the case for the economically disadvantaged.

A UK report released last month found that millions of British adults have numerical skills at a level more commonly expected of an 11-year-old. The report also found that young people with poor numeracy skills were twice as likely to drop out of school and twice as likely to be unemployed.

The report’s authors called for a change in society’s attitude to mathematics, so that being bad at maths should no longer be seen as a “badge of honour”.

According to the same UK report, one in five of business members questioned last year said they had to teach remedial mathematics to their employees. As James Fothergill, head of education and skills at the employers’ group CSI, explained:

“It’s really important that [employees] are helped to apply maths skills and concepts in practical situations, such as being able to work out what a 30% discount is without doing it on the till.”

Many business leaders also pointed to the fact few of their employees were able to spot “rogue figures” – data that is likely to be in error.

In February this year, speaking at a forum of national educators in Canberra, Australia’s Nobel Prize-winning astronomer Brian Schmidt went so far as to warn that Australia’s resource boom was threatened by a lack of highly-trained engineers, saying:

“Too many kids who are willing and able to excel at maths are taught by teachers without the competency required to teach the subjects they are teaching.”

At the same forum, Australia’s Chief Scientist Ian Chubb said part of the problem was that mathematics and science courses were considered “boring”.

“We need to think about how to deliver the science and mathematics to a generation of students that have many more options available to them,” he said.

The situation is better elsewhere. Finland and Canada, for example, rated an “A” in an international ranking of 17 developed nations in education and skills. Finland has ranked at (or near) the top of the OECD nations in educational performance for more than ten straight years.

Canada’s strength derives in part from the system’s primary focus on K-12 education. On the other hand, Canada faces the challenge of educating and training the three million adults, in a country of under 35m people, who have only “Level 1” literacy. This would seem to show that you do get what you pay for.

Of course, other countries, such as Japan, Taiwan, China, Korea and Singapore are not standing still, with impressive gains in educational performance.

So, what can be done, for the good of everyone? Perhaps all nations can examine the educational programs of highly successful nations such as Finland.

The Finnish educational system eschews standards tests, preferring instead custom tests devised by highly qualified teachers. (Several decades ago, the government required all teachers to have master’s degrees).

Another is Finland’s focus on basic education from age seven until 16, at which point 95% of the population continues in either vocational or academic high schools. According to Pasi Sahlberg, a Finnish educator and author:

“The primary aim of education is to serve as an equalising instrument for society.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Jonathan Borwein and David H. Bailey

This is a simulation of a network of people playing Prisoner’s Dilemma. Red are cooperators; blue are defectors.

For the past twenty years, there has been a great controversy regarding whether the structure of interactions among individuals (that is, if the existence of a certain contact network or social network) helps to foment cooperation among them in situations in which not cooperating brings benefits without generating the costs of helping. Many theoretical studies have analysed this subject, but the conclusions have been contradictory since the way in which people make decisions is almost always based on a hypothesis of the models with very little basis to justify it.

The study carried out by these university researchers adopts a pioneering perspective on the theoretical study of the emergence of cooperation: rather than postulating that people make decisions according to one procedure or another, it incorporates the results obtained in experiments designed precisely to analyse how people decide whether to cooperate or not. The authors of the study are professors from the Interdisciplinary Complex Systems Group (Grupo Interdisciplinar de Sistemas Complejos – GISC) of the Mathematics Department of Carlos III University of Madrid, José Cuesta and Ángel Sánchez, together with Carlos Gracia and Yamir Moreno, from the Complex Systems and Networks Group (Grupo de Redes y Sistemas Complejos – COSNET Lab) of the Institute for Biocomputation and Physics of Complex Systems (Instituto de Biocomputación y Física de Sistemas Complejos – BIFI) of the University of Zaragoza. Their study was recently published in Scientific Reports, Nature’s new open access magazine.

This work is based on the results of an experiment carried out by the researchers and on information from other previous studies, as well as on the results (as yet unpublished) obtained from their own new experiments. The observations from these studies coincide in indicating that people do not consider what those they interact with gain; rather they think about whether or not they cooperate. In addition, their decisions usually depend on their own mood. That is, the authors noticed that the probability of cooperation occurring was considerably higher if there had been cooperation in the previous interaction. They also observed a certain heterogeneity in behaviour, finding a certain percentage of individuals who cooperated very little, regardless of what those around them did, and other individuals who almost always cooperated, again, no matter what others did.

These researchers have mathematically examined what occurs when groups of people who behave as the experiments say have to decide whether or not to cooperate, and how the existence of cooperation, globally or in the group, depends on the structure of the interactions. Specifically, the study analyses what happens if each person interacts with all of the others, if the people are placed in a square reticule and they interact with their four closest neighbours, or if they are arranged in a network that is more similar to a social network, in which the number of neighbours is highly variable and is dependent on each person. In the first case (each individual interacts with all of the others), the problem can be solved mathematically, so the level of resulting cooperation can be predicted. What the researchers observed is that this depends on the makeup of the population; that is, what proportion of the individuals use the previously described strategy, and what proportion almost always cooperates or almost never does, regardless of what the others do. Afterwards, this prediction can be compared with the results of numeric simulations obtains for the populations placed in each of the two networks, and it can be shown that the result is exactly the same, unlike what had been concluded in previous studies.

The consequences of this prediction are very important, according to the authors of the study, because if they are true, it would rule out the existence of one of the five mechanisms that have been proposed to explain the emergence of cooperation, the so-called “network reciprocity” mechanism. In order to prove the prediction, it will be necessary to carry out a large-scale experiment, something that this group of researchers in currently very involved in. These experiments are very difficult to carry out, given that studying heterogeneous networks in such a way as to obtain significant results, the team must work with hundred of volunteers simultaneously. If, as the team hopes, the experiments confirm what this study predicts, we would be witnessing a paradigm shift in the interpretation of decision-making in cooperative dilemmas: instead of considering what is to be gained, individuals would base their decisions on the cooperation they have received, and this would mean that the way that they interact (the underlying social network) would cease to be important.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Carlos III University of Madrid

This is a sample from a Spacemath@NASA problem. This diagram shows disks representing the planets discovered in orbit around eight different stars all drawn to the same scale. Earth and Jupiter are also shown for size comparison. This lesson asks the viewer to solve problems using fraction arithmetic to find out how big these new planets are compared to Earth and Jupiter.

NASA today announced that Houghton Mifflin Harcourt (HMH), Boston, has incorporated math problems developed by the SpaceMath@NASA program into some of its latest curriculum and educational products. SpaceMath uses the latest discoveries from NASA’s space science missions to develop grade-appropriate math problems spanning all of the contemporary mathematics topics areas in formal education.

“We are proud of the partnership with HMH, especially at a time when a vibrant, national science, engineering, technology, and math (STEM) education program is a major priority,” said astronomer Sten Odenwald of ADNET Systems, Inc., Lanham, Md. “SpaceMath@NASA has partnered with a major STEM education solutions provider to help students see the deep connections between math and science using NASA and space exploration as a theme.” Odenwald, who is stationed at NASA’s Goddard Space Flight Center in Greenbelt, Md., leads a team of education and public outreach (E&PO) professionals who develop the SpaceMath materials.

“Other education companies are welcome to work with SpaceMath and follow HMH’s example,” says Odenwald. “The informal partnership entails periodic consultation with the company to understand its interests and what types of content best suits its goals. We then build modules on the SpaceMath@NASA website that contain as many content requests as we can accommodate. In turn, we can offer our NASA-version of these modules for open access by all visiting teachers, while HMH is free to download those module elements to populate their own Web pages and books.”

SpaceMath products, simple one-page problems featuring a NASA discovery or engineering issue, are designed for direct classroom use by students in grades 3 through 12 using authentic, on-grade-level math topics rooted in real-world science and engineering data. It was developed in 2003 to help NASA missions upgrade their E&PO offerings by explicitly integrating mathematics problems into the science content. It was also specifically designed to meet the needs of the No Child Left Behind classroom environment where short, targeted math problems in a one-page format were now becoming the preferred method for presenting a variety of math experiences.

Problems are commonly extracted from NASA press releases and written to feature some surprising but quantifiable aspect of an image or discovery that can be paraphrased as simple mathematical problems. “These can be as diverse as a problem on fractions and percentages using Kepler exoplanet data, or as involved as determining the volume of Comet Hartley-2 using integral calculus,” said Odenwald.

“We are very excited to partner with NASA,” said Jim O’Neill, Senior Vice President, Portfolio Strategy and Marketing Management for HMH. “By incorporating the resources provided by SpaceMath@NASA into our programs, HMH can help develop students’ critical thinking skills through real-world applications that are taken from the headlines. These STEM activities also highlight the pedagogy of the Common Core for Mathematics by strengthening students’ abilities to apply concepts and integrate the Standards for Mathematical Practice.”

“Our partnership with HMH has grown out of a 10-year collaboration with them, so we consider them a major partner for future resource development,” adds Odenwald.

SpaceMath was originally funded by NASA’s E&PO programs for the IMAGE and Hinode missions. Since 2008, the program has been funded by two grants from the NASA Science Mission Directorate at NASA Headquarters, Washington – through the Research Opportunities in Space and Earth Sciences/Education and Public Outreach for Earth and Space Science (ROSES/EPOESS) program.

“Funding at the Directorate level has been crucial in allowing SpaceMath to utilize all of NASA’s press releases and extensive resources as subject matter for mathematics problems, rather than focusing exclusively on only a few NASA missions and science themes,” said Odenwald.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to NASA’s Goddard Space Flight Center