Category: Uncategorized

Like fingerprints, a firearm’s discarded shell casings have unique markings. This allows forensic experts to compare casings from a crime scene with those from a suspect’s gun. Finding and reporting a mismatch can help free the innocent, just as a match can incriminate the guilty.

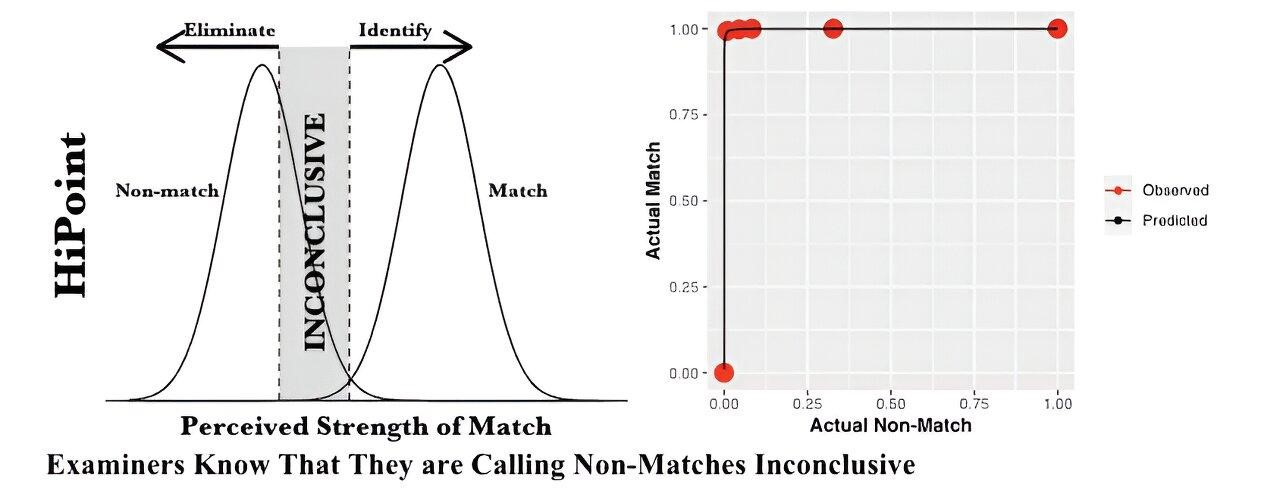
But a new study from Iowa State University researchers reveals mismatches are more likely than matches to be reported as “inconclusive” in cartridge-case comparisons.

“Firearms experts are failing to report evidence that’s favourable to the defense, and it has to be addressed and corrected. This is a terrible injustice to innocent people who are counting on expert examiners to issue a report showing that their gun was not involved but instead are left defenseless by a report that says the result was inconclusive,” says Gary Wells, an internationally recognized pioneer and scholar in eyewitness memory research.

The Distinguished Professor Emeritus co-authored the paper with Andrew Smith, associate professor of quantitative psychology. Smith studies memory, judgment and decision-making and is affiliated with both the Cognitive Psychology Program and the Psychology and Law Research group at Iowa State.

The two researchers pulled a dataset from a previously published experiment involving 228 firearms examiners and 1,811 cartridge-case comparisons. Overall, the participants were highly accurate in determining whether casings from a common firearm matched or mismatched. But when Smith and Wells applied a well-established mathematical model to the data, they found 32% of actual mismatch trials were reported as inconclusive compared to 1% of actual match trials.

“If the 16% of inconclusive reports lined up more evenly across actual matches and non-matches, we could chalk it up to human error. But the asymmetry, combined with the near-perfect performance of examiners, indicated something else was going on. They almost certainly knew that most of the cases they called inconclusive were actual mismatches,” says Smith.

Asking the wrong question

The researchers say a flawed response scale could help explain the dissociation between what examiners know and what they report.

Currently, the Association of Firearm and Tool Mark Examiners’ Conclusion Scale asks forensic firearms experts whether the crime-scene casings and casings from the suspect’s gun are from the same source. Smith and Wells say the problem with the “source” question is that it’s possible for a mismatch to be attributable to an altered firearm or degraded evidence.

With these possible explanations, Smith and Wells say some examiners might take the position that it is never appropriate to call something a mismatch and instead default to calling the results inconclusive.

“Instead of asking examiners to make source determinations, examiners should simply be asked if the shell casings from the suspect’s gun match the casings found at the crime scene. Asking if the casings match or not and to what degree could provide more transparency,” says Smith.

Questions about alterations and degradation could be asked separately, Smith adds.

Wells emphasizes that until the response scale is fixed, defense lawyers should cross-examine forensic firearms experts who claim inconclusive results. They need to “show their work,” he says. Wells also recommends getting a second opinion if the cartridge-case comparison report comes back as inconclusive.

Bias in the lab

The researchers say another possible explanation for calling a result inconclusive when it’s actually a mismatch is “adversarial allegiance bias.”

“Most forensic firearm examiners and their labs are retained by the prosecution or police departments,” says Smith. “Some examiners might render reports that are inconclusive despite the mismatch because they don’t want to hurt the side that’s essentially their employer.”

Smith and Wells say this type of bias can also occur at the lab level. They point to survey data showing some labs have policies that do not allow examiners to report mismatches.

“It’s hard to get rid of bias but fixing the response scale would go a long way in solving the problem,” says Wells. “In the meantime, there are likely past cases that need relitigated.”

The researchers underscore that forensic science needs to be proficient in not just incriminating the guilty but also in freeing the innocent from suspicion. Minimizing bias and improving transparency in cartridge-case comparisons will help create a more fair and efficient criminal justice system.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Iowa State University

In a remarkable breakthrough in the field of mathematical science, Professor Kyudong Choi from the Department of Mathematical Sciences at UNIST has provided an irrefutable proof that certain spherical vortices exist in a stable state. This discovery holds significant implications for predicting weather anomalies and advancing weather prediction technologies. The research is published in the journal Communications on Pure and Applied Mathematics.

A vortex is a rotating region of fluid, such as air or water, characterized by intense rotation. Common examples include typhoons and tornadoes frequently observed in news reports. Professor Choi’s mathematical proof establishes the stability of specific types of vortex structures that can be encountered in real-world fluid flows.

The study builds upon the foundational Euler equation formulated by Leonhard Euler in 1757 to describe the flow of eddy currents. In 1894, British mathematician M. Hill mathematically demonstrated that a ball-shaped vortex could maintain its shape indefinitely while moving along its axis.

Professor Choi’s research confirms that Hill’s spherical vortex maximizes kinetic energyunder certain conditions through the application of variational methods. By incorporating functional analysis and partial differential equation theory from mathematical analysis, this study extends previous investigations on two-dimensional fluid flows to encompass three-dimensional fluid dynamics with axial symmetry conditions.

One notable feature identified by Hill is the presence of strong upward airflow at the front of the spherical vortex—an attribute often observed in phenomena like typhoons and tornadoes. Professor Choi’s findings serve as a starting point for further studies involving measurements related to residual time associated with these ascending air currents.

“Research on vortex stability has gained international attention,” stated Professor Choi. “And it holds long-term potential for advancements in today’s weather forecasting technology.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to JooHyeon Heo, Ulsan National Institute of Science and Technology

Tens of thousands of handwritten pages by one of the 20th century’s greatest mathematicians, Alexander Grothendieck, many of which the eccentric genius penned while living as a hermit, were unveiled in France on Friday.

The unpublished manuscripts, which veer from math to metaphysics, autobiography and even long musings on Satan, offer a unique insight into the enigmatic mind of the French mathematician, according to experts at the Paris library where they were donated.

Grothendieck, who died aged 86 in 2014, is considered by some to have revolutionized the field of mathematics in the way that Einstein did for physics. His work on algebraic geometry earned him the 1966 Fields Medal, known as the Nobel prize of the math world.

At that time Grothendieck was already a radical environmentalist and pacifist. But he withdrew from the world almost entirely in the early 1990s, in part to focus on what he referred to as his “scribblings”.

While living as a hermit in the southern French village of Lasserre he frantically wrote “Reflections on Life and the Cosmos,” one of the two main works added to the collection of the National Library of France (BnF) on Friday.

The massive tome includes 30,000 pages across 41 different volumes covering science, philosophy and psychology—all densely scribbled with a fountain pen.

The second work, “The Key to Dreams or Dialogue with the Good Lord,” is a typed manuscript in which he explores the interpretation of dreams.

These pages, which have previously circulated online, were written between 1987-1988.

‘Completely cut ties’

At that time, Grothendieck remained a professor at the University of Montpellier but had largely withdrawn from the mathematical community.

He became a recluse when he moved to Lasserre.

“He completely cut ties with his family, we could no longer communicate with him,” his daughter Johanna Grothendieck told AFP.

“When we sent him a letter, it was returned to sender,” said Johanna, a 64-year-old ceramic artist who traveled from southwest France to attend the ceremony at the library.

“Writing was his main activity,” she added.

Towards the end of Grothendieck’s life, a neighbour told his family that his health was deteriorating.

Johanna and one of her brothers were finally able to visit their father. It was than that they discovered “Reflections on Life and the Cosmos,” which was meticulously catalogued in his library.

In his 1997 will, Grothendieck left the early sections of the tome to the BnF. Now his children have donated the rest.

“It was an extremely important work in his eyes. He even wanted to create a foundation to look after it,” Johanna Grothendieck said.

‘Ghosts of his past’

Jocelyn Monchamp, a curator an the BnF, said the manuscripts were unique because they covered so many subjects at the same time yet formed a whole with “undeniable literary qualities”.

This is particularly the case for the autobiographical volume “Harvest and Sowing”, which depicts the author “in a metaphysical retreat,” she said.

Monchamp has spent a month poring over the writing, trying to decipher the dense fountain pen text.

“I became used to it,” she said, adding that at least Grothendieck methodically wrote the numbers and dates on all the pages.

In one of the sections, “Structures of the Psyche,” enigmatic diagrams translate psychology into the language of algebra.

In another, “The Problem of Evil,” Grothendieck muses over 15,000 pages on metaphysics and Satan.

One gets the feeling of a man “overtaken by the ghosts of his past,” Johanna Grothendieck said.

The mathematician’s father fled Germany during World War II, only to be handed by the Vichy France government to the Nazis and die at the Auschwitz concentration camp. Experts expect it will take some time to fully understand Grothendieck’s writing. On Friday, the collection joined the manuscript department of the BnF, where it will only be accessible to researchers.

During the donation ceremony, one of the volumes was placed in a glass case next to a manuscript by ancient Greek mathematician Euclid, considered the father of geometry.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Juliette Collen

Understanding how children learn to count can have profound impacts on the kinds of instructional materials used in the classroom. And the way those materials are designed can shape the strategies children use to learn, according to a new paper led by Concordia researchers.

Writing in the journal School Science and Mathematics, the authors study how young children, mostly in the first grade, used a hundreds table to perform age-appropriate counting tasks. Hundreds tables, as the name suggests, are charts divided into rows and columns of 10, with each square containing a number from one to 100. The researchers discovered that the children who counted left-to-right, top-to-bottom outperformed children who counted left-to-right, bottom-to-top.

In this study, children used the tables on a screen to solve addition problems. One group of children used a top-down table, where the top left corner was marked 1 and bottom left corner was marked 100. Another group of children used a bottom-up, where one occupied the bottom left and 100 the top right. A third group of children used a bottom-up table with a visual cue of a cylinder next to it. The cylinder was designed to show the “up-is-more” relation as it filled with water when the numbers increased when moving up in the table.

“We found that children using the top-down chart used a more sophisticated strategy of counting by 10 and moving vertically, rather than using the more simplistic strategy of counting by one and moving horizontally,” says Vera Wagner. She co-authored the paper with Helena Osana, a professor in the Department of Education in the Faculty of Arts and Science and Jairo Navarrete-Ulloa of O’Higgins University in Chile.

The authors believe the benefits of the top-down table could be related to the way children learn to read and that they are applying the same approach to base-ten concepts.

“We were working with young children, so reading instruction is likely at the forefront of their attention,” says Wagner, who now teaches elementary students at a Montreal-area school. “The structure of moving in that particular way might be more ingrained.”

The power of spatial configuration

Osana notes that the practice of counting by 10s rather than by ones—which is a more efficient method of arriving at the same answer—is an example of unitizing, in which multiples of one unit form a new unit representing a larger number.

“From a theoretical perspective, the study shows that the spatial configuration of instructional materials can actually support this more sophisticated understanding of numbers and the unitizing aspect that goes along with it,” she says.

While the researchers are not suggesting children will automatically gravitate toward the top-down chart under every circumstance, they do think the study’s results provide educators with a sense of the ways their students process numbers and addition.

“It is important for teachers to be aware of how children are thinking about the tools we are giving them,” says Osana, principal investigator of the Mathematics Teaching and Learning Lab. “We are not saying that teachers have to use the top-down hundreds chart every time, but they should think about the strategies their students are using and why they use them with one particular instructional tool and not another.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Patrick Lejtenyi, Concordia University

It seems there’s a five-letter word describing what many players of the wildly popular Wordle puzzle do daily as they struggle to find a target word within six tries.

According to one mathematics expert, that word is “cheat.”

James P. Dilger, who by day is professor emeritus at Stony Brook University in New York specializing in the mechanisms of anesthetic action, and by night is a Wordle junkie, says the numbers behind published Wordle success rates don’t quite add up.

Wordle was developed by a software engineerto pass the time during the early days of COVID restrictions. Players must determine a target five-letter word in six or fewer attempts. With each guess, the player is provided with three bits of information: correct letters in the correct position are displayed in green, correct letters placed in incorrect spots are displayed in yellow, and incorrect letters are displayed in black.

In the beginning, Wordle was played mainly among family and friends of the developer, Josh Wardle. Wordle’s popularity soared, reaching 3 million users after The New York Times purchased the game in January 2022. Today, some 2 million play Wordle daily. It is recreated in 50 languages globally.

Dilger’s suspicions arose while studying the game’s statistics published daily by The Times.

“I noticed one day an awful lot of people answered with one guess and thought, ‘that’s strange,'” Dilger said. “And then I paid attention to it and it was happening day after day. Well, I’m a science nerd and wanted to know what’s going on.”

Dilger imported statistics covering four months of user guesses into an Excel spreadsheet. His report, “Wordle: A Microcosm of Life. Luck, Skill, Cheating, Loyalty, and Influence!” appeared in the preprint server arXiv Sept. 6.

The game has a data bank containing 2,315 words, good for five years of play. (There actually are more than 12,000 five-letter words in the English language, but The Times weeded out the most obscure ones.)

Dilger calculated that the odds of randomly guessing the day’s word at 0.043%, totaling 860 players. Yet, Times statistics show that the number of players making correct first guesses in each game never dipped below 4,000.

“Do I mean to tell you that never, not once, was the share percent of the first guess less than 0.2%? Yup!” Dilger asserted.

He went further. His numbers are based on the 2,315-word master list compiled by The Times, but 800 of those words have already been used. Most players are not likely to know that detail, but if they did, and they excluded words already played, their odds of guessing the correct word would rise slightly. Yet, according to Dilger, their odds would still be a low 0.066%.

“Yet, it happens consistently every day,” Dilger said. “Some days it’s as high as 0.5%,” which would be 10,000 players.

He also noted how unlikely it would be that a user would correctly guess such poor first-choice candidates as “nanny” and “igloo.” Players gain maximum advantage when they surmise words with non-repeating characters and as many vowels as possible. “Nanny” repeats one letter three times and uses only two vowels. “Igloo” not only is a relatively rare word, but contains only two vowels, repeating one of them.

“What shall we call these people?” He asked. “‘Cheaters’ comes to mind, so that’s what I call ’em.”

Dilger did not offer any explanation for such nefarious behaviour, other than to say that many players “became frustrated at some point in the game and then felt joy or relief after having surpassed the hurdle with a cheat.”

“We are baffled as to how first-word cheaters actually have fun playing,” Dinger said, “but that does not diminish our enjoyment of the game.”

He might have quoted former wrestler, actor, philosopher and governor of Minnesota Jesse Ventura, who once suggested, “Winners never cheat, and cheaters never win.” Except maybe in Wordle.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Peter Grad, Phys.org

A major new study has revealed that American teenagers are more likely than any other nationality to brag about their math ability.

Research using data from 40,000 15-year-olds from nine English-speaking nations internationally found those in North America were the most likely to exaggerate their mathematical knowledge, while those in Ireland and Scotland were least likely to do so.

The study, published in Assessment in Education: Principles, Policy & Practice, used responses from the OECD Programme for International Student Assessment (PISA), in which participants took a two-hour math test alongside a 30-minute background questionnaire.

They were asked how familiar they were with each of 16 mathematical terms—but three of the terms were fake.

Further questions revealed those who claimed familiarity with non-existent mathematical concepts were also more likely to display overconfidence in their academic prowess, problem-solving skills and perseverance.

For instance, they claimed higher levels of competence in calculating a discount on a television and in finding their way to a destination. Two thirds of those most likely to overestimate their mathematical ability were confident they could work out the petrol consumption of a car, compared to just 40% of those least likely to do so.

Those likely to over-claim were also more likely to say if their mobile phone stopped sending texts they would consult a manual (41% versus 30%) while those less likely to do so tended to say they would react by pressing all the buttons (56% versus 49%).

Over-claimers were also more likely to say they were popular with their peers at school, although the evidence was less strong on this topic.

Overall, boys were more likely to overclaim than girls, and those from advantaged backgrounds were more likely to do so than those from less advantaged groups. In most countries, immigrants were more likely to do this than the native-born, particularly in Northern Ireland and New Zealand although not in the United States.

Three broad clusters of countries emerged, with the United States and Canada at the top of the rankings when it came to excessive claims on math knowledge, and with Ireland, Northern Ireland and Scotland at the bottom. In the middle were Australia, New Zealand, England and Wales.

The report’s lead author is John Jerrim, Professor of Education and Social Statistics at the UCL Institute of Education. “Our research provides important new insight into how those who over-claim about their math ability also exhibit high levels of over-confidence in other areas,” he said.

“Although ‘overclaiming’ may at first seem to be a negative social trait, we have previously found that overconfident individuals are more likely to land top-jobs. The fact that young men tend to overclaim their knowledge more than young women, and the rich are more likely to overclaim than the poor, could be related to the different labor market outcomes of these groups.”

Students were shown a list of 16 items and asked to indicate their knowledge of each on a five-point scale ranging from “never heard of it” to “know it well, understand the concept.” They were:

1. Exponential function
2. Divisor
3. Quadratic function
4. Proper number
5. Linear equation
6. Vectors
7. Complex number
8. Rational number
9. Radicals
10. Subjunctive scaling
11. Polygon
12. Declarative fraction
13. Congruent figure
14. Cosine
15. Arithmetic mean
16. Probability

Numbers 4, 10 and 12 were fake terms.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Taylor & Francis

Richard Schwartz, a mathematician at Brown University has found a solution to the problem of how small a Möbius band can be made without intersecting itself—at least for a smooth piece of paper. The paper is published on the arXiv preprint server.

A Möbius strip (or band) is both a physical and mathematical object. A sample can be constructed by twisting a simple strip of paper one time and then taping the ends together. Since they were first discovered back in the mid-1800s, mathematicians have been scratching their heads trying to determine one simple constraint—what is the shortest strip necessary for making one? Back in the late 1970s, a pair of mathematicians, Charles Sidney Weaver and Benjamin Rigler Halpern, found that the problem could be made simpler by allowing self-intersections—that changed the problem to one that involved seeking the minimum amount of strip needed to avoid self-intersections.

Four years ago, Schwartz found himself intrigued by the problem and, as he describes in his paper, became “hooked” on finding a solution. Two years ago, he thought he had finally found it and published a proof showing his work—it involved breaking down the problem into multiple pieces and then using geometry principles to solve the puzzle as a whole.

Unfortunately, there turned out to be a major flaw in his work that he did not discover until much more recently. He found it by creating physical samples and cutting them in different ways to see how they worked on a deeper level. He discovered that the 2D strip was not shaped like a parallelogram as had been thought—instead, it was a trapezoid.

Inspired by his discovery, he went back to this original proof and corrected the error, and in doing so, found that the proof worked much better than it had originally. It was also much simpler. He also used the proof to work out the optimization problem, and got what he was hoping for: √3. He notes that while pleased with his own work, he has already turned his attention to another problem—to determine how short a band can be if it is twisted three times instead of once.\

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Bob Yirka, Phys.org

For much of her teaching career, Carrie Stark relied on math games to engage her students, assuming they would pick up concepts like multiplication by seeing them in action. The kids had fun, but the lessons never stuck.

A few years ago, she shifted her approach, turning to more direct explanation after finding a website on a set of evidence-based practices known as the science of math.

“I could see how the game related to multiplication, but the kids weren’t making those connections,” said Stark, a math teacher in the suburbs of Kansas City. “You have to explicitly teach the content.”

As American schools work to turn around math scores that plunged during the pandemic, some researchers are pushing for more attention to a set of research-based practices for teaching math. The movement has passionate backers, but is still in its infancy, especially compared with the phonics-based “science of reading” that has inspired changes in how classrooms across the country approach literacy.

Experts say math research hasn’t gotten as much funding or attention, especially beyond the elementary level. Meanwhile, the math instruction schools are currently using doesn’t work all that well. The U.S. trails other high-income countries in math performance, and lately more students graduate high school with deficits in basic math skills.

Advocates say teaching practices supported by quantitative research could help, but they are still coming into focus.

“I don’t think the movement has caught on yet. I think it’s an idea,” said Matthew Burns, a professor of special education at the University of Florida who was among researchers who helped create a Science of Math website as a resource for teachers.

WHAT IS THE SCIENCE OF MATH?

There’s a debate over which evidence-based practices belong under the banner of the science of math, but researchers agree on some core ideas.

The foremost principle: Math instruction must be systematic and explicit. Teachers need to give clear and precise instructions and introduce new concepts in small chunks while building on older concepts. Such approaches have been endorsed by dozens of studieshighlighted by the Institute of Education Sciences, an arm of the U.S. Education Department that evaluates teaching practices.

That guidance contrasts with exploratory or inquiry-based models of education, where students explore and discover concepts on their own, with the teacher nudging them along. It’s unclear which approaches are used most widely in schools.

In some ways, the best practices for math parallel the science of reading, which emphasizes detailed, explicit instruction in phonics, instead of letting kids guess how to read a word based on pictures or context clues. After the science of reading gained prominence, 18 states in just three years have passed legislation mandating that classroom teachers use evidence-backed methods to teach reading.

Margie Howells, an elementary math teacher in Wheeling, West Virginia, first went researching best practices because there weren’t as many resources for dyscalculia, a math learning disability, as there were for dyslexia. After reading about the science of math movement, she became more explicit about things that she assumed students understood, like how the horizontal line in a fraction means the same thing as a division sign.

“I’m doing a lot more instruction in vocabulary and symbol explanations so that the students have that built-in understanding,” said Howells, who is working on developing a science-based tutoring program for students with dyscalculia and other learning differences.

THE SO-CALLED MATH WARS

Some elements of math instruction emphasize big-picture concepts. Others involve learning how to do calculations. Over the decades, clashes between schools of thought favouring one or another have been labeled the “math wars.” A key principle of the science of math movement is that both are important, and teachers need to foster procedural as well as conceptual understanding.

“We need to be doing all those simultaneously,” Stark said.

When Stark demonstrates a long division problem, she writes out the steps for calculating the answer while students use a chart or blocks to understand the problem conceptually.

Stark helps coach fellow teachers at her school to support struggling students—something she used to feel unequipped to do, despite 20 years of teaching experience. Most of the resources she found online just suggested different math games. So, she did research online and signed up for special trainings, and started focusing more on fundamentals.

For one fifth grader who was struggling with fractions, she explicitly re-taught equivalent fractions from third grade—why two-fourths are the same as one-half, for instance. He had been working with her for three years, but this was the first time she heard him say, “I totally get it now!”

“He was really feeling success. He was super proud of himself,” Stark said.

Still, skeptics of the science of math question the emphasis placed on learning algorithms, the step-by-step procedures for calculation. Proponents say they are necessary along with memorization of math facts (basic operations like 3×5 or 7+9) and regular timed practice—approaches often associated with mind-numbing drills and worksheets.

Math is “a creative, artistic, playful, reasoning-rich activity. And it’s very different than algorithms,” said Nick Wasserman, a professor of math education at Columbia University’s Teachers College.

Supporters argue mastering math facts unlocks creative problem-solving by freeing up working memory—and that inquiry, creativity and collaboration are still all crucial to student success.

“When we have this dichotomy, it creates an unnecessary divide and it creates a dangerous divide,” said Elizabeth Hughes, a professor of special education at Penn State and a leader in the science of math movement. People feel the need to choose sides between “Team Algorithms” and “Team Exploratory,” but “we really need both.”

A HIGHER IMPORTANCE ON READING?

Best practices are one thing. But some disagree such a thing as a “science of math” exists in the way it does for reading. There just isn’t the same volume of research, education researcher Tom Loveless said.

“Reading is a topic where we have a much larger amount of good, solid, causal research that can link instruction to student achievement,” he said.

To some, the less advanced state of research on math reflects societal values, and how many teachers themselves feel more invested in reading. Many elementary school teachers doubt their own math ability and struggle with anxiety around teaching it.

“Many of us will readily admit that we weren’t good at math,” said Daniel Ansari, a professor of cognitive neuroscience at Western University in Canada. “If I was illiterate, I wouldn’t tell a soul.”

Still, Ansari said, there is enough research out there to make a difference in the classroom.

“We do understand some of the things that really work,” he said, “and we know some of the things that are not worth spending time on.”

Correction note: This story has been corrected to reflect that Burns is now at the University of Florida, and not the University of Missouri.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Sharon Lurye

Getting in sync can be exhilarating when you’re dancing in rhythm with other people or clapping along in an audience. Fireflies too know the joy of synchronization, timing their flashes together to create a larger display to attract mates.

Synchronization is important at a more basic level in our bodies, too. Our heart cells all beat together (at least when things are going well) and synchronized electrical waves can help coordinate brain regions—but too much synchronization of brain cells is what happens in an epileptic seizure.

Sync most often emerges spontaneously rather than through following the lead of some central timekeeper. How does this happen? What is it about a system that determines whether sync will emerge, and how strong it will be?

In new research published in Proceedings of the National Academy of Sciences, we show how the strength of synchronization in a network depends on the structure of the connections between its members—whether they be brain cells, fireflies, or groups of dancers.

The science of sync

Scientists originally became interested in sync to understand the inner workings of natural systems. We have also become interested in designing sync as a desired behaviour in human-made systems such as power grids (to keep them in phase).

Mathematicians can analyse sync by treating the individuals in the system as “coupled oscillators.” An oscillator is something that periodically repeats the same pattern of activity, like the sequence of steps in a repetitive dance, and coupled oscillators are ones that can influence each other’s behaviour.

It can be useful to measure whether a system of oscillators can synchronize their actions, and how strong that synchronization would be. Strength of synchronization means how well the sync can recover from disturbances.

Take a group dance, for example. A disturbance might be one person starting to get some steps wrong. The person might quickly recover by watching their friends, they might throw their friends off for a few steps before everyone recovers, or in the worst case it might just cause chaos.

Synced systems are strong but hard to unravel

Two factors make it difficult to determine how strong the synchronization in a set of coupled oscillators could be.

First, it’s rare for a single oscillator to be in charge and telling everyone else what to do. In our dance example, that means there’s neither music nor lead dancers to set the tempo.

And second, usually each oscillator is only connected to a few others in the system. So each dancer can only see and react to a few others, and everyone is taking their cues from a completely different set of dancers.

This is the case in the brain, for example, where there is a complex network structure of connections between different regions.

Real complex systems like this, where there is no central guiding signal and oscillators are connected in a complex network, are very robust to damage and adaptable to change, and can more easily scale to different sizes.

Stronger sync comes from more wandering walks

One drawback of such complicated systems is for scientists, as they are mathematically difficult to come to grips with. However, our new research has made a significant advance on this front.

We have shown how the network structure connecting a set of oscillators controls how well they can synchronize. The quality of sync depends on “walks” on a network, which are sequences of hops between connected oscillators or nodes.

Our math examines what are called “paired walks.” If you start at one node and take two walks with randomly chosen next hops for a specific number of hops, the two walks might end up at the same node (these are convergent walks) or at different nodes (divergent walks).

We found that the more often paired walks on a network were convergent rather than divergent, the worse the synchronization on the network would be.

When more paired walks are convergent, disturbances tend to be reinforced.

In our dancing example, one person making the wrong steps might lead some neighbours astray, who may then lead some of their neighbours astray and so on.

These chains of potential disturbances are like walks on the network. When those disturbances propagate through multiple neighbours and then converge on one person, that person is going to be much more likely to copy the out-of-sync moves than if only one of their neighbours was offbeat.

Social networks, power grids and beyond

So networks with many convergent walks are prone to poorer synchronization. This is good news for the brain avoiding epilepsy, as its highly modular structure brings a high proportion of convergent walks.

We can see this reflected in the echo chamber phenomenon in social media. Tightly coupled subgroups reinforcing their own messages can synchronize themselves well, but may fall far out of step with the wider population.

Our results bring a new understanding to how synchronization functions in different natural network structures. It opens new opportunities in terms of designing network structures or interventions on networks, either to aid synchronization (in power grids, say) or to avoid synchronization (say in the brain).

More widely, it represents a major step forward in our understanding of how the structure of complex networks affects their behaviour and capabilities.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Joseph Lizier, The Conversation

Knots are used in all sorts of ways, every day. They ensure safety both indoors and for outdoor activities such as boating or sailing, are used as surgical sutures, as decorations, and they can even be found at nanoscales in nature, for example in DNA molecules.

Elastic knots are those that bounce back into their original shape in the absence of friction. There are open elastic knots tied with a single length of wire with two ends, which revert to being a straight line, and closed elastic knots in which the ends of the wire used to tie them have been attached together. These tend to spring back into a curved shape.

With a focus on closed knots, researchers in the Ecole Polytechnique Federale de Lausanne Geometric Computing Laboratory, led by Professor Mark Pauly, along with colleagues in Canada and the United States, have discovered thousands of new transformable knots including three novel shapes that the humble figure-eight knot can assume, doubling the number documented to date in scientific literature.

The findings are published in the journal ACM Transactions on Graphics.

To make these discoveries, the team first developed a computational pipeline that combines randomized spatial sampling and physics simulation to efficiently find the stable equilibrium states of elastic knots. Leveraging results from knot theory, they ran their pipeline on thousands of different topological knot types to create an extensive data set of multistable knots.

“By applying a series of filters to this data, we discovered new transformable knots with interesting physical properties and beautiful geometric forms,” explained doctoral assistant Michele Vidulis, the lead author of the paper “Computational Exploration of Multistable Elastic Knots.”

“This rich set of fascinating shapes can be created simply by knotting an elastic wire, and we noticed how such seemingly simple objects can sometimes exhibit tens or even hundreds of different stable shapes. The novel geometric patterns we identified were at times surprising. For example, we found that most—but not all—the preferred shapes of elastic knots are flat and planar, while few of them assume three-dimensional shapes,” Vidulis continued.

The team conducted further analysis across knot types that revealed new geometric and topological patterns with constructive principles not seen in previously tabulated knot types, showing how multistable elastic knots might be used to design new structures.

“As a result of our research, we can see elastic knots being used in the design process of self-deployable structures, like pop-up tents or lightweight emergency shelters. New metamaterials can be designed that combine several elastic knotted elements to build a network with complex mechanical behaviour,” Vidulis explained.

The team also created engaging recreational puzzles with the challenge to deform an elastic knot and manually find some of the interesting geometric shapes that they have computed with their algorithms.

As satisfying as these new discoveries are, Vidulis and the team believe that the work opens the way to several other potential new research directions.

“We want to explore the design of self-deployable structures and consider coupling elastic rods with fabric materials. As well, despite simulating thousands of different knots, our exploration only scratched the surface of the millions of knots that are known. We also plan to study more complex ensembles of knotted systems, in which new mechanical properties might emerge from the way in which the individual components are intertwined to each other,” he concluded.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to anya Petersen, Ecole Polytechnique Federale de Lausanne