Author: IMC

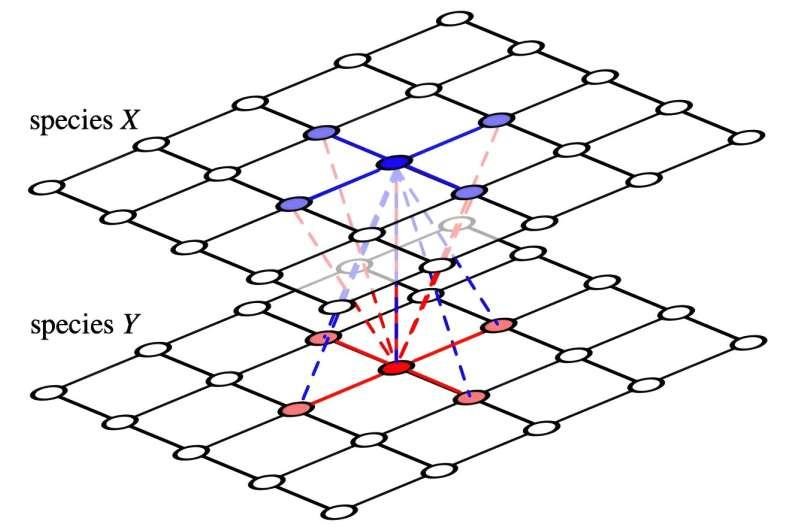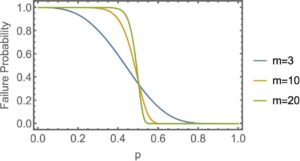
Phase Transition. The probability for the poll to fail, 𝜋₀, plotted as a function of p, the fraction of time slots that each respondent is available. Credit: The European Physical Journal B (2024). DOI: 10.1140/epjb/s10051-024-00742-z

In a world where organizing a simple meeting can feel like herding cats, new research from Case Western Reserve University reveals just how challenging finding a suitable meeting time becomes as the number of participants grows.

The study, published in the European Physical Journal B, dives into the mathematical complexities of this common task, offering new insights into why scheduling often feels so impossible.

“If you like to think the worst about people, then this study might be for you,” quipped researcher Harsh Mathur, professor of physics in the College of Arts and Sciences at CWRU. “But this is about more than Doodle polls. We started off by wanting to answer this question about polls, but it turns out there is more to the story.”

Researchers used mathematical modeling to calculate the likelihood of successfully scheduling a meeting based on several factors: the number of participants (m), the number of possible meeting times (τ) and the number of times each participant is unavailable (r).

What they found was that as the number of participants grows, the probability of scheduling a successful meeting decreases sharply.

Specifically, the probability drops significantly when more than five people are involved—especially if participant availability remains consistent.

“We wanted to know the odds,” Mathur said. “The science of probability actually started with people studying gambling, but it applies just as well to something like scheduling meetings. Our research shows that as the number of participants grows, the number of potential meeting times that need to be polled increases exponentially.

“The project had started half in jest but this exponential behaviour got our attention. It showed that scheduling meetings is a difficult problem, on par with some of the great problems in computer science.”

Interestingly, researchers found a parallel between scheduling difficulties and physical phenomena. They observed that as the probability of a participant rejecting a proposed meeting time increase, there’s a critical point where the likelihood of successfully scheduling the meeting drops sharply.

It’s a phenomenon similar to what is known as “phase transitions” in physics, Mathur said, such as ice melting into water.

“Understanding phase transitions mathematically is a triumph of physics,” he said. “It’s fascinating how something as mundane as scheduling can mirror the complexity of phase transitions.”

Mathur also noted the study’s broader implications, from casual scenarios like sharing appetizers at a restaurant to more complex settings like drafting climate policy reports, where agreement among many is needed.

“Consensus-building is hard,” Mathur said. “Like phase transitions, it’s complex. But that’s also where the beauty of mathematics lies—it gives us tools to understand and quantify these challenges.”

Mathur said the study contributes insights into the complexities of group coordination and decision-making, with potential applications across various fields.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Case Western Reserve University

A model developed by evolutionary mathematicians in Canada and Europe shows that as cooperation becomes easier, it can unexpectedly break down. The researchers at the University of British Columbia and Hungarian Research Network used computational spatial models to arrange individuals from the two species on separate lattices facing one another. Credit: Christoph Hauert and György Szabó

Darwin was puzzled by cooperation in nature—it ran directly against natural selection and the notion of survival of the fittest. But over the past decades, evolutionary mathematicians have used game theory to better understand why mutual cooperation persists when evolution should favour self-serving cheaters.

At a basic level, cooperation flourishes when the costs to cooperation are low or the benefits large. When cooperation becomes too costly, it disappears—at least in the realm of pure mathematics. Symbiotic relationships between species—like those between pollinators and plants–are more complex but follow similar patterns.

But new modeling published today in PNAS Nexus adds a wrinkle to that theory, indicating that cooperative behaviour between species may break down in situations where, theoretically at least, it should flourish.

“As we began to improve the conditions for cooperation in our model, the frequency of mutually beneficial behaviour in both species increases, as expected,” says Dr. Christoph Hauert, a mathematician at the University of British Columbia who studies evolutionary dynamics.

“But as the frequency of cooperation in our simulation gets higher—closer to 50%—suddenly there’s a split. More cooperators pool in one species and fewer in the other—and this asymmetry continues to get stronger as the conditions for cooperation get more benign.”

While this “symmetry breaking of cooperation” between two populations has been modeled by mathematicians before, this is the first model that enables individuals in each group to interact and join forces in a more natural way.

Dr. Hauert and colleague Dr. György Szabó from the Hungarian Research Network used computational spatial models to arrange individuals from the two species on separate lattices facing one another. This enables cooperators to form clusters and reduce their exposure to (and exploitation by) cheaters by more frequently interacting with other cooperators.

“Because we chose symmetric interactions, the level of cooperation is the same in both populations,” says Dr. Hauert. “Clusters can still form and protect cooperators but now they need to be synchronized across lattices because that’s where the interactions occur.”

“The odd symmetry breaking in cooperation shows parallels to phase transitions in magnetic materials and highlights the success of approaches developed in statistical and solid state physics,” says Dr. Szabó.

“At the same time the model sheds light on spikes in dramatic changes in behaviour that can significantly affect the interactions in complex living systems.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to University of British Columbia

When solving a mathematical problem, it is possible to appeal to the ordinal property of numbers, i.e. the fact

The way we memorize information—a mathematical problem statement, for example—reveals the way we process it. A team from the University of Geneva (UNIGE), in collaboration with CY Cergy Paris University (CYU) and Bourgogne University (uB), has shown how different solving methods can alter the way information is memorized and even create false memories.

By identifying learners’ unconscious deductions, this study opens up new perspectives for mathematics teaching. These results are published in the Journal of Experimental Psychology: Learning, Memory, and Cognition.

Remembering information goes through several stages: perception, encoding—the way it is processed to become an easily accessible memory trace—and retrieval (or reactivation). At each stage, errors can occur, sometimes leading to the formation of false memories.

Scientists from the UNIGE, CYU and Bourgogne University set out to determine whether solving arithmetic problems could generate such memories and whether they could be influenced by the nature of the problems.

Unconscious deductions create false memories

When solving a mathematical problem, it is possible to call upon either the ordinal property of numbers, i.e., the fact that they are ordered, or their cardinal property, i.e., the fact that they designate specific quantities. This can lead to different solving strategies and, when memorized, to different encoding.

In concrete terms, the representation of a problem involving the calculation of durations or differences in heights (ordinal problem) can sometimes allow unconscious deductions to be made, leading to a more direct solution. This is in contrast to the representation of a problem involving the calculation of weights or prices (cardinal problem), which can lead to additional steps in the reasoning, such as the intermediate calculation of subsets.

The scientists therefore hypothesized that, as a result of spontaneous deductions, participants would unconsciously modify their memories of ordinal problem statements, but not those of cardinal problems.

To test this, a total of 67 adults were asked to solve arithmetic problems of both types, and then to recall the wording in order to test their memories. The scientists found that in the majority of cases (83%), the statements were correctly recalled for cardinal problems.

In contrast, the results were different when the participants had to remember the wording of ordinal problems, such as: “Sophie’s journey takes 8 hours. Her journey takes place during the day. When she arrives, the clock reads 11. Fred leaves at the same time as Sophie. Fred’s journey is 2 hours shorter than Sophie’s. What time does the clock show when Fred arrives?”

In more than half the cases, information deduced by the participants when solving these problems was added unintentionally to the statement. In the case of the problem mentioned above, for example, they could be convinced—wrongly—that they had read: “Fred arrived 2 hours before Sophie” (an inference made because Fred and Sophie left at the same time, but Fred’s journey took 2 hours less, which is factually true but constitutes an alteration to what the statement indicated).

“We have shown that when solving specific problems, participants have the illusion of having read sentences that were never actually presented in the statements, but were linked to unconscious deductions made when reading the statements. They become confused in their minds with the sentences they actually read,” explains Hippolyte Gros, former post-doctoral fellow at UNIGE’s Faculty of Psychology and Educational Sciences, lecturer at CYU, and first author of the study.

Invoking memories to understand reasoning

In addition, the experiments showed that the participants with the false memories were only those who had discovered the shortest strategy, thus revealing their unconscious reasoning that had enabled them to find this resolution shortcut. On the other hand, the others, who had operated in more stages, were unable to “enrich” their memory because they had not carried out the corresponding reasoning.

“This work can have applications for learning mathematics. By asking students to recall statements, we can identify their mental representations and therefore the reasoning they used when solving the problem, based on the presence or absence of false memories in their restitution,” explains Emmanuel Sander, full professor at the UNIGE’s Faculty of Psychology and Educational Sciences, who directed this research.

It is difficult to access mental constructs directly. Doing so indirectly, by analysing memorization processes, could lead to a better understanding of the difficulties encountered by students in solving problems, and provide avenues for intervention in the classroom.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article to be given University of Geneva

All a_i lie on the same sheet of a cone with vertex x. The right-hand picture is not true to scale relative to the given numerical example. Credit: Advances in Applied Mathematics (2024). DOI: 10.1016/j.aam.2024.102741

The summer holidays are ending, which for many concludes with a long drive home and reliance on GPS devices to get safely home. But every now and then, GPS devices can suggest strange directions or get briefly confused about your location. But until now, no one knew for sure when the satellites were in a good enough position for the GPS system to give reliable direction.

TU/e’s Mireille Boutin and her co-worker Gregor Kemper at the Technical University of Munich have turned to mathematics to help determine when your GPS system has enough information to determine your location accurately. The research is published in the journal Advances in Applied Mathematics.

“In 200 meters, turn right.” This is a typical instruction that many have heard from their global positioning system (GPS).

Without a doubt, advancements in GPS technologies and mobile navigation apps have helped GPS play a major role in modern car journeys.

But, strictly adhering to instructions from GPS devices can lead to undesirable situations. Less serious might be turning left instead of right, while more serious could be driving your car into a harbor—just as two tourists did in Hawaii in 2023. The latter incident is very much an exception to the rule, and one might wonder: “How often does this happen and why?”

GPS and your visibility

“The core of the GPS system was developed in the mid-1960s. At the time, the theory behind it did not provide any guarantee that the location given would be correct,” says Boutin, professor at the Department of Mathematics and Computer Science.

It won’t come as a surprise then to learn that calculating an object’s position on Earth relies on some nifty mathematics. And they haven’t changed much since the early days. These are at the core of the GPS system we all use. And it deserved an update.

So, along with her colleague Gregor Kemper at the Technical University of Munich, Boutin turned to mathematics to expand on the theory behind the GPS system, and their finding has recently been published in the journal Advances in Applied Mathematics.

How does GPS work?

Before revealing Boutin and Kemper’s big finding, just how does GPS work?

Global positioning is all about determining the position of a device on Earth using signals sent by satellites. A signal sent by a satellite carries two key pieces of information—the position of the satellite in space and the time at which the position was sent by the satellite. By the way, the time is recorded by a very precise clock on board the satellite, which is usually an atomic clock.

Thanks to the atomic clock, satellites send very accurate times, but the big issue lies with the accuracy of the clock in the user’s device—whether it’s a GPS navigation device, a smartphone, or a running watch.

“In effect, GPS combines precise and imprecise information to figure out where a device is located,” says Boutin. “GPS might be widely used, but we could not find any theoretical basis to guarantee that the position obtained from the satellite signals is unique and accurate.”

Google says ‘four’

If you do a quick Google search for the minimum number of satellites needed for navigation with GPS, multiple sources report that you need at least four satellites.

But the question is not just how many satellites you can see, but also what arrangements can they form? For some arrangements, determining the user position is impossible. But what arrangements exactly? That’s what the researchers wanted to find out.

“We found conjectures in scientific papers that seem to be widely accepted, but we could not find any rigorous argument to support them anywhere. Therefore, we thought that, as mathematicians, we might be able to fill that knowledge gap,” Boutin says.

To solve the problem, Boutin and Kemper simplified the GPS problem to what works best in practice: equations that are linear in terms of the unknown variables.

“A set of linear equations is the simplest form of equations we could hope for. To be honest, we were surprised that this simple set of linear equations for the GPS problem wasn’t already known,” Boutin adds.

The problem of uniqueness

With their linear equations ready, Boutin and Kemper then looked closely at the solutions to the equations, paying special attention as to whether the equations gave a unique solution.

“A unique solution implies that the only solution to the equations is the actual position of the user,” notes Boutin.

If there is more than one solution to the equations, then only one is correct—that is, the true user position—but the GPS system would not know which one to pick and might return the wrong one.

The researchers found that nonunique solutions can emerge when the satellites lie in a special structure known as a “hyperboloid of revolution of two sheets.”

“It doesn’t matter how many satellites send a signal—if they all lie on one of these hyperboloids then it’s possible that the equations can have two solutions, so the one chosen by the GPS could be wrong,” says Boutin.

But what about the claim that you need at least four satellites to determine your position? “Having four satellites can work, but the solution is not always unique,” points out Boutin.

Why mathematics matters

For Boutin, this work demonstrates the power and application of mathematics.

“I personally love the fact that mathematics is a very powerful tool with lots of practical applications,” says Boutin. “I think people who are not mathematicians may not see the connections so easily, and so it is always nice to find clear and compelling examples of everyday problems where mathematics can make a difference.”

Central to Boutin and Kemper’s research is the field of algebraic geometry in which abstract algebraic methods are used to solve geometrical, real-world problems.

“Algebraic geometry is an area of mathematics that is considered very abstract. I find it nice to be reminded that any piece of mathematics, however abstract it might be, may turn out to have practical applications at some point,” says Boutin.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article to be given Eindhoven University of Technology

Number theoretic transform (NTT) is widely recognized as the most efficient method for computing polynomial multiplication with high dimension and integral coefficients, due to its quasilinear complexity.

What is the relationship between the NTT variants that are constructed by splitting the original polynomials into groups of lower-degree sub-polynomials, such as K-NTT, H-NTT, and G3-NTT? Can they be seen as special cases of a certain algorithm under different parameterizations?

To solve the problems, a research team led by Yunlei Zhao published new research on 15 August 2024 in Frontiers of Computer Science.

The team proposed the first Generalized Splitting-Ring Number Theoretic Transform, referred to as GSR-NTT. Then, they investigated the relationship between K-NTT, H-NTT, and G3-NTT.

In the research, they investigate generalized splitting-ring polynomial multiplication based on the monic incremental polynomial variety, and they propose the first Generalized Splitting-Ring Number Theoretic Transform, referred to as GSR-NTT. They demonstrate that K-NTT, H-NTT, and G3-NTT can be regarded as special cases of GSR-NTT under different parameterizations.

They introduce a succinct methodology for complexity analysis, based on which GSR-NTT can derive its optimal parameter settings. They provide GSR-NTT other instantiations based on cyclic convolution-based polynomials and power-of-three cyclotomic polynomials.

They apply GSR-NTT to accelerate polynomial multiplication in the lattice-based scheme named NTTRU and single polynomial multiplication over power-of-three cyclotomic polynomial rings. The experimental results show that, for NTTRU, GSR-NTT achieves speed-ups of 24.7%, 37.6%, and 28.9% for the key generation, encapsulation, and decapsulation algorithms, respectively, leading to a total speed-up of 29.4%.

Future work can focus on implementing GSR-NTT on more platforms.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article to be given Frontiers Journals

Caption:Part of a new algorithm developed at MIT solves the so-called Fokker-Planck equation, where heat diffuses in a linear way, but there are additional terms that drift in the same direction heat is spreading. In a straightforward application, the approach models how swirls would evolve over the surface of a triangulated sphere. Credit: Alex Shipps / MIT CSAIL and the researchers

Computer graphics and geometry processing research provide the tools needed to simulate physical phenomena like fire and flames, aiding the creation of visual effects in video games and movies as well as the fabrication of complex geometric shapes using tools like 3D printing.

Under the hood, mathematical problems called partial differential equations (PDEs) model these natural processes. Among the many PDEs used in physics and computer graphics, a class called second-order parabolic PDEs explain how phenomena can become smooth over time. The most famous example in this class is the heat equation, which predicts how heat diffuses along a surface or in a volume over time.

Researchers in geometry processing have designed numerous algorithms to solve these problems on curved surfaces, but their methods often apply only to linear problems or to a single PDE. A more general approach by researchers from MIT’s Computer Science and Artificial Intelligence Laboratory (CSAIL) tackles a general class of these potentially nonlinear problems.

In a paper recently published in the ACM Transactions on Graphics journal and presented at the SIGGRAPH conference, they describe an algorithm that solves different nonlinear parabolic PDEs on triangle meshes by splitting them into three simpler equations that can be solved with techniques graphics researchers already have in their software toolkit. This framework can help better analyse shapes and model complex dynamical processes.

“We provide a recipe: If you want to numerically solve a second-order parabolic PDE, you can follow a set of three steps,” says lead author Leticia Mattos Da Silva, an MIT Ph.D. student in electrical engineering and computer science (EECS) and CSAIL affiliate. “For each of the steps in this approach, you’re solving a simpler problem using simpler tools from geometry processing, but at the end, you get a solution to the more challenging second-order parabolic PDE.”

To accomplish this, Mattos Da Silva and her co-authors used Strang splitting, a technique that allows geometry processing researchers to break the PDE down into problems they know how to solve efficiently.

First, their algorithm advances a solution forward in time by solving the heat equation (also called the “diffusion equation”), which models how heat from a source spreads over a shape. Picture using a blow torch to warm up a metal plate—this equation describes how heat from that spot would diffuse over it. This step can be completed easily with linear algebra.

Now, imagine that the parabolic PDE has additional nonlinear behaviours that are not described by the spread of heat. This is where the second step of the algorithm comes in: it accounts for the nonlinear piece by solving a Hamilton-Jacobi (HJ) equation, a first-order nonlinear PDE.

While generic HJ equations can be hard to solve, Mattos Da Silva and co-authors prove that their splitting method applied to many important PDEs yields an HJ equation that can be solved via convex optimization algorithms. Convex optimization is a standard tool for which researchers in geometry processing already have efficient and reliable software. In the final step, the algorithm advances a solution forward in time using the heat equation again to advance the more complex second-order parabolic PDE forward in time.

Among other applications, the framework could help simulate fire and flames more efficiently. “There’s a huge pipeline that creates a video with flames being simulated, but at the heart of it is a PDE solver,” says Mattos Da Silva. For these pipelines, an essential step is solving the G-equation, a nonlinear parabolic PDE that models the front propagation of the flame and can be solved using the researchers’ framework.

The team’s algorithm can also solve the diffusion equation in the logarithmic domain, where it becomes nonlinear. Senior author Justin Solomon, associate professor of EECS and leader of the CSAIL Geometric Data Processing Group, had previously developed a state-of-the-art technique for optimal transport that requires taking the logarithm of the result of heat diffusion.

Mattos Da Silva’s framework provided more reliable computations by doing diffusion directly in the logarithmic domain. This enabled a more stable way, for example, to find a geometric notion of average among distributions on surface meshes like a model of a koala.

Even though their framework focuses on general, nonlinear problems, it can also be used to solve linear PDE. For instance, the method solves the Fokker-Planck equation, where heat diffuses in a linear way, but there are additional terms that drift in the same direction heat is spreading. In a straightforward application, the approach modeled how swirls would evolve over the surface of a triangulated sphere. The result resembles purple-and-brown latte art.

The researchers note that this project is a starting point for tackling the nonlinearity in other PDEs that appear in graphics and geometry processing head-on. For example, they focused on static surfaces but would like to apply their work to moving ones, too. Moreover, their framework solves problems involving a single parabolic PDE, but the team would also like to tackle problems involving coupled parabolic PDE. These types of problems arise in biology and chemistry, where the equation describing the evolution of each agent in a mixture, for example, is linked to the others’ equations.

Mattos Da Silva and Solomon wrote the paper with Oded Stein, assistant professor at the University of Southern California’s Viterbi School of Engineering.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article to be given Alex Shipps, Massachusetts Institute of Technology

An upside-down sea ice slab showcasing brine channels that facilitate the drainage of liquid brine and support convection along the interface.

A new applied mathematical theory could enhance our understanding of how sea ice affects global climate, potentially improving the accuracy of climate predictions.

The authors of a new paper published in the Proceedings of the Royal Society A: Mathematical and Physical Sciences, offer new insights into how heat travels through sea ice, a crucial factor in regulating Earth’s polar climate.

Dr. Noa Kraitzman, Senior Lecturer in Applied Mathematics at Macquarie University and lead author of the study, says the research addresses a key gap in current climate modeling.

“Sea ice covers about 15% of the ocean’s surface during the coldest season when it’s at its vast majority,” Dr. Kraitzman says. “It’s a thin layer that separates the atmosphere and the ocean and is responsible for heat transfer between the two.”

Sea ice acts as an insulating blanket on the ocean, reflecting sunlight and moderating heat exchange. As global temperatures rise, understanding how sea ice behaves will become increasingly important for predicting climate change.

The study focuses on the thermal conductivity of sea ice, a critical parameter used in many global climate models. The movement of liquid brine within sea ice, which can potentially increase its heat transport, was not accounted for in previous models.

Dr. Kraitzman says the unique structure of sea ice, along with its sensitive dependence on temperature and salinity, means it is challenging to measure and predict its properties, specifically its thermal conductivity.

“When you look at sea ice on a small scale, what makes it interesting is its complex structure because it’s made up of ice, air bubbles, and brine inclusions.

“As the atmosphere above the ocean becomes extremely cold, below minus 30 degrees Celsius, while the ocean water remains at about minus two degrees, this creates a large temperature difference, and the water freezes from the top down.

“As the water freezes rapidly, it pushes out the salt, creating an ice matrix of purely frozen water which captures air bubbles and pockets of very salty water, called brine inclusions, surrounded by nearly pure ice.”

These dense brine inclusions are heavier than the fresh ocean water which results in convective flow within the ice, creating big “chimneys” where liquid salt flows out.

The research builds on earlier field work by Trodahl in 1999, which first suggested that fluid flow within sea ice might enhance its thermal conductivity. Dr. Kraitzman’s team has now provided mathematical proof of this phenomenon.

“Our mathematics definitely shows that such an enhancement should be expected once convective flow within the sea ice begins,” Dr. Kraitzman says.

The model also offers a way to relate the sea ice’s thermal properties to its temperature and salt content, allowing theoretical results to be compared with measurements.Specifically, it provides a tool to be used in large-scale climate models, potentially leading to more accurate predictions of future conditions in the polar regions. Sea ice in the Arctic has been declining rapidly in recent decades. This loss of ice can lead to a feedback loop: as more dark ocean water is exposed, it absorbs more sunlight, leading to further warming and ice loss.The loss of sea ice can affect weather patterns, ocean circulation, and marine ecosystems far beyond the polar regions.

Dr. Kraitzman says understanding the thermal conductivity of sea ice is important for predicting its future.

The researchers note that while their model provides a theoretical framework, more experimental work is needed to integrate these findings into large-scale climate models. The study was conducted by mathematicians from Macquarie University in Australia, the University of Utah and Dartmouth College, New Hampshire in the U.S.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article to be given Macquarie University

The ouzo phase diagram. The full figure legend can be found in the corresponding journal paper.

Mathematicians at Loughborough University have turned their attention to a fascinating observation that has intrigued scientists and cocktail enthusiasts alike: the mysterious way ouzo, a popular anise-flavored liquor, turns cloudy when water is added.

The researchers’ exploration of this seemingly simple phenomenon, known as the “Ouzo Effect,” has resulted in a new mathematical model that offers insights into the spontaneous formation of microscopic droplets and how they can remain suspended in a liquid for a long time.

Revealing the math taking place in the glass could have far-reaching implications beyond the world of beverages, such as the creation of new materials.

“Ouzo is essentially three things: alcohol, anise oil, and water,” explains Dr. David Sibley, an expert in mathematical modeling.

“When water is added, microscopic droplets form that are made mostly of oil, and these are a result of the anise oil separating from the alcohol-water mixture. This causes the drink to turn cloudy as the droplets scatter light.”

He continued, “This emulsification—the suspension of well-mixed oil droplets in the liquid—is something that requires a lot of energy in other systems and foods. For example, food emulsions such as mayonnaise and salad dressings require vigorous whisking to achieve a smooth and stable mixture. For ouzo, however, the emulsification happens spontaneously.

“What’s also surprising is how long these droplets, and the resulting cloudiness, remain stable in the mixture without separating, especially when compared to other food emulsions. If you’ve ever made an olive oil and balsamic vinegar dressing, you’ll notice that the two liquids start to separate after a short time, requiring more whisking to bring them back together. The ouzo-water emulsion remains stable for a much longer period.

“Understanding how and why this happens in ouzo could lead to the development of new materials, especially in fields such as in pharmaceuticals, cosmetics, and food products, where the stability and distribution of microscopic particles are critical.”

The Loughborough researchers, in collaboration with experts from the University of Edinburgh and Nottingham Trent University, have uncovered the mathematical principles that explain how the droplets and surrounding liquid—two distinct ‘phases’ within the mixture—form and can remain stable together for long periods.

By mixing alcohol, oil, and water in varying proportions, they were able to observe phase separation and measure key properties like surface tension.

They used this data and a statistical mechanical modeling method known as ‘classical density functional theory’ to develop their mathematical model.

This model has been used to calculate a phase diagram that details the stable combinations of the ouzo ingredients.

The research has been published in the journal Soft Matter and is featured on the front cover of the latest issue. The paper is titled “Experimental and theoretical bulk phase diagram and interfacial tension of ouzo.”

“You could say, what looks cloudy is now clearer,” said Professor Andrew Archer, the first author of the journal paper.

“What is also fun is that simple models like this can predict a lot—similar to recent, parallel research we did that reveals how long droplets we sneeze into the air can persist.

“As is often the case, ‘blue skies’ fundamental research can say something profound about an experience that occurs in regular life—like serving and drinking ouzo.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article to be given  Meg Cox, Loughborough University

Sequences of consecutive breakpoint distances for “Gates of Paradise” and “Finnegans Wake” in the same scale. Credit: Stanisław Drożdż

Statistical analysis of classic literature has shown that the way punctuation breaks up text obeys certain universal mathematical relationships. James Joyce’s tome “Finnegans Wake,” however, famously breaks the rules of normal prose through its unusual, dreamlike stream of consciousness. New work in chaos theory, published in the journal Chaos, takes a closer look at how Joyce’s challenging novel stands out, mathematically.

Researchers have compared the distribution of punctuation marks in various experimental novels to determine the underlying order of “Finnegans Wake.” By statistically analysing the texts, the team has found that the tome exhibits an unusual but statistically identifiable structure.

“‘Finnegans Wake’ exhibits the type of narrative that makes it possible to continue longer strings of words without the need for punctuation breaks,” said author Stanisław Drożdż. “This may indicate that this type of narrative is less taxing on the human perceptual and respiratory systems or, equivalently, that it resonates better with them.”

As word sequences run longer without punctuation marks, the higher the probability that a punctuation mark appears next. Such a relationship is called a Weibull distribution. Weibull distributions apply to anything from human diseases to “The Gates of Paradise,” a Polish novel written almost entirely in a single sentence spanning nearly 40,000 words.

Enter “Finnegans Wake,” which weaves together puns, phrases, and portmanteaus from up to 70 languages into a dreamlike stream of consciousness. The book typifies Joyce’s later works, some of the only known examples to appear to not adhere to the Weibull distribution in punctuation.

The team broke down 10 experimental novels by word counts between punctuation marks. These sets of numbers were compiled into a singularity spectrum for each book that described how orderly sentences of different lengths are proportioned. “Finnegans Wake” has a notoriously broad range of sentence lengths, making for a wide spectrum.

While most punctuation distributions skew toward shorter word sequences, the wide singularity spectrum in “Finnegans Wake” was perfectly symmetrical, meaning sentence length variability follows an orderly curve.

This level of symmetry is a rare feat in the real world, implying a well-organized, complex hierarchical structure that aligns perfectly with a phenomenon known as multifractality, systems represented by fractals within fractals.

“‘Finnegans Wake’ appears to have the unique property that the probability of interrupting a sequence of words with a punctuation character decreases with the length of the sequence,” Drożdż said. “This makes the narrative more flexible to create perfect, long-range correlated cascading patterns that better reflect the functioning of nature.”

Drożdż hopes the work helps large language models better capture long-range correlations in text. The team next looks to apply their work in this domain.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article to be given   American Institute of Physics

For the first time, a speedcuber has demonstrated a solution to the Rubik’s cube that combines the two final steps of the puzzle’s solution into one.

A Rubik’s cube solver has become the first person to show proof of successfully combining the final two steps of solving the mechanical puzzle into one move. The feat required the memorisation of thousands of possible sequences for the final step.

Most skilled speedcubers – people who compete to solve Rubik’s cubes with the most speed and efficiency – choose to solve the final layer of the cube with two separate moves that involve 57 possible sequences for the penultimate step and 21 possible sequences for the final move.

Combining those two separate actions into a single move requires a person to memorise 3915 possible sequences. These sequences were previously known to be possible, but nobody is reported to have successfully achieved this so-called “Full 1 Look Last Layer” (Full 1LLL) move until a speedcuber going by the online username “edmarter” shared a YouTube video demonstrating that accomplishment.

Edmarter says he decided to take up the challenge after seeing notable speedcubers try and fail. Over the course of about a year, he spent 10 hours each weekend and any free time during the week practising and memorising the necessary sequences, he told New Scientist. That often involved memorising 144 movement sequences in a single day.

All that effort paid off on 4 August 2022 when edmarter uploaded a video demonstrating the Full 1LLL over the course of 100 separate puzzle solves. He also posted his accomplishment to Reddit’s r/Cubers community.

His average solve time for each Rubik’s cube over the course of that video demonstration run was 14.79 seconds. He says he had an average solve time as low as 12.50 seconds during two practice runs before recording the video.

The Rubik’s cube community has reacted with overwhelming enthusiasm and awe. The top-voted comment on his Reddit post detailing the achievement simply reads: “This is absolutely insane.”

But he is not resting on his laurels. Next up, he plans to try practising some other methods for finishing the Rubik’s cube that have only previously been mastered by a handful of people.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Jeremy Hsu*