Month: July 2024

左側的 14 邊形 Tile(1,1) 被稱為弱手性非週期單瓦 — 換句話說，如果禁止混合未反射和反射瓦片的鋪砌，則它僅以非週期性方式鋪砌。 然而，透過修改其邊緣，如中心和右側所示，可以創建稱為「幽靈」的嚴格手性非週期單瓦，這些單瓦僅允許非週期性鋪砌。 圖片來源：滑鐵盧大學

最近，一個由四人組成的國際團隊（包括 Cheriton 電腦科學學院教授 Craig Kaplan 博士）發現了一種單一形狀，可以鋪滿平面（一個無限的二維表面），其圖案永遠無法重複。

這一發現讓數學家、鋪砌愛好者和公眾都為之著迷。

這種形狀，一個 13 邊形，他們稱之為「帽子」，數學家稱之為非週期單瓦或「愛因斯坦」，這個德語詞的意思是「一塊石頭」。

但該團隊最近的發現再次提高了標準。 他們發現了另一種與第一種形狀相關的形狀，它符合更嚴格的定義。 這種被稱為「幽靈」的新形狀，以一種永遠不會重複的模式鋪滿平面，而無需使用該形狀的鏡像。 因此，它也被稱為「吸血鬼愛因斯坦」— 一種無需反射即可非週期性鋪砌的形狀。

「我們的第一篇論文解決了愛因斯坦問題，但由於該形狀需要反射才能進行非週期性鋪砌，因此人們提出了一個合理的問題：是否有一種形狀可以像帽子一樣，但無需反射，」Kaplan 解釋說。 「我們很幸運地找到了一種形狀，它不僅解決了這個子問題，而且在第一篇論文發表後不久就解決了它。」

對於數學家來說，帽子及其鏡像是一個單一的形狀，但在物理世界中，左手和右手的形狀表現可能不同。 例如，你不能在左手上戴右手手套。

「如果你用帽子形狀的瓷磚以非週期性方式鋪砌一個大型浴室地板，這些瓷磚的一面已經上釉，那麼你需要帽子和帽子的鏡像，」Kaplan 說。

但並非這種吹毛求疵促成了最近的發現。

吸血鬼愛因斯坦的發現始於 David Smith 的沉思，他是一位退休的印刷技術員，也是一位來自英國約克郡的自稱形狀愛好者，幾個月前他的好奇心促成了最初的愛因斯坦發現。

「在我們的帽子論文上線幾天后，Dave 給我們發了一封電子郵件，說他一直在玩一種相關的形狀，這種形狀的表現似乎很奇怪，」Kaplan 說。 「日本數學家兼著名藝術家 Yoshiaki Araki 的作品具有 MC Escher 的精神，他發布了 Tile(1,1) 的圖片，這引起了 Dave 的興趣，並進一步研究它。」

Yoshiaki 在 Twitter 上發布了一個有趣的問題：「基於新的非週期單瓦 Tile(1, 1.1) 的非週期海龜鑲嵌。在鑲嵌中，據說大約 12.7% 的瓷磚被反射。綠色的是一個例子。在鑲嵌中還隱藏著另一隻被反射的海龜。誰是被反射的？」

「Yoshi 將 Tile(1,1) 變成了海龜，很難在圖片中看到另一隻被反射的海龜。但這引起了 Dave 的好奇。如果我們用這種形狀鋪砌，但不進行反射呢？當他這樣做時，Dave 發現他可以逐步向外構建鋪砌，其模式不會停止也不會重複。」

但這種形狀帶有不同的吹毛求疵。 正如 Kaplan 解釋的那樣，如果你使用 Tile(1,1) 的反射，則圖案會重複。 換句話說，它是週期性的。 但是，如果通過用曲線替換其直線邊緣來修改 Tile(1,1)，它就會變成吸血鬼愛因斯坦 — 一種單一形狀，無需反射即可在永不重複的模式中鋪砌無限平面。

對於數學家和鋪砌愛好者來說，顯而易見的問題是下一步是什麼？

「我們可以提出這個問題的許多變體，」Kaplan 說。 「至少對我來說，最有趣的是這是否可以在 3D 中完成。如果有一種形狀可以在三個維度中非週期性地重複，那就太好了。這樣的結構很難視覺化，但如果我們有幸找到一種三維形狀（一種多形體），像帽子一樣僅以非週期性方式鋪砌，那麼在計算上證明它並不會困難得多。」

「作為數學的一個分支，鋪砌理論是美麗的、有形的，並且有很多有趣的問題需要解決。不乏後續工作要做。」

Hatfest，一個慶祝「帽子」發現的活動，將於 7 月 20 日至 21 日在牛津大學數學研究所舉行。 該活動的第一天將以針對普通觀眾的關於鋪砌的講座和研討會為特色，而第二天將以針對廣泛的物理學家和數學家觀眾的演示為特色。

如需更多此類見解，請登入我們的網站 https://international-maths-challenge.com

本文的作者為滑鐵盧大學的 Joe Petrik

المضلع ذو الـ14 ضلعاً Tile(1,1)، على اليسار، معروف بأنه بلاطة أحادية لا دورية ضعيفة التماثل – بمعنى آخر، إذا كانت التبليطات التي تمزج بين البلاطات غير المنعكسة والمنعكسة محظورة، فإنها تبلط فقط بشكل لا دوري. ومع ذلك، من خلال تعديل حوافها، كما هو موضح في الوسط واليمين، تم إنشاء بلاطات أحادية لا دورية صارمة التماثل تسمى ””أطياف”“ لا تسمح إلا بتبليطات غير دورية. المصدر: جامعة واترلو

اكتشف مؤخراً فريق دولي مكون من أربعة أشخاص، من بينهم الدكتور كريج كابلان أستاذ مدرسة تشيريتون لعلوم الحاسوب، شكلاً واحداً يبلط المستوى – وهو سطح ثنائي الأبعاد لا نهائي – في نمط لا يمكن أبداً جعله يتكرر.

أذهل هذا الاكتشاف علماء الرياضيات وهواة التبليط والجمهور على حد سواء.

الشكل، وهو مضلع ذو 13 ضلعاً أطلقوا عليه اسم ””القبعة”“، معروف لدى علماء الرياضيات باسم البلاطة الأحادية اللادورية أو ””آينشتاين”“، وهي كلمة ألمانية تعني ””حجر واحد”“.

لكن اكتشاف الفريق الأخير رفع المستوى مرة أخرى. لقد وجدوا شكلاً آخر، مرتبطاً بالأول، يلبي تعريفاً أكثر صرامة. أُطلق على الشكل الجديد اسم ””الطيف”“، وهو يبلط المستوى في نمط لا يتكرر أبداً دون استخدام صور مرآوية للشكل. لهذا السبب، أُطلق عليه أيضاً اسم ””آينشتاين مصاص الدماء”“ – وهو شكل يبلط بشكل لا دوري دون الحاجة إلى انعكاسه.

””حلت ورقتنا الأولى مشكلة آينشتاين، ولكن نظراً لأن الشكل يتطلب انعكاساً للتبليط بشكل لا دوري، طرح الناس سؤالاً مشروعاً: هل هناك شكل يمكنه فعل ما تفعله القبعة ولكن بدون انعكاس،”“ يشرح كابلان. ””كان من حسن حظنا أننا وجدنا شكلاً لا يحل هذه المشكلة الفرعية فحسب، بل حلها أيضاً بعد وقت قصير من نشر الورقة الأولى.”“

بالنسبة لعلماء الرياضيات، تعتبر القبعة وصورتها المرآوية شكلاً واحداً، ولكن في العالم المادي يمكن أن تتصرف الأشكال اليسرى واليمنى بشكل مختلف. لا يمكنك، على سبيل المثال، ارتداء قفاز أيمن على يدك اليسرى.

””إذا قمت بتبليط أرضية حمام كبيرة بشكل لا دوري باستخدام بلاط على شكل قبعة تم تزجيجه من جانب واحد، فستحتاج إلى قبعات وصور مرآوية للقبعات،”“ يقول كابلان.

لكن لم يكن هذا الجدل هو الذي حفز الاكتشاف الأخير.

بدأ اكتشاف آينشتاين مصاص الدماء بتأملات ديفيد سميث، وهو فني طباعة متقاعد وهاوي أشكال كما يصف نفسه من يوركشاير، إنجلترا، الذي أدى فضوله قبل أشهر إلى اكتشاف آينشتاين الأصلي.

””أرسل ديف لنا بريداً إلكترونياً بعد يومين من نشر ورقة القبعة عبر الإنترنت ليقول إنه كان يعبث بشكل مرتبط بها وبدا أنه يتصرف بشكل غريب،”“ يقول كابلان. ””يوشياكي أراكي، وهو عالم رياضيات ياباني وفنان معروف يعمل بروح إم سي إيشر، نشر صوراً لـ Tile(1,1) جعلت ديف مهتماً بالنظر إليها بشكل أعمق.”“

نشر يوشياكي سؤالاً مثيراً للاهتمام على تويتر: “تبليط سلحفاة لا دوري مبني على بلاطة أحادية لا دورية جديدة Tile(1, 1.1). في التبليط، يُقال إن حوالي 12.7% من البلاطات منعكسة. اللون الأخضر هو مثال. هناك سلحفاة منعكسة أخرى مخفية في التبليط. من هي المنعكسة؟'”

””حوّل يوشي Tile(1,1) إلى سلاحف ومن الصعب بعض الشيء رؤية السلحفاة المنعكسة الأخرى في تلك الصورة. لكن هذا أثار فضول ديف. ماذا لو قمنا بالتبليط بهذا الشكل ولكن بدون انعكاسات؟ وبينما كان يفعل ذلك، وجد ديف أنه يمكنه بناء تبليطات تتوسع تدريجياً للخارج في نمط لا يتوقف ولا يتكرر.”“

لكن هذا الشكل جاء مع جدل مختلف. كما يشرح كابلان، إذا استخدمت انعكاسات Tile(1,1) فإن النمط يتكرر. بمعنى آخر، إنه دوري. ولكن إذا تم تعديل Tile(1,1) عن طريق استبدال حوافه المستقيمة بمنحنيات، فإنه يصبح آينشتاين مصاص دماء – شكل واحد بدون انعكاس يبلط المستوى اللانهائي في نمط لا يمكن أبداً جعله يتكرر.

السؤال الواضح لعلماء الرياضيات وهواة التبليط هو ما الخطوة التالية؟

””يمكننا طرح العديد من الاختلافات للمشكلة،”“ يقول كابلان. ””الأكثر إثارة للاهتمام، بالنسبة لي على الأقل، هو ما إذا كان يمكن القيام بذلك في الأبعاد الثلاثية. سيكون من الجميل أن يكون لدينا شكل يتكرر بشكل غير دوري في ثلاثة أبعاد. مثل هذه التركيبات أصعب بكثير في التصور، ولكن من الناحية الحسابية ليس من الصعب إثباتها إذا كنا محظوظين بما يكفي للعثور على شكل ثلاثي الأبعاد – متعدد الأشكال – الذي مثل القبعة يبلط فقط بشكل لا دوري.”“

””نظرية التبليط كفرع من الرياضيات جميلة وملموسة وتحتوي على الكثير من المشاكل المثيرة للاهتمام التي يجب حلها. لا يوجد نقص في العمل المتابع الذي يجب القيام به.”“

سيقام مهرجان القبعة، احتفالاً باكتشاف ””القبعة”“، في معهد الرياضيات بجامعة أكسفورد من 20 إلى 21 يوليو. سيتضمن اليوم الأول من الحدث محادثات وورش عمل حول التبليط موجهة للجمهور العام، بينما سيتضمن اليوم الثاني عروضاً تقديمية موجهة لجمهور واسع من الفيزيائيين وعلماء الرياضيات.

لمزيد من هذه الرؤى، قم بتسجيل الدخول إلى موقعنا https://international-maths-challenge.com

تُنسب المقالة إلى جو بيتريك، جامعة واترلو

Le polygone à 14 côtés Tile(1,1), à gauche, est connu comme un monotuile apériodique faiblement chiral — en d’autres termes, si les pavages qui mélangent des tuiles non réfléchies et réfléchies sont interdits, alors il ne pave que de manière apériodique. Cependant, en modifiant ses bords, comme montré au centre et à droite, des monotuiles apériodiques strictement chiraux appelés « spectres » sont créés qui n’admettent que des pavages non périodiques. Crédit : Université de Waterloo

Récemment, une équipe internationale de quatre personnes, qui inclut le professeur Dr. Craig Kaplan de l’École d’informatique Cheriton, a découvert une forme unique qui pave le plan — une surface infinie bidimensionnelle — selon un motif qui ne peut jamais être rendu répétitif.

La découverte a fasciné les mathématiciens, les passionnés de pavage et le grand public.

La forme, un polygone à 13 côtés qu’ils ont appelé « le chapeau », est connue des mathématiciens comme un monotuile apériodique ou un « einstein », les mots allemands qui signifient « une pierre ».

Mais la découverte la plus récente de l’équipe a encore relevé la barre. Ils ont trouvé une autre forme, liée à la première, qui répond à une définition encore plus stricte. Surnommée le « spectre », la nouvelle forme pave un plan selon un motif qui ne se répète jamais sans utiliser d’images miroir de la forme. Pour cette raison, elle a aussi été appelée un « einstein vampire » — une forme qui pave de manière apériodique sans nécessiter sa réflexion.

« Notre premier article a résolu le problème d’einstein, mais comme la forme nécessitait une réflexion pour paver de manière apériodique, les gens ont soulevé une question légitime : Existe-t-il une forme qui peut faire ce que fait le chapeau mais sans réflexion », explique Kaplan. « Nous avons eu la chance de trouver une forme qui non seulement résout ce sous-problème, mais l’a aussi résolu si peu de temps après le premier article. »

Pour les mathématiciens, le chapeau et son image miroir constituent une seule forme, mais dans le monde physique, les formes gauches et droites peuvent se comporter différemment. Vous ne pouvez pas, par exemple, porter un gant de la main droite sur votre main gauche.

« Si vous paviez le sol d’une grande salle de bain de manière apériodique avec des tuiles en forme de chapeau qui auraient été émaillées d’un côté, vous auriez besoin de chapeaux et d’images miroir de chapeaux », dit Kaplan.

Mais ce n’est pas cette chicane qui a motivé la découverte récente.

La découverte de l’einstein vampire a commencé avec les réflexions de David Smith, un technicien d’imprimerie retraité et passionné de formes autodidacte du Yorkshire, en Angleterre, dont la curiosité quelques mois plus tôt avait mené à la découverte originale d’einstein.

« Dave nous a envoyé un courriel quelques jours après que notre article sur le chapeau soit mis en ligne pour dire qu’il avait joué avec une forme apparentée qui semblait se comporter étrangement », dit Kaplan. « Yoshiaki Araki, un mathématicien japonais et artiste bien connu dont le travail est dans l’esprit de MC Escher, avait publié des images de Tile(1,1) qui ont intéressé Dave à l’examiner davantage. »

Yoshiaki a posté une question intrigante sur Twitter : « Une tessellation de tortue apériodique basée sur le nouveau monotuile apériodique Tile(1, 1.1). Dans le pavage, il est dit qu’environ 12,7 % des tuiles sont réfléchies. La verte en est un exemple. Une tortue réfléchie de plus est cachée dans le pavage. Qui est la réfléchie ? »

« Yoshi avait transformé Tile(1,1) en tortues et il est un peu difficile de voir l’autre tortue réfléchie dans cette image. Mais cela a rendu Dave curieux. Et si nous pavions avec cette forme mais sans réflexions ? En faisant cela, Dave a trouvé qu’il pouvait construire des pavages progressivement vers l’extérieur selon un motif qui ne s’arrêtait pas et ne se répétait pas. »

Mais alors cette forme est venue avec une chicane différente. Comme l’explique Kaplan, si vous utilisez des réflexions de Tile(1,1), le motif se répète effectivement. En d’autres termes, il est périodique. Mais si Tile(1,1) est modifié en remplaçant ses bords droits par des courbes, il devient un einstein vampire — une forme unique qui sans réflexion pave le plan infini selon un motif qui ne peut jamais être rendu répétitif.

La question évidente pour les mathématiciens et les passionnés de pavage est : quelle est la suite ?

« Nous pouvons poser de nombreuses variations du problème », dit Kaplan. « La plus intéressante, pour moi du moins, est de savoir si cela peut être fait en 3D. Il serait agréable d’avoir une forme qui se répète de manière non périodique en trois dimensions. De telles constructions sont beaucoup plus difficiles à visualiser, mais informatiquement ce n’est pas tellement plus difficile à prouver si nous avons la chance de trouver une forme tridimensionnelle — une polyforme — qui comme le chapeau ne pave que de manière apériodique. »

« La théorie du pavage en tant que branche des mathématiques est belle, tangible, et a beaucoup de problèmes fascinants à résoudre. Il n’y a pas de pénurie de travaux de suivi à faire. »

Hatfest, une célébration de la découverte du « Chapeau », aura lieu à l’Institut mathématique de l’Université d’Oxford du 20 au 21 juillet. Le premier jour de l’événement présentera des conférences et des ateliers sur le pavage destinés à un public profane, tandis que le second présentera des présentations destinées à un large public de physiciens et de mathématiciens.

Pour plus de telles perspectives, connectez-vous à notre site web https://international-maths-challenge.com

Crédit de l’article donné à Joe Petrik, Université de Waterloo

Das 14-seitige Polygon Tile(1,1) links ist als schwach chirale aperiodische Monokachel bekannt – das heißt, wenn Parkettierungen, die ungespiegelte und gespiegelte Kacheln mischen, verboten sind, dann parkettiert es nur aperiodisch. Durch Modifizierung seiner Kanten, wie in der Mitte und rechts gezeigt, werden jedoch streng chirale aperiodische Monokacheln namens „Spectres“ erzeugt, die nur nicht-periodische Parkettierungen zulassen. Quelle: University of Waterloo

Kürzlich entdeckte ein internationales Viererteam, dem Professor Dr. Craig Kaplan von der Cheriton School of Computer Science angehört, eine einzelne Form, die die Ebene – eine unendliche, zweidimensionale Oberfläche – in einem Muster parkettiert, das sich niemals wiederholen lässt.

Die Entdeckung faszinierte Mathematiker, Parkettierungs-Enthusiasten und die Öffentlichkeit gleichermaßen.

Die Form, ein 13-seitiges Polygon, das sie „den Hut“ nannten, ist Mathematikern als aperiodische Monokachel oder als „Einstein“ bekannt, die deutschen Wörter, die „ein Stein“ bedeuten.

Doch die jüngste Entdeckung des Teams hat die Messlatte erneut höher gelegt. Sie fanden eine weitere Form, die mit der ersten verwandt ist und eine noch strengere Definition erfüllt. Die neue Form, die den Namen „Specter“ erhielt, parkettiert eine Ebene in einem Muster, das sich niemals wiederholt, ohne die Verwendung von Spiegelbildern der Form. Aus diesem Grund wurde sie auch als „Vampir-Einstein“ bezeichnet – eine Form, die aperiodisch parkettiert, ohne ihre Spiegelung zu benötigen.

„„Unser erstes Paper löste das Einstein-Problem, aber da die Form eine Spiegelung benötigte, um aperiodisch zu parkettieren, stellten die Leute eine berechtigte Frage: Gibt es eine Form, die das kann, was der Hut kann, aber ohne Spiegelung?“ erklärt Kaplan. „„Es war unser Glück, dass wir eine Form fanden, die nicht nur dieses Teilproblem löst, sondern es auch so kurz nach dem ersten Paper gelöst hat.“

Für Mathematiker sind der Hut und sein Spiegelbild eine einzige Form, aber in der physischen Welt können sich linkshändige und rechtshändige Formen unterschiedlich verhalten. Man kann zum Beispiel keinen rechtshändigen Handschuh an der linken Hand tragen.

„„Wenn man einen großen Badezimmerboden aperiodisch mit hut-förmigen Kacheln parkettieren würde, die auf einer Seite glasiert waren, bräuchte man Hüte und Spiegelbilder von Hüten,“ sagt Kaplan.

Doch es war nicht dieser Einwand, der die jüngste Entdeckung motivierte.

Die Entdeckung des Vampir-Einsteins begann mit den Überlegungen von David Smith, einem pensionierten Drucktechniker und selbsternannten Formen-Liebhaber aus Yorkshire, England, dessen Neugier Monate zuvor zur ursprünglichen Einstein-Entdeckung geführt hatte.

„„Dave mailte uns ein paar Tage, nachdem unser Hut-Paper online gegangen war, um zu sagen, dass er mit einer verwandten Form herumgespielt hatte, die sich seltsam zu verhalten schien,“ sagt Kaplan. „„Yoshiaki Araki, ein japanischer Mathematiker und bekannter Künstler, dessen Werk im Geiste von MC Escher steht, hatte Bilder von Tile(1,1) gepostet, die Dave dazu brachten, sich näher damit zu beschäftigen.“

Yoshiaki stellte eine faszinierende Frage auf Twitter: „Eine aperiodische Schildkröten-Tessellation basierend auf der neuen aperiodischen Monokachel Tile(1, 1.1). In der Parkettierung heißt es, dass etwa 12,7 % der Kacheln gespiegelt sind. Die grüne ist ein Beispiel. Eine weitere gespiegelte Schildkröte ist in der Parkettierung versteckt. Wer ist die gespiegelte?“

„„Yoshi hatte Tile(1,1) in Schildkröten verwandelt, und es ist etwas schwer, die andere gespiegelte Schildkröte auf diesem Bild zu sehen. Aber es machte Dave neugierig. Was wäre, wenn wir mit dieser Form parkettieren, aber ohne Spiegelungen? Als er das tat, stellte Dave fest, dass er Parkettierungen schrittweise nach außen in einem Muster aufbauen konnte, das nicht aufhörte und sich nicht wiederholte.“

Doch dann kam diese Form mit einem anderen Einwand. Wie Kaplan erklärt, wiederholt sich das Muster, wenn man Spiegelungen von Tile(1,1) verwendet. Mit anderen Worten, es ist periodisch. Doch wenn Tile(1,1) modifiziert wird, indem seine geraden Kanten durch Kurven ersetzt werden, wird es zu einem Vampir-Einstein – einer einzelnen Form, die ohne Spiegelung die unendliche Ebene in einem Muster parkettiert, das sich niemals wiederholen lässt.

Die offensichtliche Frage für Mathematiker und Parkettierungs-Enthusiasten ist: Was kommt als Nächstes?

„„Wir können viele Variationen des Problems stellen,“ sagt Kaplan. „„Das Interessanteste, zumindest für mich, ist, ob dies in 3D möglich ist. Es wäre schön, eine Form zu haben, die sich in drei Dimensionen nicht-periodisch wiederholt. Solche Konstruktionen sind viel schwieriger zu visualisieren, aber rechnerisch ist es nicht viel schwieriger zu beweisen, sollten wir das Glück haben, eine dreidimensionale Form – ein Polyform – zu finden, die wie der Hut nur aperiodisch parkettiert.“

„„Die Parkettierungstheorie als Zweig der Mathematik ist schön, greifbar und hat viele faszinierende Probleme zu lösen. Es gibt keinen Mangel an weiterer Arbeit zu tun.“

Hatfest, eine Feier der Entdeckung von „dem Hut,“ findet vom 20. bis 21. Juli am Mathematischen Institut der Universität Oxford statt. Der erste Tag der Veranstaltung bietet Vorträge und Workshops zum Thema Parkettierung, die sich an ein Laienpublikum richten, während der zweite Tag Präsentationen für ein breites Publikum von Physikern und Mathematikern bietet.

Für weitere Einblicke dieser Art besuchen Sie unsere Website https://international-maths-challenge.com

Artikel von Joe Petrik, University of Waterloo

El polígono de 14 lados Tile(1,1), a la izquierda, se conoce como un monotile aperiódico débilmente quiral; en otras palabras, si se prohíben los mosaicos que mezclan tiles no reflejados y reflejados, entonces solo cubre de forma aperiódica. Sin embargo, al modificar sus bordes, como se muestra en el centro y a la derecha, se crean monotiles aperiódicos estrictamente quirales llamados “espectros” que admiten solo mosaicos no periódicos. Crédito: Universidad de Waterloo

Recientemente, un equipo internacional de cuatro personas, que incluye al profesor de la Escuela de Ciencias de la Computación de Cheriton, el Dr. Craig Kaplan, descubrió una forma única que cubre el plano (una superficie bidimensional infinita) en un patrón que nunca se puede hacer que se repita.

El descubrimiento cautivó a matemáticos, entusiastas de los mosaicos y al público por igual.

La forma, un polígono de 13 lados que llamaron “el sombrero”, es conocida por los matemáticos como un monotile aperiódico o un “einstein”, las palabras alemanas que significan “una piedra”.

Pero el descubrimiento más reciente del equipo ha subido el listón una vez más. Encontraron otra forma, relacionada con la primera, que cumple una definición aún más estricta. Apodada el “espectro”, la nueva forma cubre un plano en un patrón que nunca se repite sin el uso de imágenes especulares de la forma. Por esta razón, también se le ha llamado “einstein vampiro”: una forma que cubre aperiódicamente sin necesidad de su reflejo.

“Nuestro primer artículo resolvió el problema de einstein, pero como la forma requería reflexión para cubrir aperiódicamente, la gente planteó una pregunta legítima: ¿Existe una forma que pueda hacer lo que hace el sombrero pero sin reflexión?”, explica Kaplan. “Fue nuestra buena fortuna que encontramos una forma que no solo resuelve este subproblema, sino que también lo resolvió tan pronto después del primer artículo.”

Para los matemáticos, el sombrero y su imagen especular son una sola forma, pero en el mundo físico las formas zurdas y diestras pueden comportarse de manera diferente. No puedes, por ejemplo, usar un guante diestro en tu mano izquierda.

“Si cubrieras un gran suelo de baño aperiódicamente con tiles en forma de sombrero que hubieran sido esmaltados en un lado, necesitarías sombreros e imágenes especulares de sombreros”, dice Kaplan.

Pero no fue esta objeción lo que motivó el reciente descubrimiento.

El descubrimiento del einstein vampiro comenzó con las reflexiones de David Smith, un técnico de impresión jubilado y autodenominado aficionado a las formas de Yorkshire, Inglaterra, cuya curiosidad meses antes condujo al descubrimiento original de einstein.

“Dave nos envió un correo electrónico un par de días después de que nuestro artículo sobre el sombrero se publicara en línea para decir que había estado jugando con una forma relacionada que parecía comportarse de manera extraña”, dice Kaplan. “Yoshiaki Araki, un matemático japonés y artista conocido cuyo trabajo está en el espíritu de MC Escher, había publicado imágenes de Tile(1,1) que hicieron que Dave se interesara en mirarlo más a fondo.”

Yoshiaki publicó una pregunta intrigante en Twitter: “Una teselación de tortugas aperiódicas basada en el nuevo monotile aperiódico Tile(1, 1.1). En la teselación, se dice que alrededor del 12,7% de los tiles se reflejan. El verde es una instancia. Una tortuga más reflejada está oculta en la teselación. ¿Quién es el reflejado?'”

“Yoshi había convertido Tile(1,1) en tortugas y es un poco difícil ver la otra tortuga reflejada en esa imagen. Pero despertó la curiosidad de Dave. ¿Qué pasa si cubrimos con esta forma pero sin reflejos? Al hacer eso, Dave descubrió que podía construir mosaicos progresivamente hacia afuera en un patrón que no se detenía y no se repetía.”

Pero entonces esta forma vino con una objeción diferente. Como explica Kaplan, si usas reflejos de Tile(1,1) el patrón sí se repite. En otras palabras, es periódico. Pero si Tile(1,1) se modifica reemplazando sus bordes rectos con curvas, se convierte en un einstein vampiro: una forma única que sin reflejo cubre el plano infinito en un patrón que nunca se puede hacer que se repita.

La pregunta obvia para los matemáticos y los entusiastas de los mosaicos es ¿qué sigue?

“Podemos plantear muchas variaciones del problema”, dice Kaplan. “Lo más interesante, al menos para mí, es si esto se puede hacer en 3D. Sería bueno tener una forma que se repita no periódicamente en tres dimensiones. Tales construcciones son mucho más difíciles de visualizar, pero computacionalmente no es mucho más difícil de probar si tuviéramos la suerte de encontrar una forma tridimensional, un poliforma, que al igual que el sombrero solo cubre aperiódicamente.”

“La teoría de los mosaicos como rama de las matemáticas es hermosa, tangible y tiene muchos problemas fascinantes por resolver. No hay escasez de trabajo de seguimiento por hacer.”

Hatfest, una celebración del descubrimiento de “el Sombrero”, tendrá lugar en el Instituto Matemático de la Universidad de Oxford del 20 al 21 de julio. El primer día del evento contará con charlas y talleres sobre mosaicos dirigidos a un público no especializado, mientras que el segundo contará con presentaciones dirigidas a un público amplio de físicos y matemáticos.

Para obtener más información, inicie sesión en nuestro sitio web https://international-maths-challenge.com

Crédito del artículo otorgado a Joe Petrik, Universidad de Waterloo

왼쪽에 있는 14면체 다각형 Tile(1,1)은 약한 카이랄 비주기적 모노타일로 알려져 있습니다. 즉, 반사되지 않은 타일과 반사된 타일이 혼합된 타일링이 금지된다면, 이 도형은 비주기적으로만 타일링됩니다. 하지만 중앙과 오른쪽에 보이는 것처럼 가장자리를 수정함으로써, 비주기적 타일링만 허용하는 “스펙터” 라고 불리는 엄격한 카이랄 비주기적 모노타일이 생성됩니다. 출처: 워털루 대학교

최근 체리턴 컴퓨터 과학 대학의 크레이그 카플란 교수도 포함된 4명으로 구성된 국제 연구팀은 무한한 2차원 표면인 평면을 결코 반복되지 않는 패턴으로 타일링하는 단 하나의 도형을 발견했습니다.

이 발견은 수학자, 타일링 애호가, 그리고 일반 대중 모두를 매료시켰습니다.

그들이 “모자” 라고 부르는 이 13면체 다각형은 수학자들에게 비주기적 모노타일 또는 “아인슈타인” 으로 알려져 있는데, 이는 “하나의 돌” 을 의미하는 독일어 단어입니다.

하지만 연구팀의 가장 최근 발견은 다시 한번 수준을 한 단계 더 끌어올렸습니다. 그들은 첫 번째 도형과 관련이 있으면서 훨씬 더 엄격한 정의를 충족하는 또 다른 도형을 발견했습니다. “스펙터” 라고 불리는 이 새로운 도형은 도형의 거울상을 사용하지 않고도 결코 반복되지 않는 패턴으로 평면을 타일링합니다. 이러한 이유로 이 도형은 “뱀파이어 아인슈타인”—즉, 반사를 요구하지 않고 비주기적으로 타일링하는 도형—이라고도 불립니다.

카플란 교수는 설명합니다. “저희의 첫 번째 논문은 아인슈타인 문제를 해결했지만, 그 도형이 비주기적으로 타일링하기 위해 반사를 필요로 했기 때문에 사람들은 정당한 질문을 제기했습니다. ‘모자가 하는 일을 반사 없이 할 수 있는 도형이 있을까?’” “저희는 이 하위 문제를 해결할 뿐만 아니라, 첫 번째 논문이 나온 지 얼마 되지 않아 이 문제를 해결하는 도형을 찾게 된 것이 큰 행운이었습니다.”

수학자들에게는 모자와 그 거울상은 하나의 도형이지만, 물리적인 세계에서는 왼손잡이 도형과 오른손잡이 도형은 다르게 행동할 수 있습니다. 예를 들어, 오른손 장갑을 왼손에 낄 수는 없습니다.

카플란 교수는 말합니다. “만약 한쪽 면이 유약 처리된 모자 모양의 타일로 넓은 욕실 바닥을 비주기적으로 타일링한다면, 모자와 모자의 거울상이 모두 필요할 것입니다.”

하지만 최근 발견을 촉발한 것은 이러한 사소한 논쟁이 아니었습니다.

뱀파이어 아인슈타인의 발견은 몇 달 전 그의 호기심이 원래의 아인슈타인 발견으로 이어졌던 영국 요크셔 출신의 은퇴한 인쇄 기술자이자 스스로를 도형 애호가라고 칭하는 데이비드 스미스의 생각에서 시작되었습니다.

카플란 교수는 말합니다. “저희의 모자 논문이 온라인에 공개된 지 며칠 후, 데이브는 관련 도형을 가지고 놀다가 이상하게 행동하는 것처럼 보였다고 이메일을 보냈습니다.” “MC 에셔의 정신을 이어받은 작품으로 유명한 일본 수학자이자 예술가인 아라키 요시아키가 Tile(1,1)의 사진을 올렸는데, 데이브가 그것을 더 자세히 살펴보는 데 관심을 갖게 되었습니다.”

요시아키는 트위터에 흥미로운 질문을 올렸습니다. “새로운 비주기적 모노타일 Tile(1, 1.1)을 기반으로 한 비주기적 거북이 테셀레이션. 이 타일링에서 약 12.7%의 타일이 반사된다고 합니다. 녹색 타일이 한 예시입니다. 타일링 안에 반사된 거북이가 하나 더 숨어 있습니다. 반사된 것은 누구일까요?”

“요시가 Tile(1,1)을 거북이로 만들었는데, 그 사진에서는 다른 반사된 거북이를 찾기가 좀 어렵습니다. 하지만 데이브는 호기심을 갖게 되었습니다. ‘이 도형으로 타일링하되 반사 없이 하면 어떨까?’ 그렇게 하면서 데이브는 멈추지 않고 반복되지 않는 패턴으로 타일링을 점진적으로 바깥쪽으로 확장해 나갈 수 있다는 것을 발견했습니다.”

하지만 그때 이 도형은 또 다른 문제점을 안고 있었습니다. 카플란 교수가 설명하듯이, Tile(1,1)의 반사된 형태를 사용하면 패턴은 반복됩니다. 다시 말해, 그것은 주기적입니다. 하지만 Tile(1,1)의 직선 가장자리를 곡선으로 대체하여 수정하면, 그것은 뱀파이어 아인슈타인—즉, 반사 없이 무한 평면을 결코 반복되지 않는 패턴으로 타일링하는 단 하나의 도형—이 됩니다.

수학자와 타일링 애호가들에게 명백한 질문은 ‘다음은 무엇인가?’입니다.

카플란 교수는 말합니다. “우리는 이 문제의 다양한 변형을 제시할 수 있습니다.” “적어도 저에게는 가장 흥미로운 점은 이것이 3D로도 가능한지 여부입니다. 3차원에서 비주기적으로 반복되는 도형이 있다면 좋을 것입니다. 그러한 구성은 시각화하기 훨씬 어렵지만, 만약 모자처럼 비주기적으로만 타일링되는 3차원 도형—폴리폼—을 찾을 수 있다면, 계산적으로 증명하는 것이 그렇게 훨씬 더 어렵지는 않을 것입니다.”

“수학의 한 분야로서 타일링 이론은 아름답고, 실질적이며, 해결해야 할 매혹적인 문제들이 많습니다. 앞으로 해야 할 후속 연구는 부족하지 않습니다.”

“모자” 의 발견을 기념하는 햇페스트(Hatfest)는 7월 20일부터 21일까지 옥스퍼드 대학교 수학 연구소에서 개최될 예정입니다. 행사 첫째 날에는 일반 대중을 대상으로 한 타일링 강연과 워크숍이 진행될 예정이며, 둘째 날에는 물리학자와 수학자 등 폭넓은 청중을 대상으로 한 발표가 있을 예정입니다.

더 많은 통찰력을 얻으려면 저희 웹사이트 https://international-maths-challenge.com에 접속하세요.

기사 제공: 워털루 대학교 조 페트릭

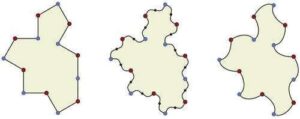
The 14-sided polygon Tile(1,1), on the left, is known as a weakly chiral aperiodic monotile — in other words, if tilings that mix unreflected and reflected tiles are forbidden, then it tiles only aperiodically. However, by modifying its edges, as shown in the centre and right, strictly chiral aperiodic monotiles called “spectres” are created that admit only non-periodic tilings. Credit: University of Waterloo

Recently, an international team of four, that includes Cheriton School of Computer Science professor Dr. Craig Kaplan, discovered a single shape that tiles the plane—an infinite, two-dimensional surface—in a pattern that can never be made to repeat.

The discovery mesmerized mathematicians, tiling enthusiasts and the public alike.

The shape, a 13-sided polygon they called “the hat,” is known to mathematicians as an aperiodic monotile or an “einstein,” the German words that mean “one stone.”

But the team’s most recent discovery has raised the bar once again. They found another shape, related to the first, that meets an even stricter definition. Dubbed the “specter,” the new shape tiles a plane in a pattern that never repeats without the use of mirror images of the shape. For this reason, it has also been called a “vampire einstein”—a shape that tiles aperiodically without requiring its reflection.

“Our first paper solved the einstein problem, but as the shape required reflection to tile aperiodically people raised a legitimate question: Is there a shape that can do what the hat does but without reflection,” Kaplan explains. “It was our good fortune that we found a shape that not only solves this subproblem, but also solved it so soon after the first paper.”

To mathematicians, the hat and its mirror image are a single shape, but in the physical world left-handed and right-handed shapes can behave differently. You can’t, for example, wear a right-handed glove on your left hand.

“If you tiled a large bathroom floor aperiodically with hat-shaped tiles that had been glazed on one side you would need hats and mirror images of hats,” Kaplan says.

But it was not this quibble that motivated the recent discovery.

The discovery of the vampire einstein began with the musings of David Smith, a retired print technician and self-described shape hobbyist from Yorkshire, England, whose curiosity months earlier led to the original einstein discovery.

“Dave emailed us a couple of days after our hat paper went online to say that he had been playing around with a related shape that seemed to be behaving strangely,” Kaplan says. “Yoshiaki Araki, a Japanese mathematician and well-known artist whose work is in the spirit of MC Escher, had posted pictures of Tile(1,1) that got Dave interested in looking at it further.”

Yoshiaki posted an intriguing question on Twitter: “An aperiodic turtle tessellation based on new aperiodic monotile Tile(1, 1.1). In the tiling, it is said that around 12.7% of tiles are reflected. The green one is an instance. One more reflected turtle is hidden in the tiling. Who is the reflected?'”

“Yoshi had turned Tile(1,1) into turtles and it’s a bit hard to see the other reflected turtle in that picture. But it got Dave curious. What if we tile with this shape but without reflections? As he did that, Dave found that he could build tilings progressively outward in a pattern that didn’t stop and didn’t repeat.”

But then this shape came with a different quibble. As Kaplan explains, if you use reflections of Tile(1,1) the pattern does repeat. In other words, it’s periodic. But if Tile(1,1) is modified by replacing its straight edges with curves, it becomes a vampire einstein—a single shape that without reflection tiles the infinite plane in a pattern that can never be made to repeat.

The obvious question for mathematicians and tiling enthusiasts is what’s next?

“We can pose many variations of the problem,” Kaplan says. “The most interesting, for me at least, is whether this can be done in 3D. It would be nice to have a shape that repeats non-periodically in three dimensions. Such constructions are much harder to visualize, but computationally it’s not that much more difficult to prove should we be so lucky as to find a three-dimensional shape—a polyform—that like the hat tiles only aperiodically.”

“Tiling theory as a branch of mathematics is beautiful, tangible, and has a lot of fascinating problems to be solved. There’s no shortage of follow-up work to be done.”

Hatfest, a celebration of the discovery of “the Hat,” will be taking place at the University of Oxford’s Mathematical Institute from July 20 to 21. The event’s first day will feature talks and workshops on tiling aimed at a lay audience, while the second will feature presentations aimed at a broad audience of physicists and mathematicians.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Joe Petrik, University of Waterloo

左侧的 14 边形 Tile(1,1) 被称为弱手性非周期性单瓦——换句话说，如果禁止混合未反射和反射瓦片的平铺，那么它只能非周期性地平铺。然而，通过修改其边缘，如中心和右侧所示，创建了称为 “spectres” 的严格手性非周期性单瓦，它们只允许非周期性平铺。图片来源：滑铁卢大学

最近，一个由四人组成的国际团队，其中包括切里顿计算机科学学院的 Craig Kaplan 博士，发现了一种可以平铺平面的单一形状——一个无限的二维表面——其图案永远无法重复。

这一发现让数学家、平铺爱好者和公众都为之着迷。

这种形状，一个 13 边形，他们称之为 “the hat”，在数学家眼中被称为非周期性单瓦或 “einstein”，这个德语单词的意思是 “one stone”。

但该团队最近的发现再次提高了标准。他们发现了另一种形状，与第一种形状相关，它符合更严格的定义。这种新形状被称为 “specter”，它以一种永不重复的模式平铺一个平面，而无需使用该形状的镜像。因此，它也被称为 “vampire einstein”——一种无需反射即可非周期性平铺的形状。

“我们的第一篇论文解决了 einstein 问题，但由于该形状需要反射才能非周期性地平铺，人们提出了一个合理的问题：是否存在一种形状可以像 hat 一样做到这一点，但无需反射，” Kaplan 解释说。“我们很幸运地找到了一个不仅解决了这个子问题，而且在第一篇论文之后不久就解决了它的形状。”

对于数学家来说，hat 及其镜像是一个单一的形状，但在物理世界中，左手和右手的形状表现可能不同。例如，你不能在左手上戴右手手套。

“如果你用一面上了釉的 hat 形瓷砖非周期性地铺设一个大型浴室地板，你需要 hat 和 hat 的镜像，” Kaplan 说。

但并非是这种吹毛求疵促成了最近的发现。

vampire einstein 的发现始于 David Smith 的沉思，他是一位退休的印刷技术员，也是一位来自英国约克郡的自称形状爱好者，几个月前他的好奇心促成了最初的 einstein 发现。

“在我们的 hat 论文上线几天后，Dave 给我们发了一封电子邮件，说他一直在摆弄一个相关的形状，这个形状的行为似乎很奇怪，” Kaplan 说。“日本数学家兼著名艺术家 Yoshiaki Araki 的作品具有 MC Escher 的精神，他发布了 Tile(1,1) 的图片，这引起了 Dave 对它的进一步关注。”

Yoshiaki 在 Twitter 上发布了一个有趣的问题：“基于新的非周期性单瓦 Tile(1, 1.1) 的非周期性海龟镶嵌。在镶嵌中，据说大约 12.7% 的瓷砖被反射。绿色的是一个例子。还有一个反射的海龟隐藏在镶嵌中。谁被反射了？”

“Yoshi 将 Tile(1,1) 变成了海龟，并且很难在该图片中看到另一个反射的海龟。但这引起了 Dave 的好奇。如果我们用这种形状平铺，但不进行反射呢？当他这样做时，Dave 发现他可以逐步向外构建平铺，其模式不会停止也不会重复。”

但随后这种形状出现了一个不同的问题。正如 Kaplan 解释的那样，如果你使用 Tile(1,1) 的反射，则该模式会重复。换句话说，它是周期性的。但是，如果通过用曲线替换其直线边缘来修改 Tile(1,1)，它就会变成 vampire einstein——一种无需反射即可在永不重复的模式中平铺无限平面的单一形状。

对于数学家和平铺爱好者来说，显而易见的问题是接下来会发生什么？

“我们可以提出许多问题的变体，” Kaplan 说。“至少对我来说，最有趣的是这是否可以在 3D 中完成。如果有一种形状可以在三个维度上非周期性地重复，那就太好了。这种结构更难可视化，但从计算上来说，证明我们是否足够幸运地找到一个三维形状（一种多形体）并不难，就像 hat 一样，它只能非周期性地平铺。”

“平铺理论作为数学的一个分支是美丽的、有形的，并且有很多有趣的问题需要解决。不乏后续工作要做。”

Hatfest 是对 “the Hat” 发现的庆祝活动，将于 7 月 20 日至 21 日在牛津大学数学研究所举行。该活动的第一天将以针对普通观众的关于平铺的讲座和研讨会为特色，而第二天将以针对广泛的物理学家和数学家观众的演讲为特色。

要了解更多此类见解，请登录我们的网站 https://international-maths-challenge.com

本文的作者是滑铁卢大学的 Joe Petrik

Investigadores del Centro de Investigación de Transformación Industrial ARC de la Universidad de Australia Occidental para la Transformación de la Infraestructura Energética a través de la Ingeniería Digital (TIDE) han logrado un importante avance matemático que podría ayudar a transformar la investigación y la tecnología oceánicas.

El investigador Dr. Lachlan Astfalck, de la Facultad de Física, Matemáticas e Informática de la UWA, y su equipo desarrollaron un nuevo método para la estimación de la densidad espectral, abordando sesgos de larga data y allanando el camino para estudios oceanográficos más precisos.

El estudio se publicó en la revista Biometrika, conocida por su énfasis en las contribuciones metodológicas y teóricas originales de valor directo o potencial en las aplicaciones.

“Comprender el océano es crucial para numerosos campos, incluida la ingeniería marina, la evaluación y modelado del clima, las tecnologías renovables, la defensa y el transporte”, dijo el Dr. Astfalck.

“Nuestro nuevo método permite a los investigadores y profesionales de la industria avanzar en las tecnologías oceánicas con mayor confianza y precisión.”

La estimación de la densidad espectral es una técnica matemática utilizada para medir la contribución energética de las señales oscilatorias, como las olas y las corrientes, mediante la identificación de las frecuencias que transportan la mayor cantidad de energía.

“Tradicionalmente, el estimador de Welch ha sido el método de referencia para este análisis debido a su facilidad de uso y amplia citación, sin embargo, este método tiene un riesgo inherente de sesgo, que puede distorsionar las estimaciones esperadas basadas en la suposición del modelo, un problema que a menudo se pasa por alto”, dijo el Dr. Astfalck.

El equipo de TIDE desarrolló el estimador de Welch no sesgado, que utiliza el aprendizaje estadístico no paramétrico para eliminar estos sesgos.

“Nuestro método mejora la precisión y la fiabilidad de los cálculos espectrales sin requerir suposiciones específicas sobre la forma o distribución de los datos, lo que es particularmente útil cuando se trata de datos complejos que no siguen patrones analíticos conocidos, como las mareas internas en las regiones de la plataforma oceánica”, dijo el Dr. Astfalck.

El nuevo método se aplicó recientemente en un proyecto de investigación de TIDE por el profesor titular de la Escuela de Posgrado de Océanos de la UWA y colaborador de TIDE, el Dr. Matt Rayson, para analizar procesos oceánicos no lineales complejos.

“El océano es difícil de medir y comprender, y el trabajo que estamos haciendo se centra en descubrir algunos de esos misterios”, dijo el Dr. Rayson.

El nuevo método significa que podemos comprender mejor los procesos oceánicos, los modelos climáticos, las corrientes oceánicas y el transporte de sedimentos, lo que nos acerca al desarrollo de la próxima generación de modelos oceánicos numéricos.

Para obtener más información como esta, visite nuestro sitio web en www.international-maths-challenge.com.

Crédito del artículo otorgado a la Universidad de Australia Occidental.

西澳大利亚大学 ARC 工业转型研究中心的研究人员通过数字工程改造能源基础设施 (TIDE)，取得了一项重大的数学突破，这可能有助于改变海洋研究和技术。

来自西澳大学物理、数学和计算学院的研究员 Lachlan Astfalck 博士及其团队开发了一种新的频谱密度估计方法，解决了长期存在的偏差问题，并为更准确的海洋学研究铺平了道路。

该研究发表在 Biometrika 杂志上，该杂志以强调在应用中具有直接或潜在价值的原创方法论和理论贡献而闻名。

Astfalck 博士说：“了解海洋对于包括海上工程、气候评估和建模、可再生技术、国防和运输在内的众多领域至关重要”。

“我们的新方法使研究人员和行业专业人士能够以更大的信心和准确性推进海洋技术。”

频谱密度估计是一种数学技术，用于通过识别哪些频率携带的能量最多来测量振荡信号（如波浪和海流）的能量贡献。

Astfalck 博士说：“传统上，Welch 估计器因其易用性和广泛引用而成为这种分析的首选方法，但是这种方法具有固有的偏差风险，这会根据模型的假设扭曲预期的估计值，这是一个经常被忽视的问题”。

TIDE 团队开发了去偏 Welch 估计器，该估计器使用非参数统计学习来消除这些偏差。

Astfalck 博士说：“我们的方法提高了频谱计算的准确性和可靠性，而无需对数据的形状或分布进行特定假设，这在处理不遵循已知分析模式的复杂数据时特别有用，例如海洋陆架区域的内潮”。

西澳大学海洋研究生院高级讲师兼 TIDE 合作者 Matt Rayson 博士最近在一个 TIDE 研究项目中应用了这种新方法，以研究复杂的非线性海洋过程。

Rayson 博士说：“海洋难以测量和理解，我们所做的工作都是为了揭开其中的一些谜团”。

“新方法意味着我们可以更好地了解海洋过程、气候模型、洋流和沉积物输送，从而使我们更接近于开发下一代数值海洋模型。

要了解更多此类见解，请访问我们的网站 www.international-maths-challenge.com。

本文的版权归西澳大利亚大学所有。