Month: February 2024

A new study into classroom practices, led by Dr. Steve Murphy, has found extensive research fails to uncover how teachers can remedy poor student engagement and perform well in math.

More than 3,000 research papers were reviewed over the course of the study, but only 26 contained detailed steps for teachers to improve both student engagement and results in math. The review is published in the journal Teaching and Teacher Education.

Dr. Murphy said the scarcity of research involving young childrenwas concerning.

“Children’s engagement in math begins to decline from the beginning of primary school while their mathematical identity begins to solidify,” Dr. Murphy said.

“We need more research that investigates achievement and engagement together to give teachers good advice on how to engage students in mathematics and perform well.

“La Trobe has developed a model for research that can achieve this.”

While teachers play an important role in making decisions that impact the learning environment, Dr. Murphy said parents are also highly influential in children’s math education journeys.

“We often hear parents say, ‘It’s OK, I was never good at math,’ but they’d never say that to their child about reading or writing,” Dr. Murphy said.

La Trobe’s School of Education is determined to improve mathematical outcomes for students, arguing it’s an important school subject that is highly applicable in today’s technologically rich society.

Previous research led by Dr. Murphy published in Educational Studies in Mathematics found many parents were unfamiliar with the modern ways of teaching math and lacked self-confidence to independently assist their children learning math during the COVID-19 pandemic.

“The implication for parents is that you don’t need to be a great mathematician to support your children in math, you just need to be willing to learn a little about how schools teach math today,” Dr. Murphy said.

“It’s not all bad news for educators and parents. Parents don’t need to teach math; they just need to support what their children’s teacher is doing.

“Keeping positive, being encouraging and interested in their children’s math learning goes a long way.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article to be given La Trobe Universit

Children’s interest in, and competence perceptions of, mathematics are generally quite positive as they begin school, but turn less positive during the first three years. Changes in interest and self-concept are also associated with each other. In other words, if a child’s interest fades, so does their competence perception, and vice versa.

This is shown by a recent study from Finland published in the British Journal of Educational Psychology that explores the development of children’s motivation for mathematics during the early school years and how that development is associated with their mathematics competence. The researchers followed nearly 300 children for three years.

“A significant observation was that both school beginners’ higher initial motivation, and less decline in motivation during the follow-up, predicted better competence in the third grade, after accounting for initial differences in competence,” says Professor Markku Niemivirta of the University of Eastern Finland.

There were no gender differences in school beginners’ motivation and competence, but at the end of the follow-up, girls’ motivation had, on average, declined more than that of boys.

Gendered development is starting to show

The study shows that children are able to assess their motivation for mathematics rather accurately already when beginning school. In addition, children’s assessments of their interest and competence are already differentiated, despite being closely related.

“It is only natural that children are more interested in things they feel good at. And vice versa, they may do better in something they’re interested in.”

On average however, school beginners’ positive motivation starts to decline during the early school years, and the scale of this decline is associated with later differences in competence. Although there are no gender differences in competence, girls’ more negative change in motivation on average reflects an unfortunate gendered development, the traces of which remain visible until much later.

Practices for maintaining interest and having experiences of success

Although the negative change observed in the study may partly reflect children’s more realistic self-assessment over time, the researchers suspect that a role is also played by mathematics gradually getting more difficult, and an emphasis being placed on performance.

“The observed association between a change in motivation and competence shows, however, the added value of positive interest and self-concept. It would be important to develop and apply teaching practices that support and maintain children’s interest in mathematics and strengthen their experiences of success,” Niemivirta says.

In the three-year study conducted by the Motivation, Learning and Well-being research collective, MoLeWe, children assessed their interest in, and competence perceptions of, mathematics annually. Mathematics competence was assessed by tests and teacher evaluations.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article to be given University of Eastern Finland

When the NBA celebrated the start of its 75th season in fall 2021, it was clear that the 3-point shot adopted by the league in 1979-80 had transformed the sport.

The number of attempts beyond the arc had increased in each of the previous 10 seasons, from 22.2% in 2010-11 to 39.2% in 2020-21, and it had been nearly five years since a team won a game without making at least one 3-pointer (that streak is now up to eight years). Led by 3-point specialists Steph Curry and Klay Thompson, the Golden State Warriors had won three of the previous seven NBA titles and were about to win a fourth in 2022.

It appeared that the 3-point revolution would never end. But a recent study by Falk College of Sport and Human Dynamics sport analytics professor Shane Sanders and associate professor Justin Ehrlich shows that while the number of 3-point shots continues to increase, the average expected value of 3-pointers has become less than 2-pointers since the 2017-18 season.

“When taking fouled shots and made free throws into consideration, we found that what had long been a premium for the 3-point shot started to become a dispremium in the 2017-18 season and that trend is continuing,” Ehrlich says. “The implication of these findings is enormous in terms of potential impact on roster construction and offensive philosophies.”

The research preprint from Sanders and Ehrlich, “Estimating NBA Team Shot Selection Efficiency from Aggregations of True, Continuous Shot Charts: A Generalized Additive Model Approach,” is available through the Social Science Research Network website. Sanders and Ehrlich will present their paper as one of seven finalists in the research competition at the NBA-centric MIT Sloan Sports Analytics Conference March 1-2 in Boston, Massachusetts.

“In past conferences, there has been a lot of discussion among NBA executives about how basketball analytics created the 3-point ‘moneyball’ era of basketball and how this has impacted the popularity of the game,” Sanders says. “Perhaps ironically, our research uses basketball analytics, along with a fully specified team offensive objective function, to say there is now too much 3-point shooting for a point-maximizing offense.”

To conduct their research, Sanders and Ehrlich developed a new shot chart that uses a generalized additive model to estimate total shot proficiency continuously in the half-court. Their shot chart incorporates missed shots that draw a shooting foul—and shot-pursuant free throw scoring—to determine total scoring yield following a shot decision.

Current expected value formulas fall short by not including this additional information, which, when combined with the outcome of the initial shot attempt, results in what Sanders and Ehrlich call the “true point value” of a shot. For the 2022-23 NBA season:

• True Value from 2-point shot attempts=1.181
• True Value from 3-point shot attempts=1.094

And even when not factoring in free throws, the researchers found that the expected value from 3-point shots are now worth less than 2-point shots. For the 2022-23 NBA season:

• Expected value from 2P field goal attempt=2P% * 2 = .548 * 2= 1.096
• Expected value from 3P field goal attempt=3P% * 3 = .361 * 3= 1.083

The true value data can be found in this dashboard, and the graph above shows the expected and true values of 2- and 3-point shots from 2016-22.

According to this research, the expected value from average 2-point field goal attempts (FGA) is now worth 0.013 points more than average 3-point FGA, even before factoring in shot-pursuant free throw scoring. In other words, if you multiply the probability of making a 3-point FGA times the value of a 3-point FGA, it’s worth less than if you multiple a 2-point FGA times the value of a 2-point FGA.

When discussing true point value, the researchers use the term “shot attempts” instead of “field goal attempts” because their formula includes missed shots when a player is fouled, which is not included in standard field-goal attempt statistics. So, when including made and missed free throws, the disparity based on this new true value metric is even greater as average 2-point shot attempts are now worth 0.087 more points than 3-point shot attempts.

Officials from NBA teams and the league have discussed moving the 3-point line back from its current distance of 23 feet, 9 inches (22 feet in the corners). But as this study shows, the value of a 3-pointer is decreasing at the current distance, and teams are already starting to alter their shot selection to emphasize more high-percentage 2-point shots.

“These research findings do not coincide completely with the unresearched musings of NBA analysts Charles Barkley and Shaquille O’Neal,” Sanders says.

“For example, our findings do not suggest that such perimeter stars as Stephen Curry or Damian Lillard should not shoot a lot of threes. It means marginal stretch fours and other marginal outside shooters should not pull up for a 3 as often and that some marginal outside shooters should not extend their range to 25-26 feet or more. Players can still achieve the offensive spacing benefits of positioning on the perimeter without some players shooting from there quite as often.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Matt Michael, Syracuse University

Researchers from the University of Oulu, Finland, investigated how air pollution affects students’ performance in matriculation exams, particularly in mathematical subjects. The study revealed that performance declines in exams involving thinking and memorization when fine particulate matter (PM2.5) levels in the school’s vicinity increase even slightly.

The research is the first to examine the same student’s performance in a test measuring the same skill in a short time frame. Skills refer to linguistic and mathematical abilities, measured by exams in the Finnish language, writing, reading, mathematics, and physics.

Researchers from the University of Oulu Business School examined the effects of very short-term exposure to air pollution on students’ performance in matriculation exams in Finland from 2006 to 2016.

According to the study, a one-unit increase in PM2.5 particle concentration (particles smaller than 2.5 micrometers) reduced the average student’s performance in a mathematical exam by approximately 0.13 percentage points compared to performance in a similar exam with lower fine particulate concentrations.

The study found no impact on linguistic skills due to an increase in fine particulate matter, and there were no gender differences observed.

Researchers were surprised to find significant effects on matriculation exam performance in Finland, a country with relatively low air pollution levels. This is the first time such effects have been demonstrated in Finland. The researchers emphasize that even in countries like Finland, where air pollution levels generally comply with the World Health Organization’s recommendations, reducing air pollution remains crucial.

“Increasing evidence suggests that exposure to air pollution during exams may have a decisive impact on the progression of students into further studies, especially if matriculation exam results are used as a significant selection criterion,” says University Researcher Marko Korhonen.

The primary data for the study came from Statistics Finland, covering all matriculation exams in Finland from spring 2006 to autumn 2016, including 22 academic terms. The study included over 370,000 final exams from Finnish high schools, involving 172,414 students from 253 schools in 54 municipalities.

Student performance was assessed using hourly air quality measurements from monitoring points located near the exam venues. The structure of Finnish high school final exams, where students take multiple exams in different courses, allowed the examination of each student’s test results in various final exams. Exams were conducted on different days in the same schools, and air quality was measured during the exams near each school.

The study, titled “The impact of ambient PM2.5 air pollution on student performance: Evidence from Finnish matriculation examinations,” has been published in Economics Letters.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to University of Oulu

Conventional wisdom says that you should never leave money on the table when negotiating. But research in my field suggests this could be exactly the wrong approach.

There’s mounting evidence that a short-term win at the bargaining table can mean a loss in terms of overall trust and cooperation. That can leave everyone—including the “winner”—worse off.

As a former executive, I’ve managed large contracts as both a buyer and a seller. Now, as a business professor, I study these trading partner relationships, exploring what works in practice. My work supports what economic theorists and social scientists have been arguing for years: The best results come when people collaborate to create long-term value instead of fighting for short-term wins.

What game are you playing?

Research into art, science and practice of collaborative approaches dates back to the 1940s when the mathematician John von Neumann and economist Oskar Morgenstern used mathematical analysis to model competition and cooperation in living things.

Interest in collaborative approaches grew when researchers John Nash, John C. Harsanyi and Reinhard Selten won a Nobel Memorial Prize in Economic Sciences in 1994. Their work inspired academics around the world to delve deeper into what’s known as game theory.

Game theory is the study of the outcome of strategic interactions among decision makers. By using rigorous statistical methods, researchers can model what happens when people choose to cooperate or choose to take an aggressive, power-based approach to negotiation.

Many business leaders are taught strategies focusing on using their power and playing to win—often at the other party’s expense. In game theory, this is known as a zero-sum game, and it’s an easy trap to fall into.

But not every game has a clear winner or loser. In economics, a win-win game is called a nonzero-sum game. In this sort of situation, people aren’t fighting over whose slice of a pie will be larger. They’re working to grow the pie for everyone.

Kate Vitasek lays out five rules for developing a value creation strategy.

A second dimension of game theory is whether people are playing a one-shot or a repeated game. Think of a one-shot game as like going to the flea market: You probably won’t see your trading partner again, so if you’re a jerk to them, the risk of facing the consequences is low.

An interesting twist uncovered by studying repeated games is that when one party uses their power in a negotiation, it creates the urge for the other party to retaliate.

The University of Michigan’s Robert Axelrod, a mathematician turned game theorist, coined this a “tit-for-tat” strategy. His research, perhaps best known in the book “The Evolution of Cooperation,” uses statistics to show that when individuals cooperate, they come out better than when they don’t.

The case for leaving money on the table

Another Nobel laureate, American economist Oliver Williamson, has offered negotiating advice that most would call a paradigm shift—and some, a heresy.

That advice? Always leave money on the table—especially when you’ll be returning to the same “game” again. Why? According to Williamson, it sends a powerful signal of trustworthiness and credibility to one’s negotiating partner when someone consciously chooses to cooperate and build trust.

The opposite approach leads to lost trust and what the Nobel laureate economist Oliver Hart calls “shading.” This is a retaliatory behaviour that happens when a party isn’t getting the outcome it expected from a deal and feels the other party is to blame.

Simply put, noncollaborative approaches causes distrust and create friction, which adds transaction costs and inefficiencies.

The million-dollar question is whether collaborative approaches work in practice. And from my vantage point as a scholar, the answer is yes. In fields as diverse as health care to high-tech, I see growing real-world evidence backing up the insights of game theory.

The lessons are simple yet profound: Playing a game together to achieve mutual interests is better than playing exclusively with self-interest in mind.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Kate Vitasek, The Conversation

Are cultural evolution rates similar across human societies? The emerging field of Cliodynamics uses mathematical models to study history.

Tobias Wand and colleagues used a data-driven approach to estimate the rates of cultural evolution in 23 geographic areas, using data from Seshat: Global History Databank, which records nine “complexity characteristics” for 370 polities over 10,000 years, ending in the nineteenth century. The work is published in the journal PNAS Nexus.

The complexity characteristics are polity population; extent of polity territory; the size of the largest urban center; hierarchical complexity; the presence of professional soldiers, officers, priests, bureaucrats, and judges; the variety of observable structures; characteristics of writing and recordkeeping; variety of types of texts; and monetary system.

The authors focused on 23 Natural Geographic Areas (NGAs) and restricted their analysis to the central part of each NGA’s timeline so that they could focus on periods of steady, uninterrupted growth rather than moments of invasion or civilization-ending crisis. A universal logistic growth model was fitted to a variable combining all nine complexity characteristics.

On average, it takes societies that develop in isolation about 2,500 years to reach high levels of social complexity, according to the authors. Full development of complexity was spread out over multiple cultural or institutional phases in every NGA.

According to the authors, the data suggest that there are common pathways in human social evolution across cultures.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to PNAS Nexus

In Lewis Carroll’s Through the Looking-Glass, the Red Queen tells Alice, “It takes all the running you can do, to keep in the same place.” The race between innovation and obsolescence is like this.

Recent evidence about the slowing of technological and scientific progress in contrast to the accelerating epidemiological risks in a globalized world—in the opposite direction—indicates the importance of the relative rates of innovation and obsolescence.

When does innovation outpace, or fail to outpace, obsolescence? Understanding this dynamic is nascent, and the way that innovation is discussed is largely fragmented across fields. Despite some qualitative efforts to bridge this gap, insights are rarely transferred.

In research led by Complexity Science Hub (CSH), Eddie Lee and colleagues have taken an important step towards building those bridges with a quantitative mathematical theory that models this dynamic.

The paper, “Idea engines: Unifying innovation & obsolescence from markets & genetic evolution to science,” is published in Proceedings of the National Academy of Sciences.

“You could say this is an exercise in translation,” says Lee, the first author of the paper. “There’s a plethora of theories on innovation and obsolescence in different fields: from economist Joseph Schumpeter’s theory of innovation, to other ideas proposed by theoretical biologist Stuart Kauffman, or philosopher of science Thomas Kuhn. Through our work, we try to open the doors to the scientific process and connect aspects of the different theories into one mathematical model,” explains Lee, a postdoc researcher at CSH.

Space of the possible, and its boundaries

Lee, together with Geoffrey West and Christopher Kempes at the Santa Fe Institute, conceives of innovation as expanding the space of the possible while obsolescence shrinks it. The “space of the possible” encompasses the set of all realized potentialities within a system.

“Within the space of the possible, you might think of different manufacturing technologies available in firms. All the living mutation species would be a good example in biology. In science, you might think of scientific theories that are feasible and empirically supported,” says Lee.

The space of the possible grows as innovations are pulled in from the “adjacent possible,” Stuart Kauffman’s term for the set of all things that lie one step away from what is possible. Lee and his co-authors compare this with an obsolescent front, which is the set of all things that are on the verge of being discarded.

Three possible scenarios

Based on this picture of the space of the possible, the team modeled a general dynamics of innovation and obsolescence to identify three possible scenarios. There is an ever-expanding scenario, where the possibilities agents are capable of growth without end. Schumpeterian dystopia is the opposite of this world, where innovation fails to outpace obsolescence. A third scenario follows the original Schumpeterian concept of creation and destruction, in which new ways of production survive by eliminating old ones.

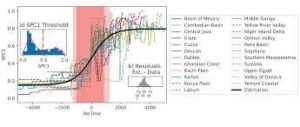
The model was tested with real-world data from a variety of fields, from measures of firm productivity to COVID-19 mutations and scientific citations. Thus, the researchers were able to bring together examples that have heretofore been considered in isolation from one another. Both the model and the data are for the average set of dynamics rather than focusing on specific innovations, which allows for the generalization emphasized in the paper.

“We saw a remarkable similarity between all the data, from economics, biology, and science of science,” states the CSH researcher. One key discovery is that all the systems seem to live around the innovative frontier. “Moreover, agents at the boundary of innovative explosion, whether close to it or far away, share the same characteristic profile,” adds Lee, where few agents are innovative and many are near obsolescence. West likens this to systems living on the “edge of chaos,” where a small change in the dynamics can lead to a large change in the state of the system.

Universal phenomenon

The novel approach could transform our understanding of the dynamics of innovation in complex systems. By trying to capture the essence of innovation and obsolescence as a universal phenomenon, the work brings divergent viewpoints together into a unified mathematical theory. “Our framework provides a way of unifying a phenomenon that has so far been studied separately with a quantitative theory,” say the authors.

“Given the critical role that innovation in all its multiple manifestations plays in society, it’s quite surprising that our work appears to be the first attempt to develop a sort of grand unified mathematical theory which is testable to understand its dynamics,” says West. “It’s still very crude but hopefully can provide a point of departure for developing a more detailed realistic theory that can help inform policy and practitioners.”

“We provide an average model of the combined dynamics of innovation and obsolescence,” says Kempes. “In the future it is exciting and important to think about how this average model meets up with detailed theories of how innovations actually occur. For example, how do current objects or technologies get combined to form new things in something like the recently proposed Assembly Theory?”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Complexity Science Hub

Converting hundreds of compositions by Johann Sebastian Bach into mathematical networks reveals that they store lots of information and convey it very effectively.

Johann Sebastian Bach is considered one of the great composers of Western classical music. Now, researchers are trying to figure out why – by analysing his music with information theory.

Suman Kulkarni at the University of Pennsylvania and her colleagues wanted to understand how the ability to recall or anticipate a piece of music relates to its structure. They chose to analyse Bach’s opus because he produced an enormous number of pieces with many different structures, including religious hymns called chorales and fast-paced, virtuosic toccatas.

First, the researchers translated each composition into an information network by representing each note as a node and each transition between notes as an edge, connecting them. Using this network, they compared the quantity of information in each composition. Toccatas, which were meant to entertain and surprise, contained more information than chorales, which were composed for more meditative settings like churches.

Kulkarni and her colleagues also used information networks to compare Bach’s music with listeners’ perception of it. They started with an existing computer model based on experiments in which participants reacted to a sequence of images on a screen. The researchers then measured how surprising an element of the sequence was. They adapted information networks based on this model to the music, with the links between each node representing how probable a listener thought it would be for two connected notes to play successively – or how surprised they would be if that happened. Because humans do not learn information perfectly, networks showing people’s presumed note changes for a composition rarely line up exactly with the network based directly on that composition. Researchers can then quantify that mismatch.

In this case, the mismatch was low, suggesting Bach’s pieces convey information rather effectively. However, Kulkarni hopes to fine-tune the computer model of human perception to better match real brain scans of people listening to the music.

“There is a missing link in neuroscience between complicated structures like music and how our brains respond to it, beyond just knowing the frequencies [of sounds]. This work could provide some nice inroads into that,” says Randy McIntosh at Simon Fraser University in Canada. However, there are many more factors that affect how someone perceives music – for example, how long a person listens to a piece and whether or not they have musical training. These still need to be accounted for, he says.

Information theory also has yet to reveal whether Bach’s composition style was exceptional compared with other types of music. McIntosh says his past work found some general similarities between musicians as different from Bach as the rock guitarist Eddie Van Halen, but more detailed analyses are needed.

“I would love to perform the same analysis for different composers and non-Western music,” says Kulkarni.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Karmela Padavic-Callaghan*

The springtime emergence of vast swarms of cicadas can be explained by a mathematical model of collective decision-making that has similarities to models describing stock market crashes.

Pick almost any location in the eastern United States—say, Columbus Ohio. Every 13 or 17 years, as the soil warms in springtime, vast swarms of cicadas emerge from their underground burrows singing their deafening song, take flight and mate, producing offspring for the next cycle.

This noisy phenomenon repeats all over the eastern and southeastern U.S. as 17 distinct broods emerge in staggered years. In spring 2024, billions of cicadas are expected as two different broods—one that appears every 13 years and another that appears every 17 years—emerge simultaneously.

Previous research has suggested that cicadas emerge once the soil temperature reaches 18°C, but even within a small geographical area, differences in sun exposure, foliage cover or humidity can lead to variations in temperature.

Now, in a paper published in the journal Physical Review E, researchers from the University of Cambridge have discovered how such synchronous cicada swarms can emerge despite these temperature differences.

The researchers developed a mathematical model for decision-making in an environment with variations in temperature and found that communication between cicada nymphs allows the group to come to a consensus about the local average temperature that then leads to large-scale swarms. The model is closely related to one that has been used to describe “avalanches” in decision-making like those among stock market traders, leading to crashes.

Mathematicians have been captivated by the appearance of 17- and 13-year cycles in various species of cicadas, and have previously developed mathematical models that showed how the appearance of such large prime numbers is a consequence of evolutionary pressures to avoid predation. However, the mechanism by which swarms emerge coherently in a given year has not been understood.

In developing their model, the Cambridge team was inspired by previous research on decision-making that represents each member of a group by a “spin” like that in a magnet, but instead of pointing up or down, the two states represent the decision to “remain” or “emerge.”

The local temperature experienced by the cicadas is then like a magnetic field that tends to align the spins and varies slowly from place to place on the scale of hundreds of meters, from sunny hilltops to shaded valleys in a forest. Communication between nearby nymphs is represented by an interaction between the spins that leads to local agreement of neighbours.

The researchers showed that in the presence of such interactions the swarms are large and space-filling, involving every member of the population in a range of local temperature environments, unlike the case without communication in which every nymph is on its own, responding to every subtle variation in microclimate.

The research was carried out Professor Raymond E Goldstein, the Alan Turing Professor of Complex Physical Systems in the Department of Applied Mathematics and Theoretical Physics (DAMTP), Professor Robert L Jack of DAMTP and the Yusuf Hamied Department of Chemistry, and Dr. Adriana I Pesci, a Senior Research Associate in DAMTP.

“As an applied mathematician, there is nothing more interesting than finding a model capable of explaining the behaviour of living beings, even in the simplest of cases,” said Pesci.

The researchers say that while their model does not require any particular means of communication between underground nymphs, acoustical signaling is a likely candidate, given the ear-splitting sounds that the swarms make once they emerge from underground.

The researchers hope that their conjecture regarding the role of communication will stimulate field research to test the hypothesis.

“If our conjecture that communication between nymphs plays a role in swarm emergence is confirmed, it would provide a striking example of how Darwinian evolution can act for the benefit of the group, not just the individual,” said Goldstein.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Sarah Collins, University of Cambridge

Have you ever wondered about the best way to pack a finite number of identical spheres into a shape-shifting flexible container, like a convex hull?

Researchers from the University of Twente, Active Soft Matter Lab led by Dr. Hanumantha Rao Vutukuri in the TNW Faculty, along with Utrecht University, have investigated this fascinating mathematical sphere-packing problem by combining experiments and computer simulations. Their research has been published in Nature Communications.

An intuitively simple problem concerning the best way to pack a set of spheres has a long history of studies dating back to the 17th century. The British sailor Raleigh, for instance, contemplated this issue while trying to find an efficient method for stacking cannonballs on his ship.

Later, Kepler conjectured that the densest packing for an infinite number of spheres would be the face-centered cubic (FCC) crystal structure, akin to the hexagonal arrangement of oranges and apples seen in supermarkets. Remarkably, this hypothesis was only proven in the 21st century.

The ‘sausage catastrophe’

When you have a finite number of spheres, everything gets more complicated; surprisingly, packing the “finite” spheres in a compact cluster does not always yield the densest packing. Mathematicians already conjectured decades ago that a linear, sausage-like arrangement provides the best packing, however, not for all numbers of spheres.

There’s a peculiar phenomenon at play: The sausage-shaped arrangement is the most efficient packing, but only with up to 55 spheres. Beyond that number, a clustered arrangement becomes the best packing. This abrupt transition is known as the “sausage catastrophe.”

In three-dimensional space, packing up to 55 spheres linearly forms a “sausage” that is denser than any cluster arrangement. However, in four dimensions, this scenario changes dramatically. About 300,000 spheres are needed for the “sausage” to transform into a spherelike cluster.

Rao was curious about whether this fundamentally intriguing problem could be observed and resolved in the lab using a model system. This system includes micron-sized spherical particles (colloids) and giant unilamellar vesicles (GUVs), which serve as flexible containers that are the main ingredients in Vutukuri’s lab.

“This curiosity led us to explore the finite sphere packing problem through experiments in 3D real space, specifically using colloids in GUVs. By varying the number of particles and the volume of the vesicles, we were able to examine the different particle arrangements inside these vesicles using a confocal microscope.

“We identified stable arrangements for specific combinations of vesicle volume and particle number: 1D (sausage), 2D (plate, with particles in one plane), and 3D (cluster). Notably, we also observed bistability; the configurations alternated between 1D and 2D arrangements or between 2D and 3D structures. However, our experiments were limited to observing a maximum of nine particles, as packing a larger number of particles resulted in the rupture of the vesicles.”

Vutukuri says that they then contacted Dijkstra’s lab at Utrecht University to delve deeper into this problem using simulations. Strikingly, the simulations predicted that packing spheres in a sausage configuration is most efficient for up to 55 spheres. However, when they attempted to pack 56 spheres into a vesicle, they discovered that a compact three-dimensional cluster was the more efficient arrangement.

Remarkably, for 57 spheres, the packing reverted back to a sausage configuration. While mathematicians have previously determined that a sausage configuration is the most efficient for 58 and 64 spheres, their study contradicts this, demonstrating that compact clusters are more effective.

The findings show that the “sausage catastrophe,” a phenomenon previously described by mathematicians, is not just a theoretical scenario but can also be observed experimentally.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to University of Twente