Month: October 2023

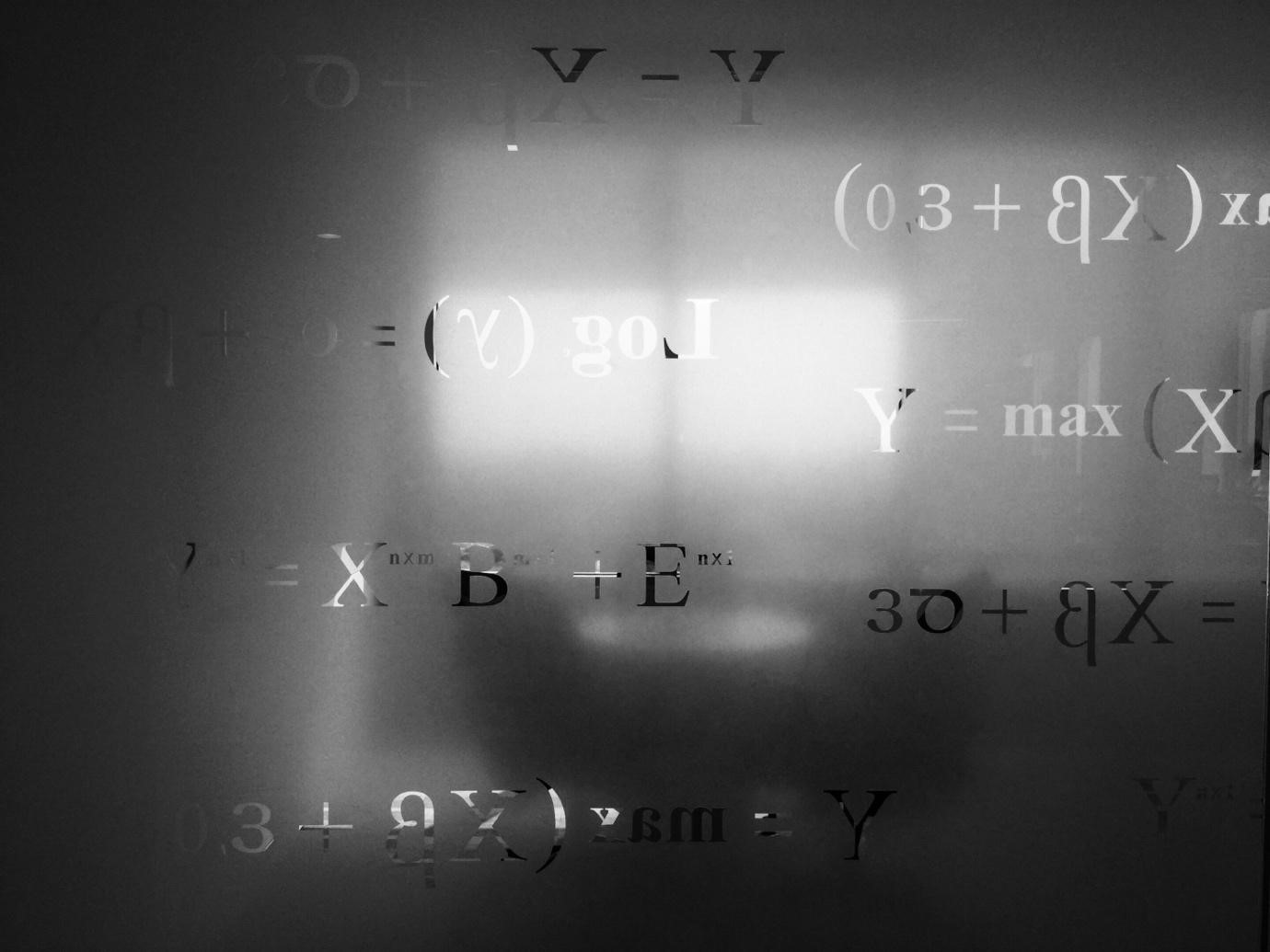
Economists from RUDN University have created a methodology based on mathematical modeling to manage production effectively with rapidly emerging innovations. The resultswere published in Sustainability.

Innovative products emerge so rapidly that enterprises have to change and adjust their management policies. Moreover, new management methods must ensure sustainable development. RUDN economists used mathematical modeling methods to develop a management methodology for enterprises that produce innovative products.

“An effective methodological tool for managing economic processes that ensure sustainable economic development of enterprises has not yet been developed. We set a goal to create such a tool based on mathematical modeling. Based on this tool, decision-makers could regulate processes, allocating additional resources and reducing risks,” said Zhanna Chupina, Ph.D., Associate Professor of the Department of Customs Affairs at RUDN University.

Economists have developed a tool that will allow, in modern conditions, to manage economic processes in such a way as to ensure sustainable development. To do this, the authors used mathematical modeling—they identified the main characteristics of the creation of innovative products and the activities of companies and described the dependence of profit on them. Economists included, for example, technical superiority over competitors, scientific and technological achievements based on the product, and price compliance with the capabilities of the buyer as the main values.

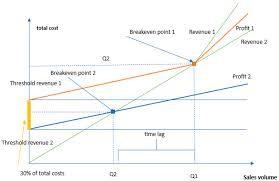
RUDN economists concluded that any innovation in a product is associated with the use or modernization of means of production. The authors determined the values of the technological level and the moments at which modernization should be carried out. It turned out that this needs to be done before the break-even point occurs, that is, the sales volume at which the proceeds from the sale of goods are equal to the costs of their production.

The general algorithm that economists have proposed is based on the fact that the properties of innovative products are involved in management. After management actions, it is necessary to evaluate the characteristics of the product and answer whether it is innovative. If so, then such an enterprise is considered capable of achieving global competitive superiority in the market. If not, then the characteristics need to be changed and return to the previous step.

“We have shown that for an organization to be in constant sustainable economic development, it is necessary to carry out updates to already produced innovative products even before the break-even point. We proposed a methodological toolkit to effectively manage the creation and production of innovative products and their renewal,” said Zhanna Chupina, Ph.D., associate professor of the Department of Customs Affairs at RUDN University.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Russian Foundation for Basic Research

Politicians in the UK have maths on the mind. The Conservatives intend to extend compulsory maths education for young people until 18.

And at the Labour party conference, shadow education secretary Bridget Phillipson announced the opposition’s plans to improve maths skills across the country: a focus on primary school and pre-school education rather than post-16, with an emphasis on children learning the maths they will need for everyday life.

Paying attention to young children’s maths is a good idea. Evidence from the UK and beyond shows that children start primary school with varying levels of mathematical skills – and disadvantage gaps are already evident at this point, meaning that children from poorer backgrounds may not have skills at the same level as their more well-off peers.

The differences between children’s maths skills then remain remarkably stable over time. Children who start primary school with mathematical abilities behind the level of their peers will typically remain behind their peers throughout school.

To reduce these gaps, we need to act early. But positive change won’t be achieved simply by adding more content to the primary or early years mathematics curriculums. Neither is it helpful to push children to learn more complex mathematics earlier. These approaches might lead to children learning maths in a superficial and rote manner, rather than understanding the underlying ideas.

Primary focus

Labour has raised the prospect of creating a “phonics for maths”. Phonics is a method of learning to read that teaches children the sounds that letters and combinations of letters make. It is required in primary schools, and pupils take a phonics screening check in year one to assess their progress.

Although not universally supported, phonics has been linked to improvements in reading levels among children in England.

However, phonics is a specific technique for teaching word reading, while mathematics is incredibly broad. It involves multiple skills as well as different types of knowledge and understanding.

Even in early primary school, mathematics is complex. Children need to understand quantities and their relationships, to recognise digits and understand place value, to carry out arithmetic procedures, to identify patterns in numbers and shapes, and much more. It is unlikely that a single technique, as phonics is, can underpin this breadth of knowledge and understanding.

But in another sense, the parallel with phonics is encouraging. The phonics revolution was informed by research and developed from a better understanding of how children learn to read. This can and should be emulated for mathematics. Research evidence on the early stages of learning maths can help build a solid approach to teaching mathematical skills to young children.

Another feature of Labour’s plans is their aim to “bring maths to life” by using real-world examples: budgeting, exchange rates, sports league tables.

A desire to give meaning to numbers and mathematics by building on children’s experiences is a good ambition. This can be achieved through play-based and hands-on activities, which involve children manipulating objects such as counters and cards to better understand mathematical ideas and relationships. It is also important to help children see numbers and mathematical patterns in the world around them: the number of red cars on the street or the shapes of windows and doors, for instance.

These approaches may provide a stronger foundation for future learning than focusing on using written digits or learning mathematical facts (such as 2 + 3 = 5) too early.

Taking care

But care is needed to ensure that bringing maths to life truly reflects children’s experiences and doesn’t become a gimmick. It could even increase disadvantage gaps due to differences in children’s experiences, for example, for children from families who lack access to bank accounts or have never had the experience of travelling abroad and using different currency.

There are already good examples out there of how to teach in this way – such as the Mastering Number programme. Any curriculum changes need to be properly funded and developed in collaboration with experts in the field.

Giving children better mathematical foundations through engaging and meaningful activities can set them up for success throughout school and beyond. This would not only positively affect children’s achievement but could also change attitudes to mathematics for the better.

Changing attitudes to mathematics from the foundations upwards can help children and young people feel confident and engaged with the subject and see its value in their life, leading to more wanting to study the subject.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to NadyaEugene/Shutterstock

Atomic shapes are so simple that they can’t be broken down any further. Mathematicians are trying to build a “periodic table” of these shapes, and they hope artificial intelligence can help.

Mathematicians attempting to build a “periodic table” of shapes have turned to artificial intelligence for help – but say they don’t understand how it works or whether it can be 100 per cent reliable.

Tom Coates at Imperial College London and his colleagues are working to classify shapes known as Fano varieties, which are so simple that they can’t be broken down into smaller components. Just as chemists arranged elements in the periodic table by their atomic weight and group to reveal new insights, the researchers hope that organising these “atomic” shapes by their various properties will help in understanding them.

The team has assigned each atomic shape a sequence of numbers derived from features such as the number of holes it has or the extent to which it twists around itself. This acts as a bar code to identify it.

Coates and his colleagues have now created an AI that can predict certain properties of these shapes from their bar code numbers alone, with an accuracy of 98 per cent – suggesting a relationship that some mathematicians intuitively thought might be real, but have found impossible to prove.

Unfortunately, there is a vast gulf between demonstrating that something is very often true and mathematically proving that it is always so. While the team suspects a one-to-one connection between each shape and its bar code, the mathematics community is “nowhere close” to proving this, says Coates.

“In pure mathematics, we don’t regard anything as true unless we have an actual proof written down on a piece of paper, and no advances in our understanding of machine learning will get around this problem,” says team member Alexander Kasprzyk at the University of Nottingham, UK.

Even without a proven link between the Fano varieties and bar codes, Kasprzyk says that the AI has let the team organise atomic shapes in a way that begins to mimic the periodic table, so that when you read from left to right, or up and down, there seem to be generalisable patterns in the geometry of the shapes.

“We had no idea that would be true, we had no idea how to begin doing it,” says Kasprzyk. “We probably would still not have had any idea about this in 50 years’ time. Frankly, people have been trying to study these things for 40 years and failing to get to a picture like this.”

The team hopes to refine the model to the point where missing spaces in its periodic table could point to the existence of unknown shapes, or where clustering of shapes could lead to logical categorisation, resulting in a better understanding and new ideas that could create a method of proof. “It clearly knows more things than we know, but it’s so mysterious right now,” says team member Sara Veneziale at Imperial College London.

Graham Niblo at the University of Southampton, UK, who wasn’t involved in the research, says that the work is akin to forming an accurate picture of a cello or a French horn just from the sound of a G note being played – but he stresses that humans will still need to tease understanding from the results provided by AI and create robust and conclusive proofs of these ideas.

“AI has definitely got uncanny abilities. But in the same way that telescopes didn’t put astronomers out of work, AI doesn’t put mathematicians out of work,” he says. “It just gives us a new tool that allows us to explore parts of the mathematical landscape that were out of reach, or, like a microscope, that were too obscure for us to notice with our current understanding.”

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Matthew Sparkes *

Five secret phrases used to create the encryption algorithms that secure everything from online banking to email have been lost to history – but now cryptographers are offering a bounty to rediscover them.

Could you solve a cryptography mystery?

Secret phrases that lie at the heart of modern data encryption standards were accidentally forgotten decades ago – but now cryptographers are offering a cash bounty for anyone who can figure them out. While this won’t allow anyone to break these encryption methods, it could solve a long-standing puzzle in the history of cryptography.

“This thing is used everywhere, and it’s an interesting question; what’s the full story? Where did they come from?” says cryptographer Filippo Valsorda. “Let’s help the trust in this important tool of cryptography, and let’s fill out this page of history that got torn off.”

The tool in question is a set of widely-used encryption algorithms that rely on mathematical objects called elliptic curves. In theory, any of an infinite number of curves can be used in the algorithms, but in the late 1990s the US National Security Agency (NSA), which is devoted to protecting domestic communications and cracking foreign transmissions, chose five specific curves it recommended for use. These were then included in official US encryption standards laid down in 2000, which are still used worldwide today.

Exactly why the NSA chose these particular curves is unclear, with the agency saying only that they were chosen at random. This led some people to believe that the NSA had secretly selected curves that were weak in some way, allowing the agency to crack them. Although there is no evidence that the elliptic curves in use today have been cracked, the story persists.

In the intervening years, it has been confirmed that the curves were chosen by an NSA cryptographer named Jerry Solinas, who died earlier this year. Anonymous sources have suggested that Solinas chose the curves by transforming English phrases into a string of numbers, or hashes, that served as a parameter in the curves.

It is thought the phrases were along the lines of “Jerry deserves a raise”. But rumours suggest Solinas’s computer was replaced shortly after making the choice, and keeping no record of them, he couldn’t figure out the specific phrases that produced the hashes used in the curves. Turning a phrase into a hash is a one-way process, meaning that recovering them was impossible with the computing power available at the time.

Dustin Moody at the US National Institute of Standards and Technology, which sets US encryption standards, confirmed the stories to New Scientist: “I asked Jerry Solinas once, and he said he didn’t remember what they were. Jerry did seem to wish he remembered, as he could tell it would be useful for people to know exactly how the generation had gone. I think that when they were created, nobody [thought] that the provenance was a big deal.”

Now, Valsorda and other backers have offered a $12,288 bounty for cracking these five hashes – which will be tripled if the recipient chooses to donate it to charity. Half of the sum will go to the person who finds the first seed phrase, and the other half to whoever can find the remaining four.

Valsorda says that finding the hashes won’t weaken elliptic curve cryptography – because it is the nature of the curves that protects data, not the mathematical description of those curves – but that doing so will “help fill in a page of cryptographic history”. He believes that nobody in the 1990s considered that the phrases would be of interest in the future, and that the NSA couldn’t have released them anyway once they discovered that they were jokey phrases about one of their staff wanting a raise.

There are two main ways someone could claim the prize. The first is brute force – simply trying vast numbers of possible seeds, and checking the values created by hashing them against the known curves, which is more feasible than in the 1990s because of advances in computing power. 

But Valsorda says someone may already have the phrases written down. “Some of the people who did this work, or were in the same office as the people who did this work, probably are still around and remember some details,” he says. “The people who are involved in history sometimes don’t realise the importance of what they remember. But I’m not actually suggesting anybody, like, goes stalking NSA analysts.”

Keith Martin at Royal Holloway, University of London, says that the NSA itself would be best-equipped to crack the problem, but probably has other priorities, and anybody else will struggle to find the resources.

“I would be surprised if they’re successful,” he says. “But on the other hand, I can’t say for sure what hardware is out there and what hardware will be devoted to this problem. If someone does find the [phrases], what would be really interesting is how did they do it, rather than that they’ve done it.”

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Matthew Sparkes*

College students learn more calculus in an active learning course in which students solve problems during class than in a traditional lecture-based course. That’s according to a peer-reviewed study my colleagues and I published in science. We also found that college students better understood complex calculus concepts and earned better grades in the active learning course.

The findings held across racial and ethnic groups, genders and college majors, and for both first-time college and transfer students—thus, promoting success for all students. Students in the active learning course had an associated 11% higher pass rate.

If you apply that rate to the current 300,000students taking calculus each year in the U.S., it could mean an additional 33,000 pass their class.

Our experimental trial ran over three semesters—fall 2018 through fall 2019—and involved 811 undergraduate students at a public university that has been designated as a Hispanic-serving institution. The study evaluated the impact of an engagement-focused active learning calculus teaching method by randomly placing students into either a traditional lecture-based class or the active learning calculus class.

The active learning intervention promoted development of calculus understanding during class, with students working through exercises designed to build calculus knowledge and with faculty monitoring and guiding the process.

This differs from the lecture setting where students passively listen to the instructor and develop their understanding outside of class, often on their own.

An active learning approach allows students to work together to solve problems and explain ideas to each other. Active learning is about understanding the “why” behind a subject versus merely trying to memorize it.

Along the way, students experiment with their ideas, learn from their mistakes and ultimately make sense of calculus. In this way, they replicate the practices of mathematicians, including making and testing educated guesses, sense-making and explaining their reasoning to colleagues. Faculty are a critical part of the process. They guide the process through probing questions, demonstrating mathematical strategies, monitoring group progress and adapting pace and activities to foster student learning.

Florida International University made a short video to accompany a research paper on how active learning improves outcomes for calculus students.

Why it matters

Calculus is a foundational discipline for science, technology, engineering and mathematics, as it provides the skills for designing systems as well as for studying and predicting change.

But historically it’s been a barrier that has ended the opportunity for many students to achieve their goal of a STEM career. Only 40% of undergraduate students intending to earn a STEM degree complete their degree, and calculus plays a role in that loss. The reasons vary depending on the student. Failing calculus can be a final straw for some.

And it is particularly concerning for historically underrepresented groups. The odds of female students leaving a STEM major after calculus is 1.5 times higher than it is for men. And Hispanic and Black students have a 50% higher failure rate than white students in calculus. These losses deprive the individual students of STEM aspirations, career dreams and financial security. And it deprives society of their potentially innovative contributions to solving challenging problems, such as climate resilience, energy independence, infrastructure and more.

What still isn’t known

A vexing challenge in calculus instruction—and across the STEM disciplines—is broad adoption of active learning strategies that work. We started this research to provide compelling evidence to show that this model works and to drive further change. The next step is addressing the barriers, including lack of time, questions about effectiveness and institutional policies that don’t provide an incentive for faculty to bring active learning to their classrooms.

A crucial next step is improving the evidence-based instructional change strategies that will promote adoption of active learning instruction in the classroom.

What’s next

Our latest results are motivating our team to further delve into the underlying instructional strategies that drive student understanding in calculus. We’re also looking for opportunities to replicate the experiment at a variety of institutions, including high schools, which will provide more insight into how to expand adoption across the nation.

We hope that this paper increases the rate of change of all faculty adopting active learning in their classrooms.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Laird Kramer, The Conversation

A large team of researchers affiliated with multiple institutions across Europe, has found evidence backing up work by Persi Diaconis in 2007 in which he suggested tossed coins are more likely to land on the same side they started on, rather than on the reverse. The team conducted experiments designed to test the randomness of coin flipping and posted their results on the arXiv preprint server.

For many years, the coin toss (or flip) has represented a fair way to choose between two options—which side of a team goes first, for example, who wins a tied election, or gets to eat the last brownie. Over the years, many people have tested the randomness of coin tossing and most have found it to be as fair as expected—provided a fair coin is used.

But, Diaconis noted, such tests have only tested the likelihood that a fair coin, once flipped, has an equal chance of landing on heads or tails. They have not tested the likelihood of a fair coin landing with the same side up as that when it was flipped. He suggested that due to precession, a coin flipped into the air spends more time there with its initial side facing up, making it more likely to end up that way, as well. He suggested that the difference would be slight, however—just 1%. In this new effort, the research team tested Diaconis’ ideas.

The experiment involved 48 people flipping coins minted in 46 countries (to prevent design bias) for a total of 350,757-coin flips. Each time, the participants noted whether the coin landed with the same side up as when it was launched. The researchers found that Diaconis was right—there was a slight bias. They found the coin landed with the same side up as when it was launched 50.8% of the time. They also found there was some slight variation in percentages between different individuals tossing coins.

The team concludes that while the bias they found is slight, it could be meaningful if multiple coin tosses are used to determine an outcome—for example, flipping a quarter 1,000 times and betting $1 each time (with winnings of 0 or 2$ each round) should result in an average overall win of $19.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Bob Yirka , Phys.org

Researchers Jayne Spiller and Camilla Gilmore at the Center for Mathematical Cognition, University of Loughborough, U.K., have investigated the intersection of sleep and mathematical memory, finding that sleep after learning improves recall.

In their paper, “Positive impact of sleep on recall of multiplication facts,” published in Royal Society Open Science, the duo investigated whether learning complex multiplication problems before sleep would benefit recall compared to learning them during wakefulness to understand how sleep affects the memory of mathematical facts, specifically multiplication tables.

The study involved 77 adult participants aged 18 to 40 from the U.K. Each participant learned complex multiplication problems in two conditions: before sleep (sleep learning) and in the morning (wake learning). Participants completed online sessions where they learned new complex multiplication problems or were tested on previously learned material. Learning sessions included both untimed and timed trials.

Participants had better recall in the sleep learning condition than in the wake learning condition, with a moderate effect size. Even when participants had varying learning abilities, the sleep learning condition showed a beneficial effect on recall, with a smaller effect size.

Mathematical proficiency of the participants, as measured by accuracy in simple multiplication problems, was associated with learning scores but not with the extent of sleep-related benefit for recall.

The study highlights the potential educational implications of leveraging sleep-related benefits for learning. The positive impact of sleep on the recall of complex multiplication problems could be particularly useful for children learning multiplication tables or other math memorization skills, though it would be interesting to see how well a bedtime math lesson would be received.

While the authors suggest that sleep conferred the additional benefit on recall compared with learning during the daytime, the mechanisms by which encoding takes place are possibly enforced by a lack of continued external inputs. The authors point out this limitation of a lack of other comparative stimuli with a similar complexity of encoding to conclusively demonstrate in their study the specificity of sleep-related benefits on recall.

Asleep, the brain may be locking in the new learning because it has no other competition.

In contrast, an awake brain may be confronted with conversations, media reading or viewing and even other classes packed with learning material. This competition for memory encoding in the waking brain could be the cause of the memory differences seen in the study, though outside of recommending multi-hour meditation sessions between classes the likelihood of finding an alternative to sleep on memory may be limited.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to P by Justin Jackson, Phys.org

Like fingerprints, a firearm’s discarded shell casings have unique markings. This allows forensic experts to compare casings from a crime scene with those from a suspect’s gun. Finding and reporting a mismatch can help free the innocent, just as a match can incriminate the guilty.

But a new study from Iowa State University researchers reveals mismatches are more likely than matches to be reported as “inconclusive” in cartridge-case comparisons.

“Firearms experts are failing to report evidence that’s favourable to the defense, and it has to be addressed and corrected. This is a terrible injustice to innocent people who are counting on expert examiners to issue a report showing that their gun was not involved but instead are left defenseless by a report that says the result was inconclusive,” says Gary Wells, an internationally recognized pioneer and scholar in eyewitness memory research.

The Distinguished Professor Emeritus co-authored the paper with Andrew Smith, associate professor of quantitative psychology. Smith studies memory, judgment and decision-making and is affiliated with both the Cognitive Psychology Program and the Psychology and Law Research group at Iowa State.

The two researchers pulled a dataset from a previously published experiment involving 228 firearms examiners and 1,811 cartridge-case comparisons. Overall, the participants were highly accurate in determining whether casings from a common firearm matched or mismatched. But when Smith and Wells applied a well-established mathematical model to the data, they found 32% of actual mismatch trials were reported as inconclusive compared to 1% of actual match trials.

“If the 16% of inconclusive reports lined up more evenly across actual matches and non-matches, we could chalk it up to human error. But the asymmetry, combined with the near-perfect performance of examiners, indicated something else was going on. They almost certainly knew that most of the cases they called inconclusive were actual mismatches,” says Smith.

Asking the wrong question

The researchers say a flawed response scale could help explain the dissociation between what examiners know and what they report.

Currently, the Association of Firearm and Tool Mark Examiners’ Conclusion Scale asks forensic firearms experts whether the crime-scene casings and casings from the suspect’s gun are from the same source. Smith and Wells say the problem with the “source” question is that it’s possible for a mismatch to be attributable to an altered firearm or degraded evidence.

With these possible explanations, Smith and Wells say some examiners might take the position that it is never appropriate to call something a mismatch and instead default to calling the results inconclusive.

“Instead of asking examiners to make source determinations, examiners should simply be asked if the shell casings from the suspect’s gun match the casings found at the crime scene. Asking if the casings match or not and to what degree could provide more transparency,” says Smith.

Questions about alterations and degradation could be asked separately, Smith adds.

Wells emphasizes that until the response scale is fixed, defense lawyers should cross-examine forensic firearms experts who claim inconclusive results. They need to “show their work,” he says. Wells also recommends getting a second opinion if the cartridge-case comparison report comes back as inconclusive.

Bias in the lab

The researchers say another possible explanation for calling a result inconclusive when it’s actually a mismatch is “adversarial allegiance bias.”

“Most forensic firearm examiners and their labs are retained by the prosecution or police departments,” says Smith. “Some examiners might render reports that are inconclusive despite the mismatch because they don’t want to hurt the side that’s essentially their employer.”

Smith and Wells say this type of bias can also occur at the lab level. They point to survey data showing some labs have policies that do not allow examiners to report mismatches.

“It’s hard to get rid of bias but fixing the response scale would go a long way in solving the problem,” says Wells. “In the meantime, there are likely past cases that need relitigated.”

The researchers underscore that forensic science needs to be proficient in not just incriminating the guilty but also in freeing the innocent from suspicion. Minimizing bias and improving transparency in cartridge-case comparisons will help create a more fair and efficient criminal justice system.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Iowa State University

What is a Flipped Classroom?

Most teachers understand the “Chalk and Talk” or “Direct Instruction” method. The teacher begins by reviving what they did the day before, then continue with some new theories and concepts on the board, generally seeking student attention to work through the instances. Then once the maths students have the right set of notes from the board, they would use their textbook for a particular chapter, start solving the questions given by the teacher, and expectantly complete those tasks at home for homework.

As maths tutors, we are familiar that daily practice is significant. However, the students experience problems when practising, and their teacher isn’t there to assist them. The flipped classroom vision reorganizes what comes about at home and school compared to a more conventional plan. In short, the students will first find new content mainly independently, often as homework. Then in class, most of the time burnt out practising, finishing exercises, asking questions, and working on other activities in groups, with the teacher there to guide them.

Why do a Flipped Classroom?

Flipped classrooms permit one-on-one sessions with maths students who are practising, especially for the International Maths Olympiad, so we can move further in more effective directions. Change is challenging, so why do a flipped classroom? In short, change can be strenuous but productive. Bloom’s Two Sigma Problem demonstrates that a one-on-one session is the best method for teaching and learning.

How to Flip Maths Classroom?

Choose a topic to begin with, based on the timing, but you may select a topic that you believe matches the new strategy perfectly.

No matter your standard or plan for the organization, we suggest making a calendar to organize your unit before you begin.

It would be best if you had a simple outline of what lessons or concepts you will cover each day.

If you plan to create your own video sessions, you must figure out the best video recording practices.

Explain to students

If students are used to a specific teaching style and method, changing the pattern can also be an issue for them. It’s necessary to be clear with them about the switch that is taking place, why they’re happening, and what the students should anticipate in the outcome.

This is how one can flip for a maths classroom. Happy teaching!

In a remarkable breakthrough in the field of mathematical science, Professor Kyudong Choi from the Department of Mathematical Sciences at UNIST has provided an irrefutable proof that certain spherical vortices exist in a stable state. This discovery holds significant implications for predicting weather anomalies and advancing weather prediction technologies. The research is published in the journal Communications on Pure and Applied Mathematics.

A vortex is a rotating region of fluid, such as air or water, characterized by intense rotation. Common examples include typhoons and tornadoes frequently observed in news reports. Professor Choi’s mathematical proof establishes the stability of specific types of vortex structures that can be encountered in real-world fluid flows.

The study builds upon the foundational Euler equation formulated by Leonhard Euler in 1757 to describe the flow of eddy currents. In 1894, British mathematician M. Hill mathematically demonstrated that a ball-shaped vortex could maintain its shape indefinitely while moving along its axis.

Professor Choi’s research confirms that Hill’s spherical vortex maximizes kinetic energyunder certain conditions through the application of variational methods. By incorporating functional analysis and partial differential equation theory from mathematical analysis, this study extends previous investigations on two-dimensional fluid flows to encompass three-dimensional fluid dynamics with axial symmetry conditions.

One notable feature identified by Hill is the presence of strong upward airflow at the front of the spherical vortex—an attribute often observed in phenomena like typhoons and tornadoes. Professor Choi’s findings serve as a starting point for further studies involving measurements related to residual time associated with these ascending air currents.

“Research on vortex stability has gained international attention,” stated Professor Choi. “And it holds long-term potential for advancements in today’s weather forecasting technology.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to JooHyeon Heo, Ulsan National Institute of Science and Technology