Month: August 2023

Mathematicians at The University of Manchester have answered the question: How many lottery tickets do you need to buy to guarantee wining something on the U.K. National Lottery?

Focusing on the National Lottery’s flagship game “Lotto,” which draws six random numbersfrom 1 to 59, Dr. David Stewart and Dr. David Cushing found that 27 is the lowest possible number of tickets needed to guarantee a win—although, importantly, with no guarantee of a profit.

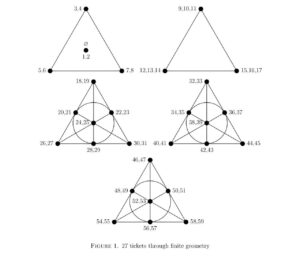
They describe the solution using a mathematical system called finite geometry, which centers around a triangle-like structure called a Fano plane. Each point of the structure is plotted with pairs of numbers and connected with lines—each line generates a set of six numbers, which equates to one ticket.

It takes three Fano planes and two triangles to cover all 59 numbers and generate 27 sets of tickets.

Choosing tickets in this way guarantees that no matter which of the 45,057,474 possible draws occurs, at least one of the tickets will have at least two numbers in common. From any draw of six, two numbers must appear on one of the five geometric structures, which ensures they appear on at least one ticket.

But Dr. Stewart and Dr. Cushing say that the hard work is actually showing that achieving the same outcome with 26 tickets is not possible.

Dr. David Stewart, a Reader in Pure Mathematics at The University of Manchester, said, “Fundamentally there is a tension which comes from the fact that there are only 156 entries on 26 tickets. This means a lot of numbers can’t appear a lot of times. Eventually you see that you’ll be able to find six numbers that don’t appear on any ticket together. In graph theory terms, we end up proving the existence of an independent set of size six.”

Although guaranteed a win, the researchers say that the chances of making a profit are very unlikely and shouldn’t be used as a reason to gamble.

The 27 lottery tickets would set you back £54. And Peter Rowlett, a mathematician from The Aperiodical website, has shown that in almost 99% of cases, you wouldn’t make that money back.

When putting the theory to the test in the lottery draw on 1 July 2023; the researchers matched just two balls on three of the tickets, the reward being three lucky dip tries on a subsequent lottery, each of which came to nothing.

The researchers say that the finding is interesting from a computational point of view. They use a fifty-year-old programming language called Prolog, which they say makes it one of the oldest examples of real artificial intelligence.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to University of Manchester

Buying a specific set of 27 tickets for the UK National Lottery will mathematically guarantee that you win something.

Buying 27 tickets ensures a win in the UK National Lottery

You can guarantee a win in every draw of the UK National Lottery by buying just 27 tickets, say a pair of mathematicians – but you won’t necessarily make a profit.

While there are many variations of lottery in the UK, players in the standard “Lotto” choose six numbers from 1 to 59, paying £2 per ticket. Six numbers are randomly drawn and prizes are awarded for tickets matching two or more.

David Cushing and David Stewart at the University of Manchester, UK, claim that despite there being 45,057,474 combinations of draws, it is possible to guarantee a win with just 27 specific tickets. They say this is the optimal number, as the same can’t be guaranteed with 26.

The proof of their idea relies on a mathematical field called finite geometry and involves placing each of the numbers from 1 to 59 in pairs or triplets on a point within one of five geometrical shapes, then using these to generate lottery tickets based on the lines within the shapes. The five shapes offer 27 such lines, meaning that 27 tickets bought using those numbers, at a cost of £54, will hit every possible winning combination of two numbers.

The 27 tickets that guarantee a win on the UK National Lottery

Their research yielded a specific list of 27 tickets (see above), but they say subsequent work has shown that there are two other combinations of 27 tickets that will also guarantee a win.

“We’ve been thinking about this problem for a few months. I can’t really explain the thought process behind it,” says Cushing. “I was on a train to Manchester and saw this [shape] and that’s the best logical [explanation] I can give.”

Looking at the winning numbers from the 21 June Lotto draw, the pair found their method would have won £1810. But the same numbers played on 1 July would have matched just two balls on three of the tickets – still a technical win, but giving a prize of just three “lucky dip” tries on a subsequent lottery, each of which came to nothing.

Stewart says proving that 27 tickets could guarantee a win was the easiest part of the research, while proving it is impossible to guarantee a win with 26 was far trickier. He estimates that the number of calculations needed to verify that would be 10¹⁶⁵, far more than the number of atoms in the universe. “There’d be absolutely no way to brute force this,” he says.

The solution was a computer programming language called Prolog, developed in France in 1971, which Stewart says is the “hero of the story”. Unlike traditional computer languages where a coder sets out precisely what a machine should do, step by step, Prolog instead takes a list of known facts surrounding a problem and works on its own to deduce whether or not a solution is possible. It takes these facts and builds on them or combines them in order to slowly understand the problem and whittle down the array of possible solutions.

“You end up with very, very elegant-looking programs,” says Stewart. “But they are quite temperamental.”

Cushing says the research shouldn’t be taken as a reason to gamble more, particularly as it doesn’t guarantee a profit, but hopes instead that it encourages other researchers to delve into using Prolog on thorny mathematical problems.

A spokesperson from Camelot, the company that operates the lottery, told New Scientist that the paper made for “interesting reading”.

“Our approach has always been to have lots of people playing a little, with players individually spending small amounts on our games,” they say. “It’s also important to bear in mind that, ultimately, Lotto is a lottery. Like all other National Lottery draw-based games, all of the winning Lotto numbers are chosen at random – any one number has the same and equal chance of being drawn as any other, and every line of numbers entered into a draw has the same and equal chance of winning as any other.”

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Matthew Sparkes*

In addition to describing biological interactions, evolutionary theory has also become a valuable tool to make sense of the dynamics of social norms. Social norms determine which behaviours should be regarded as positive, and how community members should act towards each other.

In a recent publication, published in PLOS Computational Biology, researchers from RIKEN, Japan, and the Max-Planck-Institute for Evolutionary Biology (MPI) describe a new class of social norms for cooperative interactions.

Social norms play an important role in people’s everyday lives. They govern how people should behave and how reputations are formed based on past behaviours.

In the last 25 years, there has been an effort to describe these dynamics of reputations more formally, using mathematical models borrowed from evolutionary game theory. These models describe how social norms evolve over time—how successful norms can spread in a society and how detrimental norms fade.

Most of these models assume that an individual’s reputation should only depend on what this person did in the past. However, everyday experience and experimental evidence suggest that additional external factors may as well influence a person’s reputation. People do not only earn a reputation for how they act, but also based on who they interact with, and how they are affected by those interactions.

For example, with a recent series of experiments, researchers from Harvard University have shown that victims of harmful actions are often regarded as more virtuous than they actually are. To explore such phenomena more formally, researchers at the MPI for Evolutionary Biology in Plön and RIKEN, Japan, have developed a new mathematical framework to describe social norms.

According to the new framework, when a person’s action affects the well-being of another community member, the reputations of both individuals may be updated. Using this general framework, the researchers explore which properties such norms ought have to support cooperative interactions. Surprisingly, some of these social norms indeed have the property observed in the earlier experiments: when one individual defects against another, the victim’s reputation should improve.

Moreover, the researchers also observe a fundamental trade-off. Norms that are particularly good in sustaining cooperation tend to be less robust with respect to noise (such as when reputations are shaped by third-party gossip).

Overall, this work is part of a bigger effort to understand key properties of social norms in a rigorous manner. These studies shed light on which ecological and social environments facilitate cooperation, and on the effects of social norms more generally.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Max Planck Society

In the face of existential dilemmas that are shared by all of humanity, including the consequences of inequality or climate change, it is crucial to understand the conditions leading to cooperation. A new game theory model developed at the Institute of Science and Technology Austria (ISTA) based on 192 stochastic games and on some elegant algebra finds that both cases—available information and the lack thereof—can lead to cooperative outcomes.

The journal Nature Communications has published a new open-access paper on the role information plays in reaching a cooperative outcome. Working at ISTA with the Chatterjee group, research scholar Maria Kleshnina developed a framework of stochastic games, a tool to describe how people make decisions in changing environments. The new model finds that availability of information is intricately linked to cooperative outcomes.

“In this paper, we present a new model of games where a group’s environment changes, based on actions of group members who do not necessarily have all relevant information about their environment. We find that there are rich interactions between the availability of information and cooperative behaviour.

“Counter-intuitively there are instances where there is a benefit of ignorance, and we characterize when information helps in cooperation,” says Professor Krishnendu Chatterjee who leads the “Computer-Aided Verification, Game Theory” group at the Institute of Science and Technology Austria, where this work was done.

Ignorance can be beneficial for cooperation too

In 2016, Štěpán Šimsa, one of the authors of the new paper was working with the Chatterjee group, when he ran some preliminary simulations to find that ignorance about the state of the game may benefit cooperation. This is counter-intuitive since the availability of information is generally thought to be universally beneficial. Christian Hilbe, then a postdoc with the Chatterjee group, along with Kleshnina, thought this to be a worthy research direction. The group then took on the task of investigating how information or the lack thereof affects the evolution of cooperation.

“We quantified in which games it is useful to have precise information about the environmental state. And we find that in most cases, around 80 to 90% it is indeed really good if players are aware of the environment’s state and which game they are playing right now. Yet, we also find some very interesting exceptional cases, where it’s actually optimal for cooperation if everyone is ignorant about the game they are playing,” says co-author Christian Hilbe, who now leads the research group Dynamics of Social Behaviour at the Max Planck Institute for Evolutionary Biology in Germany.

The researchers’ framework represents an idealized model for cooperation in changing environments. Therefore, the results cannot be directly transferred to real-world applications like solving climate change. For this, they say, a more extensive model would be required. Although, from the basic science model that she has built, Kleshnina is able to offer a qualitative direction.

“In a changing system, a benefit of ignorance is more likely to occur in systems that naturally punish non-cooperation. This could happen, for example, if the group’s environment quickly deteriorates if players no longer cooperate mutually. In such a system, individuals have strong incentives to cooperate today, if they want to avoid playing an unprofitable game tomorrow,” she says.

To illustrate the benefit of ignorance, Kleshnina says, “For example, we found that in informed populations, individuals can use their knowledge to employ more nuanced strategies. These nuanced strategies, however, can be less effective in sustaining cooperation. In such a case, there is indeed a small benefit of ignorance towards cooperation.”

A brilliant method

Game theory is, in its essence, a study of mathematical models set up within the framework of games or exchange of logical decisions being played between rational players. Its applications in understanding social and biological evolution have been welcomed by interdisciplinary researchers given its game-changing approach.

Within the context of evolutionary game theory, many models investigate cooperation but most assume that the same game is played over and over again, and also that the players are always perfectly aware of the game that they are playing and its state at any given moment. The new study weakens these general assumptions, first by allowing the simulated players to play different games over time. And second, by accounting for the impact of information.

“The beauty of this approach is that one can combine some elegant linear algebra with extensive computer simulations,” says Kleshnina.

The new framework opens up many new research directions. For instance, what is the role of asymmetric information? One player might know the exact game being played, but another may not. This is not something that the model currently covers. “In that sense, our paper has quite [a few] future applications within theory itself,” Hilbe adds.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Institute of Science and Technology Austria

Everyone knows that 2 + 2 = 4, but why do we have arithmetic in the first place, and why is it true? Researchers at the University of Canterbury have recently answered these questions by “reverse engineering” arithmetic from a psychological perspective. To do this, they considered all possible ways that quantities could be combined, and proved (for the first time in mathematical terms) that addition and multiplication are the simplest.

Their proof is based on four assumptions—principles of perceptual organization—that shape how we and other animals experience the world. These assumptions eliminate all possibilities except arithmetic, like how a sculptor’s work reveals a statue hidden in a block of stone.

Monotonicity is the idea of “things changing in the same direction,” and helps us keep track of our place in the world, so that when we approach an object it looms larger but smaller when we move away. Convexity is grounded in intuitions of betweenness. For example, the four corners of a football pitch define the playing field even without boundary lines connecting them. Continuity describes the smoothness with which objects seem to move in space and time. Isomorphism is the idea of sameness or analogy. It’s what allows us to recognize that a cat is more similar to a dog than it is to a rock.

Taken together, these four principles structure our perception of the world so that our everyday experience is ordered and cognitively manageable.

The implications, explained in a paper in Psychological Review, are far-reaching because arithmetic is fundamental for mathematics and science. They suggest arithmetic is biologically-based and a natural consequence of our perception. Mathematics is thus a realization in symbols of the fundamental nature of the mind, and as such both invented and discovered. The seemingly magical success of mathematics in the physical sciences hints that our mind and the world are not separate, but part of a common unity.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to University of Canterbury