Month: July 2023

You thought the maze looked fun, but now you can’t find your way out. Luckily, mathematics is here to help you escape, says Katie Steckles.

Getting lost in a maze is no fun, and on that rare occasion when you find yourself stuck in one without a map or a bird’s-eye view, it can be difficult to choose which way to go. Mathematics gives us a few tools we can use – in particular, topology, which concerns shapes and how they connect.

The most devious mazes are designed to be as confusing as possible, with dead ends and identical-looking junctions. But there is a stunningly simple rule that will always get you out of a maze, no matter how complicated: always turn right.

Any standard maze can be solved with this method (or its equivalent, the “always-turn-left” method). To do it, place one hand on the wall of the maze as you go in and keep it there. Each time you come to a junction, keep following the wall – if there is an opening on the side you are touching, take it; otherwise go straight. If you hit a dead end, turn around and carry on.

The reason this works is because the walls of any solvable maze will always have at least two distinct connected pieces: one to the left of the optimal solution path (shown in red), and one to the right. The section of wall next to the entrance is part of the same connected chunk of maze as the wall by the exit, and if you keep your hand on it, you will eventually walk along the whole length of the edge of this object – no matter how many twists and turns this involves – and reach the part at the exit.

While it is guaranteed to work, this certainly won’t be the most efficient path – you might find you traverse as much as half of the maze in the process, or even more depending on the layout. But at least it is easy to remember the rule.

Some mazes have more than two pieces. In these, disconnected sections of wall (shown in yellow) inside the maze create loops. In this case, if you start following the wall somewhere in the middle of the maze, there is a chance it could be part of an isolated section, which would leave you walking around a loop forever. But if you start from a wall that is connected to the outside, wall-following will still get you out.

It is reassuring to know that even if you are lost in a maze, you can always get out by following some variation on this rule: if you notice you have reached part of the maze you have been to before, you can detect loops, and switch to the opposite wall.

This is especially useful for mazes where the goal is to get to the centre: if the centre isn’t connected to the outside, wall-following won’t work, and you will need to switch walls to get onto the centre component. But as long as there are a finite number of pieces to the maze, and you keep trying different ones, you will eventually find a piece that is connected to your goal. You might, however, miss the bus home.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Katie Steckles*

Board games based on numbers, like Monopoly, Othello and Chutes and Ladders, make young children better at math, according to a comprehensive review of research published on the topic over the last 23 years.

Board games are already known to enhance learning and development including reading and literacy.

Now this new study, published in the journal Early Years, finds, for 3- to 9-year-olds, the format of number-based board games helps to improve counting, addition, and the ability to recognize if a number is higher or lower than another.

The researchers say children benefit from programs—or interventions—where they play board games a few times a week supervised by a teacher or another trained adult.

“Board games enhance mathematical abilities for young children,” says lead author Dr. Jaime Balladares, from Pontificia Universidad Católica de Chile, in Santiago, Chile.

“Using board games can be considered a strategy with potential effects on basic and complex math skills.

“Board games can easily be adapted to include learning objectives related to mathematical skills or other domains.”

Games where players take turns to move pieces around a board differ from those involving specific skills or gambling.

Board game rules are fixed which limits a player’s activities, and the moves on the board usually determine the overall playing situation.

However, preschools rarely use board games. This study aimed to compile the available evidence of their effects on children.

The researchers set out to investigate the scale of the effects of physical board games in promoting learning in young children.

They based their findings on a review of 19 studies published from 2000 onwards involving children aged from 3 to 9 years. All except one study focused on the relationship between board games and mathematical skills.

All children participating in the studies received special board game sessions which took place on average twice a week for 20 minutes over one-and-a-half months. Teachers, therapists, or parents were among the adults who led these sessions.

In some of the 19 studies, children were grouped into either the number board game or to a board game that did not focus on numeracy skills. In others, all children participated in number board games but were allocated different types (e.g., Dominoes).

All children were assessed on their math performance before and after the intervention sessions which were designed to encourage skills such as counting out loud.

The authors rated success according to four categories including basic numeric competency such as the ability to name numbers, and basic number comprehension (e.g., ‘nine is greater than three’).

The other categories were deepened number comprehension—where a child can accurately add and subtract—and interest in mathematics.

In some cases, parents attended a training session to learn arithmetic that they could then use in the games.

Results showed that math skills improved significantly after the sessions among children for more than half (52%) of the tasks analysed.

In nearly a third (32%) of cases, children in the intervention groups gained better results than those who did not take part in the board game intervention.

The results also show that from analysed studies to date, board games on the language or literacy areas, while implemented, did not include scientific evaluation (i.e. comparing control with intervention groups, or pre and post-intervention) to evaluate their impact on children.

Designing and implementing board games along with scientific procedures to evaluate their efficacy, therefore, are “urgent tasks to develop in the next few years,” Dr. Balladares, who was previously at UCL, argues.

And this, now, is the next project they are investigating.

Dr. Balladares concludes, “Future studies should be designed to explore the effects that these games could have on other cognitive and developmental skills.

“An interesting space for the development of intervention and assessment of board games should open up in the next few years, given the complexity of games and the need to design more and better games for educational purposes.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Taylor & Francis

Putting off college math could improve the likelihood that students remain in college. But that may only be true as long as students don’t procrastinate more than one year. This is what colleagues and I found in a study published in 2023 of 1,119 students at a public university for whom no remedial coursework was required during their first year.

Enrolling in a math course during the first semester of college resulted in students being four times more likely to drop out. Although delayed enrollment in a math course had benefits in the first year, its advantages vanished by the end of the second year. In our study, almost 40% of students who postponed the course beyond a year did not attempt it at all and failed to obtain a degree within six years.

Why it matters

Nearly 1.7 million students who recently graduated from high school will immediately enroll in college. Math is a requirement for most degrees, but students aren’t always ready to do college-level math. By putting off college math for a year, it gives students time to adjust to college and prepare for more challenging coursework.

Approximately 40% of four-year college students must first take a remedial math course. This can extend the time it takes to graduate and increase the likelihood of dropping out. Our study did not apply to students who need remedial math.

For students who do not require remedial courses, some delay can be beneficial, but students’ past experiences in math can lead to avoidance of math courses. Many students experience math anxiety. Procrastination can be an avoidance strategy for managing fears about math. The fear of math for students may be a more significant barrier than their performance.

It is estimated that at least 17% of the population will likely experience high levels of math anxiety. Math anxiety can lead to a drop in math performance. It can also lead to avoiding majors and career paths involving math.

Our study fills the void in research on the effects of how soon students take college-level math courses. It also supports prior evidence that students benefit from a mix of coursework that is challenging yet not overwhelming as they transition to college.

What still isn’t known

We believe colleges need to better promote student confidence in math by examining how student success courses can reduce math anxiety. Student success courses provide students with study skills, note-taking skills, goal setting, time management and stress management, as well as career and financial decision making to support the transition to college. Although student success courses are a proven practice that help students stick with college, rarely do these courses address students’ fear of math.

Students are at the greatest risk of dropping out of college during their first year. Advisors play a crucial role in providing students with resources for success. This includes recommendations on what courses to take and when to take them. More research is also needed about how advisors can effectively communicate the impact of when math is taken by students.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Forrest Lane, The Conversation

Life, from the perspective of thermodynamics, is a system out of equilibrium, resisting tendencies towards increasing their levels of disorder. In such a state, the dynamics are irreversible over time. This link between the tendency toward disorder and irreversibility is expressed as the ‘arrow of time’ by the English physicist Arthur Eddington in 1927.

Now, an international team including researchers from Kyoto University, Hokkaido University, and the Basque Center for Applied Mathematics, has developed a solution for temporal asymmetry, furthering our understanding of the behaviour of biological systems, machine learning, and AI tools.

“The study offers, for the first time, an exact mathematical solution of the temporal asymmetry—also known as entropy production—of nonequilibrium disordered Ising networks,” says co-author Miguel Aguilera of the Basque Center for Applied Mathematics.

The researchers focused on a prototype of large-scale complex networks called the Ising model, a tool used to study recurrently connected neurons. When connections between neurons are symmetric, the Ising model is in a state of equilibrium and presents complex disordered states called spin glasses. The mathematical solution of this state led to the award of the 2021 Nobel Prize in physics to Giorgio Parisi.

Unlike in living systems, however, spin crystals are in equilibrium and their dynamics are time reversible. The researchers instead worked on the time-irreversible Ising dynamics caused by asymmetric connections between neurons.

The exact solutions obtained serve as benchmarks for developing approximate methods for learning artificial neural networks. The development of learning methods used in multiple phases may advance machine learning studies.

“The Ising model underpins recent advances in deep learning and generative artificial neural networks. So, understanding its behaviour offers critical insights into both biological and artificial intelligence in general,” added Hideaki Shimazaki at KyotoU’s Graduate School of Informatics.

“Our findings are the result of an exciting collaboration involving insights from physics, neuroscience and mathematical modeling,” remarked Aguilera. “The multidisciplinary approach has opened the door to novel ways to understand the organization of large-scale complex networks and perhaps decipher the thermodynamic arrow of time.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Kyoto University

Proofs, the central tenet of mathematics, occasionally have errors in them. Could computers stop this from happening, asks mathematician Emily Riehl.

Computer proof assistants can verify that mathematical proofs are correct

One miserable morning in 2017, in the third year of my tenure-track job as a mathematics professor, I woke up to a worrying email. It was from a colleague and he questioned the proof of a key theorem in a highly cited paper I had co-authored. “I had always kind of assumed that this was probably not true in general, though I have no proof either way. Did I miss something?” he asked. The proof, he noted, appeared to rest on a tacit assumption that was not warranted.

Much to my alarm and embarrassment, I realised immediately that my colleague was correct. After an anxious week working to get to the bottom of my mistake, it turned out I was very lucky. The theorem was true; it just needed a new proof, which my co-authors and I supplied in a follow-up paper. But if the theorem had been false, the whole edifice of consequences “proven” using it would have come crashing down.

The essence of mathematics is the concept of proof: a combination of assumed axioms and logical inferences that demonstrate the truth of a mathematical statement. Other mathematicians can then attempt to follow the argument for themselves to identify any holes or convince themselves that the statement is indeed true. Patched up in this way, theorems originally proven by the ancient Greeks about the infinitude of primes or the geometry of planar triangles remain true today – and anyone can see the arguments for why this must be.

Proofs have meant that mathematics has largely avoided the replication crises pervading other sciences, where the results of landmark studies have not held up when the experiments were conducted again. But as my experience shows, mistakes in the literature still occur. Ideally, a false claim, like the one I made, would be caught by the peer review process, where a submitted paper is sent to an expert to “referee”. In practice, however, the peer review process in mathematics is less than perfect – not just because experts can make mistakes themselves, but also because they often do not check every step in a proof.

This is not laziness: theorems at the frontiers of mathematics can be dauntingly technical, so much so that it can take years or even decades to confirm the validity of a proof. The mathematician Vladimir Voevodsky, who received a Fields medal, the discipline’s highest honour, noted that “a technical argument by a trusted author, which is hard to check and looks similar to arguments known to be correct, is hardly ever checked in detail”. After several experiences in which mistakes in his proofs took over a decade to be resolved – a long time for something to sit in logical limbo – Voevodsky’s subsequent crisis of confidence led him to take the unusual step of abandoning his “curiosity-driven research” to develop a computer program that could verify the correctness of his work.

This kind of computer program is known as a proof assistant, though it might be better called a “proof checker”. It can verify that a string of text proves the stated theorem. The proof assistant knows the methods of logical reasoning and is equipped with a library of proofs of standard results. It will accept a proof only after satisfying each step in the reasoning process, with no shortcuts of the sort that human experts often use.

For instance, a computer can verify that there are infinitely many prime numbers by validating the following proof, which is an adaptation of Greek mathematician Euclid’s argument. The human mathematician first tells the computer exactly what is being claimed – in this case that for any natural number N there is always some prime number p that is larger. The human then tells the computer the formula, defining p to be the minimum prime factor of the number formed by multiplying all the natural numbers up to N together and adding 1, represented as N! + 1.

For the computer proof assistant to make sense of this, it needs a library that contains definitions of the basic arithmetic operations. It also needs proofs of theorems, like the fundamental theorem of arithmetic, which tells us that every natural number can be factored uniquely into a product of primes. The proof assistant then demands a proof that this prime number p is greater than N. This is argued by contradiction – a technique where following an assumption to its conclusion leads to something that cannot possibly be true, demonstrating that the original assumption was false. In this case, if p is less than or equal to N, it should be a factor of both N! + 1 and N!. Some simple mathematics says this means that p must also be a factor of 1, which is absurd.

Computer proof assistants can be used to verify proofs that are so long that human referees are unable to check every step. In 1998, for example, Samuel Ferguson and Thomas Hales announced a proof of Johannes Kepler’s 1611 conjecture that the most efficient way to pack spheres into three-dimensional space is the familiar “cannonball” packing. When their result was accepted for publication in 2005 it came with a caveat: the journal’s reviewers attested to “a strong degree of conviction of the essential correctness of this proof approach” – they declined to certify that every step was correct.

Ferguson and Hales’s proof was based on a strategy proposed by László Fejes Tóth in 1953, which reduced the Kepler conjecture to an optimisation problem in a finite number of variables. Ferguson and Hales figured out how to subdivide this optimisation problem into a few thousand cases that could be solved by linear programming, which explains why human referees felt unable to vouch for the correctness of each calculation. In frustration, Hales launched a formalisation project, where a team of mathematicians and computer scientists meticulously verified every logical and computational step in the argument. The resulting 22-author paper was published in 2017 to as much fanfare as the original proof announcement.

Computer proof assistants can also be used to verify results in subfields that are so technical that only specialists understand the meaning of the central concepts. Fields medallist Peter Scholze spent a year working out the proof of a theorem that he wasn’t quite sure he believed and doubted anyone else would have the stamina to check. To be sure that his reasoning was correct before building further mathematics on a shaky foundation, Scholze posed a formalisation challenge in a SaiBlog post entitled the “liquid tensor experiment” in December 2020. The mathematics involved was so cutting edge that it took 60,000 lines of code to formalise the last five lines of the proof – and all the background results that those arguments relied upon – but nevertheless this project was completed and the proof confirmed this past July by a team led by Johan Commelin.

Could computers just write the proofs themselves, without involving any human mathematicians? At present, large language models like ChatGPT can fluently generate mathematical prose and even output it in LaTeX, a typesetting program for mathematical writing. However, the logic of these “proofs” tends to be nonsense. Researchers at Google and elsewhere are looking to pair large language models with automatically generated formalised proofs to guarantee the correctness of the mathematical arguments, though initial efforts are hampered by sparse training sets – libraries of formalised proofs are much smaller than the collective mathematical output. But while machine capabilities are relatively limited today, auto-formalised maths is surely on its way.

In thinking about how the human mathematics community might wish to collaborate with computers in the future, we should return to the question of what a proof is for. It’s never been solely about separating true statements from false ones, but about understanding why the mathematical world is the way it is. While computers will undoubtedly help humans check their work and learn to think more clearly – it’s a much more exacting task to explain mathematics to a computer than it is to explain it to a kindergartener – understanding what to make of it all will always remain a fundamentally human endeavour.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Emily Riehl*

On June 23, 1993, the mathematician Andrew Wiles gave the last of three lectures detailing his solution to Fermat’s last theorem, a problem that had remained unsolved for three and a half centuries. Wiles’ announcement caused a sensation, both within the mathematical community and in the media.

Beyond providing a satisfying resolution to a long-standing problem, Wiles’ work marks an important moment in the establishment of a bridge between two important, but seemingly very different, areas of mathematics.

History demonstrates that many of the greatest breakthroughs in math involve making connections between seemingly disparate branches of the subject. These bridges allow mathematicians, like the two of us, to transport problems from one branch to another and gain access to new tools, techniques and insights.

What is Fermat’s last theorem?

Fermat’s last theorem is similar to the Pythagorean theorem, which states that the sides of any right triangle give a solution to the equation x² + y² = z² .

Every differently sized triangle gives a different solution, and in fact there are infinitely many solutions where all three of x, y and z are whole numbers—the smallest example is x=3, y=4 and z=5.

Fermat’s last theorem is about what happens if the exponent changes to something greater than 2. Are there whole-number solutions to x³ + y³ = z³ ? What if the exponent is 10, or 50, or 30 million? Or, most generally, what about any positive number bigger than 2?

Around the year 1637, Pierre de Fermat claimed that the answer was no, there are no three positive whole numbers that are a solution to xⁿ + yⁿ = zⁿ for any n bigger than 2. The French mathematician scribbled this claim into the margins of his copy of a math textbook from ancient Greece, declaring that he had a marvelous proof that the margin was “too narrow to contain.”

Fermat’s purported proof was never found, and his “last theorem” from the margins, published posthumously by his son, went on to plague mathematicians for centuries.

Searching for a solution

For the next 356 years, no one could find Fermat’s missing proof, but no one could prove him wrong either—not even Homer Simpson. The theorem quickly gained a reputation for being incredibly difficult or even impossible to prove, with thousands of incorrect proofs put forward. The theorem even earned a spot in the Guinness World Records as the “most difficult math problem.”

That is not to say that there was no progress. Fermat himself had proved it for n=3 and n=4. Many other mathematicians, including the trailblazer Sophie Germain, contributed proofs for individual values of n, inspired by Fermat’s methods.

But knowing Fermat’s last theorem is true for certain numbers isn’t enough for mathematicians—we need to know it’s true for infinitely many of them. Mathematicians wanted a proof that would work for all numbers bigger than 2 at once, but for centuries it seemed as though no such proof could be found.

However, toward the end of the 20th century, a growing body of work suggested Fermat’s last theorem should be true. At the heart of this work was something called the modularity conjecture, also known as the Taniyama-Shimura conjecture.

A bridge between two worlds

The modularity conjecture proposed a connection between two seemingly unrelated mathematical objects: elliptic curves and modular forms.

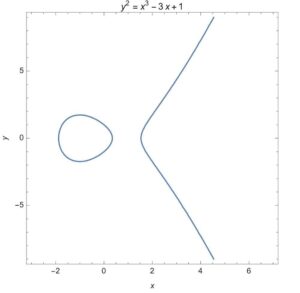
Elliptic curves are neither ellipses nor curves. They are doughnut-shaped spaces of solutions to cubic equations, like y² = x³—3x + 1.

A modular form is a kind of function which takes in certain complex numbers—numbers with two parts: a real part and an imaginary part—and outputs another complex number. What makes these functions special is that they are highly symmetrical, meaning there are lots of conditions on what they can look like.

There is no reason to expect that those two concepts are related, but that is what the modularity conjecture implied.

Finally, a proof

The modularity conjecture doesn’t appear to say anything about equations like xⁿ + yⁿ = zⁿ . But work by mathematicians in the 1980s showed a link between these new ideas and Fermat’s old theorem.

First, in 1985, Gerhard Frey realized that if Fermat was wrong and there could be a solution to xⁿ + yⁿ = zⁿ for some n bigger than 2, that solution would produce a peculiar elliptic curve. Then Kenneth Ribet showed in 1986 that such a curve could not exist in a universe where the modularity conjecture was also true.

Their work implied that if mathematicians could prove the modularity conjecture, then Fermat’s last theorem had to be true. For many mathematicians, including Andrew Wiles, working on the modularity conjecture became a path to proving Fermat’s last theorem.

Wiles worked for seven years, mostly in secret, trying to prove this difficult conjecture. By 1993, he was close to having a proof of a special case of the modularity conjecture—which was all he needed to prove Fermat’s last theorem.

He presented his work in a series of lectures at the Isaac Newton Institute in June 1993. Though subsequent peer review found a gap in Wiles’ proof, Wiles and his former student Richard Taylor worked for another year to fill in that gap and cement Fermat’s last theorem as a mathematical truth.

Lasting consequences

The impacts of Fermat’s last theorem and its solution continue to reverberate through the world of mathematics. In 2001, a group of researchers, including Taylor, gave a full proof of the modularity conjecture in a series of papers that were inspired by Wiles’ work. This completed bridge between elliptic curves and modular forms has been—and will continue to be—foundational to understanding mathematics, even beyond Fermat’s last theorem.

Wiles’ work is cited as beginning “a new era in number theory” and is central to important pieces of modern math, including a widely used encryption technique and a huge research effort known as the Langlands Program that aims to build a bridge between two fundamental areas of mathematics: algebraic number theory and harmonic analysis.

Although Wiles worked mostly in isolation, he ultimately needed help from his peers to identify and fill in the gap in his original proof. Increasingly, mathematics today is a collaborative endeavor, as witnessed by what it took to finish proving the modularity conjecture. The problems are large and complex and often require a variety of expertise.

So, finally, did Fermat really have a proof of his last theorem, as he claimed? Knowing what mathematicians know now, many of us today don’t believe he did. Although Fermat was brilliant, he was sometimes wrong. Mathematicians can accept that he believed he had a proof, but it’s unlikely that his proof would stand up to modern scrutiny.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Maxine Calle and David Bressoud, The Conversation

Dedekind numbers describe the number of ways sets of logical operations can be combined, and are fiendishly difficult to calculate, with only eight known since 1991 – and now mathematicians have calculated the ninth in the series.

The ninth Dedekind number was calculated using the Noctua 2 supercomputer at Paderborn University in Germany

A 42-digit-long number that mathematicians have been hunting for decades, thanks to its sheer difficulty to calculate, has suddenly been found by two separate groups at the same time. This ninth Dedekind number, as it is known, may be the last in the sequence that is feasible to discover.

Dedekind numbers describe the number of ways a set of logical operations can be combined. For sets of just two or three elements, the total number is easy to calculate by hand, but for larger sets it rapidly becomes impossible because the number grows so quickly, at what is known as a double exponential speed.

“You’ve got two to the power two to the power n, as a very rough estimate of the complexity of this system,” says Patrick de Causmaecker at KU Leuven in Belgium. “If you want to find the Dedekind numbers, that is the kind of magnitude of counting that you will have to face.”

The challenge of calculating higher Dedekind numbers has attracted researchers in many disciplines, from pure mathematicians to computer scientists, over the years. “It’s an old, famous problem and, because it’s hard to crack, it’s interesting,” says Christian Jäkel at Dresden University of Technology in Germany.

In 1991, mathematician Doug Wiedemann found the eighth Dedekind number using 200 hours of number crunching on the Cray-2 supercomputer, one of the most powerful machines at the time. No one could do any better, until now.

After working on the problem on and off for six years, Jäkel published his calculation for the ninth Dedekind number in early April. Coincidently, Causmaecker and Lennart van Hirtum, also at KU Leuven, published their work three days later, having produced the same result. Both groups were unaware of one another. “I was shocked, I didn’t know about their work. I thought it would take at least 10 years or whatever to recompute it,” says Jäkel.

The resulting number is 286,386,577,668,298,411,128,469,151,667,598,498,812,366, which is 42 digits long.

Jäkel’s calculation took 28 days on eight graphical processing units (GPUs). To reduce the number of calculations required, he multiplied together elements from the much smaller fifth Dedekind number.

Causmaecker and van Hirtum instead used a processor called a field-programmable gate array (FPGA) for their work. Unlike a CPU or a GPU, these can perform many different kinds of interrelated calculations at the same time. “In an FPGA, everything is always happening all at once,” says van Hirtum. “You can compare it to a car assembly line.”

Like Jäkel, the team used elements from a smaller Dedekind number, in their case the sixth, but this still required 5.5 quadrillion operations and more than four months of computing time using the Noctua 2 supercomputer at Paderborn University, says van Hirtum.

People are divided on whether another Dedekind number will ever be found. “The tenth Dedekind number will be in the realm of 10 to the power of 82, which puts you at the number of atoms in the visible universe, so you can imagine you need something big in technical advancement that also grows exponentially,” says Jakel.

Van Hirtum also thinks the amount of computing power becomes impractical for the next number, requiring trillions more computations which would require capturing the power output of the entire sun. “This jump in complexity remains absolutely astronomical,” he says.

Causmaecker, however, is more positive, as he thinks new ways of calculating could bring that requirement down. “The combination of exponential growth of computing power, and the power of the mathematical algorithms, will go together and maybe in 20 or 30 years we can compute [Dedekind number] 10.”

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Alex Wilkins*

Children do better at math when music is a key part of their lessons, an analysis of almost 50 years of research on the topic has revealed.

It is thought that music can make math more enjoyable, keep students engaged and help many ease fear or anxiety they have about math. Motivation may be increased and pupils may appreciate math more, the peer-reviewed article in Educational Studies details.

Techniques for integrating music into math lessons range from clapping to pieces with different rhythms when learning numbers and fractions, to using math to design musical instruments.

Previous research has shown that children who are better at music also do better at math. But whether teaching music to youngsters actually improves their math has been less clear.

To find out more, Turkish researcher Dr. Ayça Akın, from the Department of Software Engineering, Antalya Belek University, searched academic databases for research on the topic published between 1975 and 2022.

She then combined the results of 55 studies from around the world, involving almost 78,000 young people from kindergarten pupils to university students, to come up with an answer.

Three types of musical intervention were included the meta-analysis: standardized music interventions (typical music lessons, in which children sing and listen to, and compose, music), instrumental musical interventions (lessons in which children learn how to play instruments, either individually or as part of a band) and music-math integrated interventions, in which music is integrated into math lessons.

Students took math tests before and after taking part in the intervention and the change in their scores was compared with that of youngsters who didn’t take part in an intervention.

The use of music, whether in separate lessons or as part of math classes, was associated with greater improvement in math over time.

The integrated lessons had the biggest effect, with around 73% of students who had integrated lessons doing significantly better than youngsters who didn’t have any type of musical intervention.

Some 69% of students who learned how to play instruments and 58% of students who had normal music lessons improved more than pupils with no musical intervention.

The results also indicate that music helps more with learning arithmetic than other types of math and has a bigger impact on younger pupils and those learning more basic mathematical concepts.

Dr. Akin, who carried out the research while at Turkey’s National Ministry of Education and Antalya Belek University, points out that math and music have much in common, such as the use of symbols symmetry. Both subjects also require abstract thought and quantitative reasoning.

Arithmetic may lend itself particularly well to being taught through music because core concepts, such as fractions and ratios, are also fundamental to music. For example, musical notes of different lengths can be represented as fractions and added together to create several bars of music.

Integrated lessons may be especially effective because they allow pupils to build connections between math and music and provide extra opportunities to explore, interpret and understand math.

Plus, if they are more enjoyable than traditional math lessons, any anxiety students feel about math may be eased.

Limitations of the analysis include the relatively small number of studies available for inclusion. This meant it wasn’t possible to look at the effect of factors such as gender, socio-economic status and length of musical instruction on the results.

Dr. Akin, who is now based at Antalya Belek University, concludes that while musical instruction overall has a small to moderate effect on achievement in math, integrated lessons have a large impact.

She adds, “Encouraging mathematics and music teachers to plan lessons together could help ease students’ anxiety about mathematics, while also boosting achievement.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Taylor & Francis

It’s a dilemma that many a regular bettor probably faces often—deciding when to place a sports bet. In a study entitled, “A statistical theory of optimal decision-making in sports betting,” Jacek Dmochowski, Associate Professor in the Grove School of Engineering at The City College of New York, provides the answer. His original finding appears in the journal PLOS One.

“The central finding of the work is that the objective in sports betting is to estimate the median outcome. Importantly, this is not the same as the average outcome,” said Dmochowski, whose expertise includes machine learning, signal processing and brain-computer interfaces. “I approach this from a statistical point-of-view, but also provide some intuitive results with sample data from the NFL that can be digested by those without a background in math.”

To illustrate one of the findings, he presents a hypothetical example. “Assume that Kansas City has played Philadelphia three times previously. Kansas City has won each of those games by margins of 3, 7, and 35 points. They are playing again, and the point spread has been posted as ‘Kansas City -10.’ This means that Kansas City is favoured to win the game by 10 points according to the sportsbooks.”

For a bettor, Dmochowski added, the optimal decision in this scenario is to bet on Philadelphia (+10), even though they have lost the last three games by an average margin of 15 points. The reason is that the median margin of victory in those games was only 7, which is less than the point spread of 10.

He noted that because a bettor’s intuition may sometimes be more linked to an average outcome rather than the median, the utilization of some data, or even better, a model, is strongly encouraged.

On his new findings, Dmochowski said he was surprised that the derived theorems have not been previously presented, although it is possible that sports books and some statistically-minded bettors have understood at least the basic intuitions that are conveyed by the math.

Moreover, other investigators have reported findings that align with what’s in the paper, principally Fabian Wunderlich and Daniel Memmert at the German Sports University of Cologne.

With a Pew Research poll establishing that one in five Americans have placed a sports bet in the last year, Dmochowski’s study should be of interest to many bettors in this growing enterprise.

He had other advice for potential bettors. Firstly, “Avoid betting on matches for which the sports book has produced estimates that are ‘very close’ to the median outcome. In the case of the National Football League, the analysis shows that ‘very close’ is equivalent to the point spread being within one point of the true median.”

“Secondly, understand that the sports books are incredibly skilled at setting the odds. At the same time, they only need to make a small error to allow a profitable bet. So the goal is to seek out those opportunities.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Jay Mwamba, City College of New York

How can you ensure you use the fewest bags when loading your shopping? A dash of maths will help, says Peter Rowlett.

You have heaped your shopping on the supermarket conveyor belt and a friendly member of the checkout staff is scanning it through. Items are coming thick and fast and you would like to get them in as few bags as possible. What is your strategy?

This is an example of an optimisation problem, from an area of maths called operational research. One important question is, what are you trying to optimise? Are you thinking about the weight of the items, or how much space they will take up? Do you guess how many bags you might need and start filling that many, or put everything in one until you need to start another?

We design algorithms to solve packing problems when they come up at a larger scale than your weekly shop, like making better use of warehouse space or fitting boxes into delivery vans. Similar algorithms are used for cutting raw materials with minimal waste and storing data on servers.

Bag-packing algorithms generally involve placing items into a single bag until you get to one that won’t fit because you have hit a maximum weight or size. When necessary, you open a second bag, and each time you reach an item that won’t fit in an existing bag, you start a new one.

If you are filling multiple bags at once, it is likely you will come across an item that could fit in more than one bag. Which do you choose? There is no clear best answer, but different algorithms give different ways to make this decision. We are looking for rules that can be applied without detailed thought. You might have more subtle requirements, like putting two items in the same bag because they go in the same cupboard at home, but here we want the kind of simple rule a computer program can mindlessly apply to get the most efficient outcomes, using the fewest bags, every time.

One algorithm we could employ is called first fit. For each new item, you look through the bags in the order you opened them, placing the item in the first one it fits in. An advantage is that this is quick to implement, but it can overlook options and end up using more bags than needed.

An alternative that often uses fewer bags overall is called worst fit. When faced with a choice, you look through the currently open bags for the one with the most space and place the item there.

These algorithms work more effectively if you handle the objects in decreasing order – packing the largest or heaviest first will usually need fewer bags.

So now you are armed with a secret weapon for packing: the worst-fit decreasing algorithm. The next time you are in the checkout line, load your bulkiest shopping onto the conveyor belt first, and always put items in the bag with the most space available – it might just help you use fewer bags overall.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Peter Rowlett*