Month: April 2022

It should come as no surprise that the first recorded use of the number zero, recently discovered to be made as early as the 3rd or 4th century, happened in India. Mathematics on the Indian subcontinent has a rich history going back over 3,000 years and thrived for centuries before similar advances were made in Europe, with its influence meanwhile spreading to China and the Middle East.

As well as giving us the concept of zero, Indian mathematicians made seminal contributions to the study of trigonometry, algebra, arithmetic and negative numbers among other areas. Perhaps most significantly, the decimal system that we still employ worldwide today was first seen in India.

The number system

As far back as 1200 BC, mathematical knowledge was being written down as part of a large body of knowledge known as the Vedas. In these texts, numbers were commonly expressed as combinations of powers of ten. For example, 365 might be expressed as three hundreds (3×10²), six tens (6×10¹) and five units (5×10⁰), though each power of ten was represented with a name rather than a set of symbols. It is reasonable to believe that this representation using powers of ten played a crucial role in the development of the decimal-place value system in India.

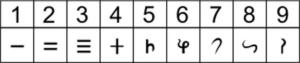
Brahmi numerals. Wikimedia

From the third century BC, we also have written evidence of the Brahmi numerals, the precursors to the modern, Indian or Hindu-Arabic numeral system that most of the world uses today. Once zero was introduced, almost all of the mathematical mechanics would be in place to enable ancient Indians to study higher mathematics.

The concept of zero

Zero itself has a much longer history. The recently dated first recorded zeros, in what is known as the Bakhshali manuscript, were simple placeholders – a tool to distinguish 100 from 10. Similar marks had already been seen in the Babylonian and Mayan cultures in the early centuries AD and arguably in Sumerian mathematics as early as 3000-2000 BC.

But only in India did the placeholder symbol for nothing progress to become a number in its own right. The advent of the concept of zero allowed numbers to be written efficiently and reliably. In turn, this allowed for effective record-keeping that meant important financial calculations could be checked retroactively, ensuring the honest actions of all involved. Zero was a significant step on the route to the democratisation of mathematics.

These accessible mechanical tools for working with mathematical concepts, in combination with a strong and open scholastic and scientific culture, meant that, by around 600AD, all the ingredients were in place for an explosion of mathematical discoveries in India. In comparison, these sorts of tools were not popularised in the West until the early 13th century, though Fibonnacci’s book liber abaci.

Solutions of quadratic equations

In the seventh century, the first written evidence of the rules for working with zero were formalised in the Brahmasputha Siddhanta. In his seminal text, the astronomer Brahmagupta introduced rules for solving quadratic equations (so beloved of secondary school mathematics students) and for computing square roots.

Rules for negative numbers

Brahmagupta also demonstrated rules for working with negative numbers. He referred to positive numbers as fortunes and negative numbers as debts. He wrote down rules that have been interpreted by translators as: “A fortune subtracted from zero is a debt,” and “a debt subtracted from zero is a fortune”.

This latter statement is the same as the rule we learn in school, that if you subtract a negative number, it is the same as adding a positive number. Brahmagupta also knew that “The product of a debt and a fortune is a debt” – a positive number multiplied by a negative is a negative.

For the large part, European mathematicians were reluctant to accept negative numbers as meaningful. Many took the view that negative numbers were absurd. They reasoned that numbers were developed for counting and questioned what you could count with negative numbers. Indian and Chinese mathematicians recognised early on that one answer to this question was debts.

For example, in a primitive farming context, if one farmer owes another farmer 7 cows, then effectively the first farmer has -7 cows. If the first farmer goes out to buy some animals to repay his debt, he has to buy 7 cows and give them to the second farmer in order to bring his cow tally back to 0. From then on, every cow he buys goes to his positive total.

Basis for calculus

This reluctance to adopt negative numbers, and indeed zero, held European mathematics back for many years. Gottfried Wilhelm Leibniz was one of the first Europeans to use zero and the negatives in a systematic way in his development of calculus in the late 17th century. Calculus is used to measure rates of changes and is important in almost every branch of science, notably underpinning many key discoveries in modern physics.

Leibniz: Beaten to it by 500 years.

But Indian mathematician Bhāskara had already discovered many of Leibniz’s ideas over 500 years earlier. Bhāskara, also made major contributions to algebra, arithmetic, geometry and trigonometry. He provided many results, for example on the solutions of certain “Doiphantine” equations, that would not be rediscovered in Europe for centuries.

The Kerala school of astronomy and mathematics, founded by Madhava of Sangamagrama in the 1300s, was responsible for many firsts in mathematics, including the use of mathematical induction and some early calculus-related results. Although no systematic rules for calculus were developed by the Kerala school, its proponents first conceived of many of the results that would later be repeated in Europe including Taylor series expansions, infinitessimals and differentiation.

The leap, made in India, that transformed zero from a simple placeholder to a number in its own right indicates the mathematically enlightened culture that was flourishing on the subcontinent at a time when Europe was stuck in the dark ages. Although its reputation suffers from the Eurocentric bias, the subcontinent has a strong mathematical heritage, which it continues into the 21st century by providing key players at the forefront of every branch of mathematics.

For more insights like this, visit our website at www.international-maths-challenge.com.
Credit of the article given to Christian Yates

The probabilistic revolution first kicked off in the 1600s, when gamblers realized that estimating the likelihood of an event could give them an edge in games of chance.

Today, statistics has become the dominant way to communicate scientific findings. But courts can be hesitant to incorporate statistical evidence into decisions. Indeed, they have historically been antagonistic toward probabilities and are loath to be swindled by slippery statistics.

However, as an educator of statistics who has consulted in a variety of contexts and has served as expert witness to the U.S. District Court in Montana, I find that both my experience and my review of the evidence suggest that courts increasingly feature statistical thinking – whether or not it is identified as such.

Society needs to prioritize educating juries in the language of statistics. Otherwise, juries will be forever at the mercy of convincing, yet potentially invalid, testimony. Courtroom decisions should be based on facts and probabilities, not manipulation by a skilled prosecutor or defense attorney.

Thinking statistically

Probabilities changed the way human beings thought about outcomes. They are a useful tool for expressing our uncertainty about events in the world.

Will it rain today? It will or it will not, that much is certain. But probability allows us to express our ignorance about whether it will rain and quantify the degree to which we are uncertain. Stating “it will probably rain today” constituted a very innovative and different way of thinking.

Probabilities play a role in our daily lives, in decisions from whether to take an umbrella to work to whether to purchase flood insurance. We can consider “statistical thinking” to be any situation where probabilities are involved.

To some extent, humans are intuitive statisticians. For instance, research suggests we can revise a belief in the light of new evidence as prescribed by a statistical theorem, if the probabilities are given in a relatively intuitive rather than abstract fashion.

Statistical reasoning pervades many of the conclusions we draw regarding scientific phenomena. Even physics has had to acknowledge the reality of probabilities. So, if the courts use scientific findings as evidence, probabilities should naturally make their way into courtroom decisions.

Evaluating the evidence

If juries do not understand the nature of statistical conclusions, then they will be tempted to believe that scientific evidence is conclusive and deterministic, rather than probabilistic. For example, probabilities show us that cigarette smoking does not necessarily lead to cancer. Rather, extensive nicotine addiction likely leads to cancer.

Heads or tails? armydre2008/flickr, CC BY

Evidence can only fit a theory probabilistically. If we flip a coin 10 times and get 10 heads in a row, that suggests the coin may not be fair, but does not “prove” that it is biased.

Consider the analysis of DNA found at the crime scene. Is the DNA that of the accused? Maybe. Not definitively. A statistician might say, “The probability of this degree of DNA match occurring by chance is extremely small. The match may be due to chance, but since this probability is so small, we may conclude that it likely did not occur by chance, and use it as evidence against the accused.”

Of course, human judgment is fickle. Until jurors are trained to make rational decisions based on facts and probabilities, they will continue to be easily swayed by convincing litigators.

In the 1995 trial of OJ Simpson, for example, the bloody gloves found at the crime scene constituted powerful evidence against the accused. The samples obtained were extremely likely to belong to the defendant.

A statistically educated jury would not fall for Johnnie Cochran’s classic defense: “If it does not fit, you must acquit.” They would know in advance that no evidence, whatever the kind, fits a theory perfectly.

Cochran’s statement was, statistically speaking, utter nonsense. Of course no model fits perfectly, but which is the more probable model? That’s the task jurors ultimately face, even if they often perceive it as a “guilt” versus “no guilt” decision.

Whenever courts work with DNA matches, they must incorporate acceptable risk and error. But if such uncertainty can be quantified accurately, then it can serve as an aid in decision-making.

Statistical thinking indeed plays a role in the decision between guilt and innocence in a criminal trial. When a jury renders a “guilty” verdict, there is always the chance that the accused is not guilty, but that the many circumstances of the case simply lined up against him or her to lead the jury to a guilty verdict. In other words, the probability of the observed evidence under the assumption of innocence is so low that the evidence likely occurred under a more probable “narrative” – that of guilt.

But, when we make such a decision, we do so with a risk of error. This could be quite devastating to a defendant falsely put to death when all along he or she was innocent. For example, when researchers applied DNA testing to death row inmates in Illinois, they found that the results exonerated several inmates.

Errors in probability-based decisions can indeed be costly. Without a grasp of how virtually all decisions are based on probabilistic thinking, no jury can be expected to adequately assess any evidence in a rational way.

Base rates

Courts also struggle with whether and how to use base rates, another type of statistical tool.

A base rate is the probability of some characteristic being present in the population. For instance, say an individual takes a diagnostic test for a disease, such as HIV. The probability that she has the disease would be higher if she were sampled from a high-risk group – for example, if she shares needles to support a drug addiction, or engages in promiscuous sex with risky partners.

Courts often ignore base rate information. In Stephens v. State in 1989, the Wyoming Supreme Court heard testimony that “80 to 85 percent of child sexual abuse is committed by a close relative of the child.” They ultimately dismissed this, concluding that it was difficult to understand how statistical information would help reach a decision in an individual case.

In another case, a justice of the Minnesota Supreme Court proclaimed that she was “at a loss to understand” how base rates could help predict whether a particular person posed a danger to the public.

Part of the problem is that this information can appear biased against the accused. For instance, consider again the defendant accused of child sexual abuse. The probability that he is guilty might be evaluated in light of the fact that most perpetrators of abuse are relatives of or closely related to the family. This could be interpreted as biasing the evaluation against the accused. However, the courts have considered base rates in employment discrimination cases, an area where perhaps this information seems more naturally relevant (for example, Hazelwood School District v. United States).

If the courts are willing to use base rate information in discrimination cases, they should be encouraged to consider them in other cases as well, even if they seem less intuitive.

Learning to think statistically

Courts should make it a priority to instruct juries on how to interpret probabilistic evidence, so that they are not at the mercy of a convincing, yet potentially misleading, prosecutor or expert witness.

For example, juries might learn elementary statistics through coin-flipping lessons. This could help them, at minimum, find a way to think about the usual “beyond a reasonable doubt” instruction in a criminal trial.

When the assumption of innocence is rejected in favor of guilt, one does so with a risk of being wrong. How much risk is a jury willing to tolerate? Five percent? One percent? Surely such risk must also depend on the severity of the proposed punishment. Every decision is an exercise in risk and cost benefit analysis.

Until juries learn elements of statistical thinking, they are likely to continue making verdict decisions without the appropriate framework in mind. Probabilities have taken over the world, and this fact needs to be recognized by the courts.

For more insights like this, visit our website at www.international-maths-challenge.com.
Credit of the article given to Daniel J. Denis

Credit: Evelyn Lamb

Stacking oranges leads to computer-assisted mathematics. But does it feel like mathematics?

Earlier this month, I attended the Joint Mathematics Meetings in Seattle. One of the reasons I enjoy going to the JMM is that I can get a feel for what is going on in parts of mathematics that I’m not terribly familiar with. This year, I attended two talks in a session called “mathematical information in the digital age,” that got me thinking about what mathematicians do.

First, a confession: I went to the session because I like oranges. The first talk was by Thomas Hales, who is probably best known for his proof of the Kepler conjecture. In short, the conjecture says that the way grocers stack oranges is indeed the most efficient way to do it. The proof was a long case-by-case exhaustion, and Hales was not satisfied with a referee report that said the referee was 99% sure the proof was correct. So he did what any* mathematician would do: he took more than a decade to write and verify a formal computer proof of the result. I attended the talk because I figured there’s a small chance that any talk that mentions the Kepler conjecture might have oranges for the audience.

Hales’ talk was called simply “Formal Proofs.” These are not proofs that are written using stuffy language, with every single step written out, but proofs that can be input into a computer and verified all the way down to the foundations of mathematics, whichever foundations one chooses.

Hales began his talk with some examples of less-than-formal proofs, starting with a passage from William Thurston in which he used the phrase “subdivide and jiggle,” clearly not a rigorous way to describe mathematics. (Incidentally, Thurston also did mathematics with oranges. He would ask students to peel oranges to better understand 2- and 3-dimensional geometry.)

Although I never met Thurston, I am one of his many mathematical descendants. his approach to mathematics, particularly his emphasis on intuition and imagination, has permeated the culture in my extended mathematical family and has had a great deal of influence on how I think about mathematics. That is why it was so refreshing for me to go to a talk where intuition wasn’t a primary focus.

Hales was certainly not insinuating that Thurston was a bad mathematician. Thurston was only the first mathematician he used as an example of less-than-rigorously stated mathematics. A few slides later he mentioned the Bourbaki book on set theory. Yes, even that paragon of formal mathematics sucked dry of every drop of intuition, is not really full of formal proofs.

Hales’ talk was a nice overview of the formal proof programs out there, some mathematical results that have been proved formally (including some that were already known), and a nice introduction to where the field is going. I’m particularly interested in learning more about the QED manifesto and FABSTRACTS, a service that would formalize the abstracts of mathematical papers, a much more tractable goal than formalizing an entire paper.

The most amusing moment of the talk, at least to me, was a question from someone in the audience about the possibility of using a formal proof assistant to verify Mochizuki’s proof of the abc conjecture. Hales replied that with the current technology, you do need to understand the proof as you enter it, so there aren’t many people who can do it. The logical response: why doesn’t Mochizuki do it himself? Let’s just say I’m not holding my breath.

The second talk I attended in the session was Michael Shulman’s called “From the nLab to the HoTT book.” He talked about both the nLab, a wiki for category theory, and the writing of the Homotopy Type Theory “research textbook,” a 600-page tome put together during an IAS semester about homotopy type theory, an alternative to set theory as a foundational system for mathematics. The theme of Shulman’s talk was “one size does not fit all,” either in the way people collaborate (contrasting the wiki and the textbook) or even in the foundations of mathematics (type theory versus set theory).

I don’t know if it was intended, but I thought Shulman’s talk was an interesting counterpoint to Hales,’ most relevantly to me in the way it answered one of the questions Hales posed: why don’t more mathematicians use proof assistants? Beyond the fact that proof assistants are currently too unwieldy for many of us, Shulman’s answer was that we do mathematics for understanding, not just truth. He said what I was thinking during Hales’ talk, which was that to many mathematicians, using a formal proof assistant does not “feel like” mathematics. I am not claiming moral high ground here. It is actually something of a surprise to me that the prospect of being able to find and verify new truths more quickly is not more important to me.

You never know what you’re going to get when you wander into a talk that is well outside your mathematical comfort zone. In my case, I didn’t end up with any oranges, but I got some interesting new-ti-me perspectives about how and why we prove.

*almost no

For more insights like this, visit our website at www.international-maths-challenge.com.

Credit of the article given to Evelyn Lamb