Month: November 2021

Some 20 years ago, my colleague Dr. Chau Tran and I developed a way to simulate the trajectories of millions of basketballs on the computer.

We went to the coaches and assistant coaches at North Carolina State University, where we are based, and told them we had this uncommon ability to study basketball shots very carefully.

Their first question was simple: “What’s the best free throw?” Should the shooter aim towards the front of the hoop or the back? Does it depend on whether the shooter is short or tall?

Math offers a unique perspective. It speeds up the amount of time it takes to see the patterns behind the best shots. For the most part, we discovered things that the players and coaches already knew – but every so often, we came across a new insight.

Simulating millions of shots

From a mathematical viewpoint, basketball is a game of trajectories. These trajectories are unique in that the ball’s motion doesn’t change much when it’s flying through the air, but then rapidly changes over milliseconds when the ball collides with the the hoop or the backboard.

To simulate millions of trajectories without the code taking too long to run, we tried any trick we could think of. We figured out how to go from modestly changing motion to rapidly changing motion, such as when the ball bounces on the rim or off the backboard. We learned how to turn large numbers of trajectories into statistical probabilities. We even created fictitious trajectories in which the ball magically passes through all of the physical obstacles (hoop, backboard, back plate) except for one, to see where it collides first.

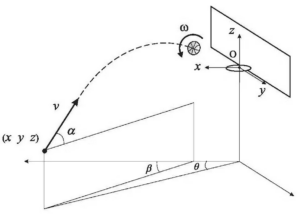
How a mathematician sees a free throw. Larry Silverberg, CC BY-SA

The free throw was the first shot that my colleague and I studied in detail. In close games, teams can win and lose at the free-throw line. What’s more, the free throw is uncontested, so perfection in the free throw can pay off big. Top teams tend to shoot the free shot well.

Our program could tell us what chances the shooter had in sinking a free throw – and help us figure out what he was doing right or wrong.

Breaking down the free throw

We studied the free throw for about five years.

One of the first things we learned from our simulations and by watching TV footage was that players with the same consistency can shoot free throws with anywhere from 75 to 90 percent accuracy. The difference was that the 90 percent players were being consistent at the right shot – the best trajectory.

The fate of a free throw is set the instant the ball leaves the player’s fingertips, so we looked closely at the “launch conditions” of the shot. The ball is located at some height above the floor. It has a rate at which it is spinning backwards (called backspin), and it has a launch speed and a launch angle. Since the shooter never launches the ball the same way, small differences account for a shooter’s consistency.

We found that about 3 hertz of backspin is the best amount; more than that does not help. It takes about 1 second for a ball to reach the basket, so 3 hertz equates to three revolutions in the air, from the instant the ball leaves the player’s hands to when it reaches the basket.

Next, assuming the player releases the ball at 7 feet above the ground, a launch angle of about 52 degrees is best. In that angle, the launch speed is the lowest, and the probability of the shot being successful is the greatest. At 52 degrees, the shooter can be off a degree or more either way without a large effect on the shot’s success.

However, launch speed is quite the opposite. It’s the hardest variable for a player to control. Release the ball too slowly and the shot is short; release it too fast and the shot is long. A player needs to memorize the motion of her entire body during release to impart the same speed consistently.

All else being the same, players who release from higher above the floor have a higher shooting percentage. That’s interesting, because our coaches at N.C. State and others I have talked say that taller players tend to shoot the free throw worse than shorter players do. It seems that the shorter players must try harder.

The last release condition was the most surprising: the aim point of the free throw. We found that the player should aim the ball to the back of the rim. Basically, the back of the rim is more forgiving than the front of the rim. At a release height of 7 feet, the gap between the ball and the back of the ring should be less than 2 inches. A small gap is best whether launching at low or high release heights.

Lessons learned

So what does this all mean for players out there aspiring to improve their free throw?

Our research suggests that players should aim the ball beyond the center of the rim. Launch the ball at a high angle and as high above the ground as possible. (The ball, at the highest point of its arc, should reach the top of the backboard.) Line up the ball to eliminate the side angle. And try to launch the ball with smooth body motion, to produce a consistent launch speed.

In the past few years, we’ve expanded our work to study where the best bank shots strike the backboard and developed a tool for anyone who wants to perfect it.

With tournament play underway, I’m reminded of how competitive the game has become, and how it has truly become a game of inches. As an old basketball player, like many of you, I enjoy watching the game – and, every so often, catching a glimpse of that perfect free throw.

For more insights like this, visit our website at www.international-maths-challenge.com.
Credit of the article given to Larry M. Silverberg

Credit: George Coppock Getty Images

The Lathisms podcast shares the varied stories of Hispanic and Latinx mathematicians

Writer Chimamanda Ngozi Adichie’s popular TED talk is called “The danger of a single story.” In it, she talks about the importance of reading and writing many stories of many people rather than putting a person—or an entire continent of people—into one box. “The single story creates stereotypes,” she says, “and the problem with stereotypes is not that they are untrue but that they are incomplete.”

If someone were asked to tell the story of a “typical” mathematician, they might talk about a shy, socially awkward white man who is a “genius,” whatever that means. He was a fast learner in school and can perform feats of calculation almost instantaneously in his head. He thinks about nothing other than his research, often to the detriment of practical tasks required for everyday living. Some mathematicians do fit these descriptions, but many more don’t. When that story becomes the dominant narrative of who mathematicians are, people who don’t fit the mold feel like there’s no place for them in mathematics. One of the great privileges of working as a math writer is getting to hear the stories of so many mathematicians when I talk to them for articles or podcasts. There really is no one kind of person who becomes a mathematician.

This fall, I’m happy to share a project, created by Lathisms and sponsored by a Tensor-SUMMA grant from the Mathematical Association of America, to share more stories of mathematicians. Lathisms was founded in 2016 by four Hispanic mathematicians, Alexander Diaz-Lopez, Pamela Harris, Alicia Prieto Langarica, and Gabriel Sosa. Hispanic and Latinx people are underrepresented in mathematics, and Lathisms aims to increase visibility of Hispanic and Latinx mathematicians. Since 2016, the organizers have created a calendar every Hispanic Heritage month (September 15-October 15) where each day has a different featured Hispanic or Latinx mathematician, including a picture and short biography of each of them.

This year, Lathisms decided to extend the celebration of Hispanic and Latinx mathematicians by adding a podcast, hosted by me, where you can listen to these mathematicians tell their stories in their own words. Starting at the end of August, we have published a new episode every Friday. The episodes feature mathematicians featured in past years’ Lathisms calendars as well as some of this year’s mathematicians. Some of them grew up in the U.S., others in Latin America. Some grew up in poverty, and others were better off. Some knew they wanted to be mathematicians from a young age, and others didn’t know anything about possible mathematics careers until college. Some work in pure math, others in applied. Some focus on research, others outreach.

So far we’ve shared conversations with Carlos Castillo-Chavez, who is one of the most prolific advisors of U.S. Latinx math Ph.D. students; Erika Camacho, who does mathematical modeling of eye diseases; Federico Ardila, who mentioned “the danger of a single story” when we talked and finds inspiration and mentorship from both students and teachers; and Nicolas Garcia Trillos, who just started a new job in the statistics department at the University of Wisconsin Madison and talked about the many ways there are to be a good mathematician and how that helps him get “unstuck” in his works. In the coming weeks, we will share many more stories. Tune in on Fridays to find them.

You can find the podcast at the Lathisms website or on iTunes. Transcripts are available already for some episodes and will be provided for all episodes. I hope these conversations will be helpful for teachers who want to make sure their students are aware of the diversity of mathematicians, for Hispanic and Latinx students and early-career mathematicians who are looking for role models and collaborators, and for anyone who wants to hear about mathematicians’ many different stories.

For more insights like this, visit our website at www.international-maths-challenge.com.

Credit of the article given to Evelyn Lamb