Month: May 2021

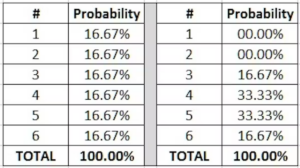
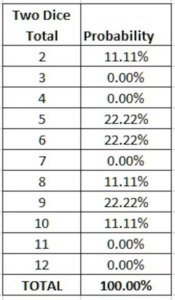
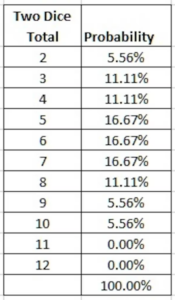
Generally, the occurrence of students asking this question increases with growing age. Primary students know inside out that exams are very important. Brilliant middle school students consider a connection between their test results and semester mark sheets. Ultimately, upon graduation from secondary school, students have comprehended that the totality of their learning has less value than their results in the final exams.

Performance-Oriented Learning

Exam enthusiasm is an indication of performance-oriented learning, and it is intrinsic to our recent education management that needs standards-based reporting of student results. This focuses on performance apart from the method of learning and requests comparison of procurement amongst peers.

The focus for performance-aligned students is showing their capabilities. Fascinatingly, this leads to an affection of fixed mindset characteristics such as the ignorance of challenging tasks because of fear of failure and being intimidated by the success of other students.

Mastery-Oriented Learning

Mastery learning putting down a focus on students developing their competence. Goals are pliably positioned far away from reach, pushing regular growth. The phrase “how can this be even better?” changes the concept of “good enough”. Not to be bewildered with perfectionism, a mastery approach to learning encourages development mindset qualities such as determination, hard work, and facing challenges.

Most forms of mastery learning nowadays can be discovered in the work of Benjamin Bloom in the late 1960s. Bloom saw the important elements of one-to-one teaching that take to effective benefits over group-based classrooms and inspects conveyable instructional plans. Eventually, formative assessment was defined in the circumstances of teaching and learning as a major component for tracking student performance.

So where does mastery learning position in today’s classroom? The idea of formative assessment is frequent, as are posters and discussions encouraging a growth mindset. One significant missing element is making sure that students have a deep knowledge of concepts before moving to the next.

Shifting the Needle

With the growing possibilities offered by Edtech organizations, many are beginning to look to a tech-based solution like International Maths Olympiad Challenge to provide individualized learning possibilities and prepare for the maths Olympiad. The appropriate platform can offer personalized formative assessment and maths learning opportunities.

But we should take a careful viewpoint to utilize technology as a key solution. History shows us that implementing the principles of mastery learning in part restricts potential gains. Despite assessment plans, teachers will also have to promote a mastery-orientated learning approach in their classrooms meticulously. Some strategies are:

• Giving chances for student agency
• Encouraging learning from flaws
• Supporting individual growth with an effective response
• Overlooking comparing students and track performance

We think teaching students how to learn is far more necessary than teaching them what to learn.

Archaeologists recently uncovered a 600-year-old die that was probably used for cheating. The wooden die from medieval Norway has two fives, two fours, a three and a six, while the numbers one and two are missing. It is believed that the die was used to cheat in games, rather than being for a game that requires that specific configuration of numbers.

Today, dice like this with missing numbers are known as tops and bottoms. They can be a useful way to cheat if you’re that way inclined, although they don’t guarantee a win every time and they don’t stand up to scrutiny from suspicious opponents (they only have to ask to take a look and you’ll be found out). But there are several other options of cheating at dice too, and I’ll talk you through some of them here.

It should be noted that using these methods in a casino are illegal and I’m not suggesting you adopt them in such establishments – but it’s an interesting look at how probabilities work.

Probabilities of a fair die and a top and bottom die. Graham Kendall

For a fair die, each number has an equal one in six, or 16.67%, chance of appearing. In the case of the die found in Norway, the numbers four and five are twice as likely to appear (as there are two of them), so have a one in three, or 33.33%, chance. The table shows these probabilities.

It does not take too much imagination to see how tops and bottoms can be used to your advantage. Let’s assume that we are playing with two normal dice. There are 36 possible outcomes but only 11 possible total values the dice can produce. For example, six-four, four-six and five-five all add up to ten.

If we instead used two top and bottom dice with only the numbers one, four and five on them, we can never roll a total of 11 or 12 as we don’t have a six to make that total. Similarly, we can never get a total of three as we don’t have a two and a one. But we also cannot get any combination that would produce a total of seven, which would otherwise be the most likely total to appear with a probability of 16.67%. In a game of craps there are times when it can be really bad to throw a seven. So if you are playing with dice where a combination of seven is impossible, you have a distinct advantage.

As these kind of tops and bottoms dice will not pass even a cursory, closer inspection, they have to be brought into the game for a short time and then switched out again. This requires the cheat to be an expert at palming, meaning being able to conceal one set of dice in your hand and then bring them into play while simultaneously removing the other dice.

Using two dice, with the same three numbers repeated, might be too risky so a cheat would probably only want to switch in a single die into the game. In our example, this would mean no longer avoiding a total of seven, which would still have a probability of 16.67%. But now the totals of five and six would also have this probability.

In craps the odds are such that when you are required to avoid a seven, it is the number most likely to appear. Switching in a single dice can still reduce the house’s chances of winning, by making other totals equally likely to appear.

Loaded dice

Loaded dice can make cheating harder to spot. These can take a number of different forms. For example, some of the spots on one face could be drilled out and the holes filled with a heavy substance so the die is more likely to land with this face down. If you were to drill out the number one, this means that the number six is more likely to appear, as the six is always on the opposite face to the one. Another way of loading a die would be to slightly change its shape, so that it is more likely to keep rolling. This may only give a small advantage, but it could be enough to tip the game in the cheat’s favour.

With tops and bottoms it is easy to know the probabilities of various totals appearing. This is not the case with loaded dice. One way of gauging the probabilities is to toss the dice a number of times (possibly thousands) and work out what numbers appear and how often. If you know that seven is less likely to appear than it would with fair dice then, over the long run, it would be a cheat’s advantage.

Controlled throws

One other way to cheat doesn’t require an unfair die at all but involves learning how to throw in a very controlled way. This can involve effectively sliding or dropping the die so the desired number appears. If two dice are used, one can be used to trap the other and stop it bouncing. If this is done by a skilled operator, it is very difficult to see.

Dominic LoRiggio, the “Dice Dominator”, was able to throw dice in what appeared a normal way but so that they would land on certain numbers. This was done by understanding how dice travel thorough the air and controlling each part of the throw. It took many (many, many) hours of practice to perfect, but he was able to consistently win at the craps table.

Many would consider what LoRiggio did to be advantage play, meaning using the rules to your advantage. This is similar to card counting in blackjack. The casinos may not like it, but you are technically not cheating – though some casino may try to make you shoot the dice in a different way if they suspect you are doing controlled throws.

For more insights like this, visit our website at www.international-maths-challenge.com.
Credit of the article given to Graham Kendall

Credit: Count your pennies! Learn a fun puzzle to test your quick computation skills—and see if you can find new strategies for getting speedy solutions. George Retseck

A puzzling activity from Science Buddies

Introduction
Do you ever use math as a tool to solve interesting problems? In the 1970s math was often taught with simple worksheets. One teacher was looking for a way to help his students have more fun with math and logic. So he developed what is now known as the perimeter magic triangle puzzles. Try them out—and have some fun as you start thinking about counting in a whole new way!

Background
Counting is so common that we forget how it is connected to the broader area of mathematics that studies numbers, known as arithmetic. We can see counting as repeatedly adding one: when you add one object to another you have two objects. Add one more and you have three, and so on. Addition is the process of adding numbers. The result of the addition is called the sum. With smaller numbers you might use counting to find the sum. When you have three and want to add two, for example, you can count two numbers beyond three to get to five. With plenty of practice you can often memorize the sums of the numbers one through 10—at which point in can be fun to play with numbers to find all the ways you can make a particular sum.

Math puzzles and games can be a fun way to get practice working with numbers. Puzzles also provide entertaining ways to build strategic and logical thinking. With a little trial and error you can often start to find new strategies to complete a puzzle faster. These are the very same techniques mathematicians use: starting small and trying to find patterns in the sequence of answers. These patterns are then used to predict the answers to even bigger puzzles.

If this is all too abstract, try the puzzle presented in this activity! It might make the process of learning arithmetic clear.

Materials

• Two sheets of 9 by 12-inch paper, such as construction or craft paper (if possible, choose contrasting colors)
• Pencil or marker
• Ruler
• Scissors
• A quarter or other round object of similar size
• 21 pennies, small blocks or other small stackable objects
• More sheets of paper (optional)

Preparation

• Draw a large triangle on a sheet of paper (you can use a ruler to help make straight lines).
• Use a quarter to trace a circle on each corner of the triangle. Now trace a circle onto the middle of each side of the triangle. You should have six circles.
• On the bottom of the second sheet of paper draw six circles similar in size to the ones drawn on the triangle.
• Cut out these circles, and number them 1 through 6. These circles will be referred to as number disks.
• Keep the top part of the second sheet of paper. You will use it to write down your results.

Procedure

• On the paper with the triangle use the 21 pennies to build towers on each circle. Each circle must have at least 1 penny, but no two towers can be of the same height. Can you do it?
• Keep trying until you find a solution!
• Count the number of pennies in each tower. Write down each sum in order from the smallest to the largest number. What do you notice about this set of numbers?
• Shift the towers around or rebuild them until you can fulfill one more requirement: The total number of pennies used to build the three towers on each side of the triangle must be the same. If you build towers of 1, 5 and 3 pennies in the circles lining up on one side of the triangle, for example, you used 1 + 5 + 3 = 9 pennies on that side. Lining up towers of 1, 2 and 4 pennies on the adjacent side would not work because 1+ 2 + 4 = 7 —not 9 like the first side. (Notice the tower of 1 penny was placed on the corner of this triangle, so it contributes to two sides.) If you tried 1, 2 and 6 for the adjacent side instead, that works because 1 + 2 + 6 = 9. Now you can place the one tower that is left and check if 9 pennies are used in the three towers on the third side of this triangle. Try it out! Did you find a solution?
• If this is not a solution, think. Can you rearrange a few towers and get a solution?
• If working with abstract numbers is easier for you, replace the towers with the number disks. Each number disks then represents a tower of pennies. The number written on the number disks informs you of the number of pennies in that tower.
• Using 9 pennies per side is possible! Did you find the solution? Are there several ways you can arrange the towers so there are 9 pennies used per side?
• Can you arrange the pennies so you use 10, 11 or even 12 pennies per side?
• Extra: Show that there are no solutions that use 8 or fewer pennies per side—or show that there are no solutions with a total of 13 or more pennies per side.
• Extra: The puzzle presented in this activity is called a “perimeter magic triangle of order three.” To extend it to a higher-order perimeter magic triangle start by drawing a new triangle. Add circles on the corners like you did the first time, but this time add two more circles on each side in between the corners. For this puzzle you will need nine number disks. Number them 1 through 9. Just like in the previous puzzle you need to find ways to place the disks on the circles so the sums of the numbers on each side of this triangle are identical. Mathematicians call this triangle a triangle of order four as it has four numbers on each side. Once you have solved this puzzle continue with a triangle of order five (add three more circles between the corners and cut 12 number disks), then order six, and so on.
• Extra: Can you create a strategy to find solutions for this type of puzzle quickly?

Observations and Results
Did you find that you can only arrange the 21 pennies in towers of 1, 2, 3, 4, 5 and 6 pennies if you need to make six towers of different heights? Could you come up with ways to arrange the towers so the sum of pennies used on each side of the triangle is identical for all three sides? It is possible for a total of 9, 10, 11, and 12 pennies per side.

To use a total of 9 pennies on each side, you place the towers with 1, 2, and 3 pennies on the corners of the triangle. The tower of 6 pennies goes in between the towers of 1 and 2 pennies because 1 + 2 + 6 = 9. The tower of 5 pennies stands between the tower of 1 and the tower of 3 pennies, as 1 + 3 + 5 also equals 9. The towers with 2, 4 and 3 pennies fill up the third row. Notice how the smallest towers are placed on the corners for this solution.

To arrange the towers so that you use 12 pennies on each side start by arranging the tallest towers (those with 6, 5 and 4 pennies) on the corners of your triangle and fill in the circles in between. Place the smallest tower you have left (1 penny tall) in between the two tallest towers (5 and 6 pennies each). Do you see that the smallest one you are left with (2 pennies tall) goes in between the tallest ones that need a tower in between (the towers with 6 and 4 pennies each)?

A strategy you could use to find the solution that has 10 pennies on each side is listing all the ways you can make 10 by adding three different numbers. You will find 3 + 2 + 5 = 10, 5 + 4 + 1 = 10, and 1 + 6 + 3 = 10. Can you see that 3, 5 and 1 are part of two of these sums? This means these go on the corners of your triangle. You can use the same strategy to find out how to place the pennies so there are 11 or 12 pennies used on each side.

Are you wondering how you can know that using 8 pennies per side is not possible? With 8 pennies per side you use 3 X  8, or 24, pennies for the triangle. Because you reuse the pennies on the corner towers you at most use 1 + 2 + 3 (the sum of the three smallest towers) or 6 pennies fewer. In other words you can use at most 18 pennies. The puzzle asks you to use 21.

For more insights like this, visit our website at www.international-maths-challenge.com.

Credit of the article given to Science Buddies & Sabine De Brabandere

The central limit theorem – the idea that plotting statistics for a large enough number of samples from a single population will result in a normal distribution – forms the basis of the majority of the inferential statistics that students learn in advanced school-level maths courses. Because of this, it’s a concept not normally encountered until students are much older. In our work on the Framework, however, we always ask ourselves where the ideas that make up a particular concept begin. And are there things we could do earlier in school that will help support those more advanced concepts further down the educational road?

The central limit theorem is an excellent example of just how powerful this way of thinking can be, as the key ideas on which it is built are encountered by students much earlier, and with a little tweaking, they can support deeper conceptual understanding at all stages.

The key underlying concept is that of a sampling distribution, which is a theoretical distribution that arises from taking a very large number of samples from a single population and calculating a statistic – for example, the mean – for each one. There is an immediate problem encountered by students here which relates to the two possible ways in which a sample can be conceptualised. It is common for students to consider a sample as a “mini-population;” this is often known as an additive conception of samples and comes from the common language use of the word, where a free “sample” from a homogeneous block of cheese is effectively identical to the block from which it came. If students have this conception, then a sampling distribution makes no sense as every sample is functionally identical; furthermore, hypothesis tests are problematic as every random sample is equally valid and should give us a similar estimate of any population parameter.

A multiplicative conception of a sample is, therefore, necessary to understand inferential statistics; in this frame, a sample is viewed as one possible outcome from a set of possible but different outcomes. This conception is more closely related to ideas of probability and, in fact, can be built from some simple ideas of combinatorics. In a very real sense, the sampling distribution is actually the sample space of possible samples of size n from a given population. So, how can we establish a multiplicative view of samples early on so that students who do go on to advanced study do not need to reconceptualise what a sample is in order to avoid misconceptions and access the new mathematics?

One possible approach is to begin by exploring a small data set by considering the following:

“Imagine you want to know something about six people, but you only have time to actually ask four of them. How many different combinations of four people are there?”

There are lots of ways to explore this question that make it more concrete – perhaps by giving a list of names of the people along with some characteristics, such as number of siblings, hair colour, method of travel to school, and so on. Early explorations could focus on simply establishing that there are in fact 15 possible samples of size four through a systematic listing and other potentially more creative representations, but then more detailed questions could be asked that focus on the characteristics of the samples; for example, is it common that three of the people in the sample have blonde hair? Is an even split between blue and brown eyes more or less common? How might these things change if a different population of six people was used?

Additionally, there are opportunities to practise procedures within a more interesting framework; for example, if one of the characteristics was height then students could calculate the mean height for each of their samples – a chance to practise the calculation as part of a meaningful activity – and then examine this set of averages. Are they close to a particular value? What range of values are covered? How are these values clustered? Hey presto – we have our first sampling distribution without having to worry about the messy terminology and formal definitions.

In the Cambridge Mathematics Framework, this approach is structured as exploratory work in which students play with the idea of a small sample as a combinatorics problem in order to motivate further exploration. Following this early work, they eventually created their first sampling distribution for a more realistic population and explored its properties such as shape, spread, proportions, etc. This early work lays the ground to look at sampling from some specific population distributions – uniform, normal, and triangular – to get a sense of how the underlying distribution impacts the sampling distribution. Finally, this is brought together by using technology to simulate the sampling distribution for different empirical data sets using varying sizes of samples in order to establish the concept of the central limit theorem.

While sampling distributions and the central limit theorem may well remain the preserve of more advanced mathematics courses, considering how to establish the multiplicative concept of a sample at the very beginning of students’ work on sampling may well help lay more secure foundations for much of the inferential statistics that comes later, and may even support statistical literacy for those who don’t go on to learn more formal statistical techniques.

For more insights like this, visit our website at www.international-maths-challenge.com.

Credit for the article given to Darren Macey