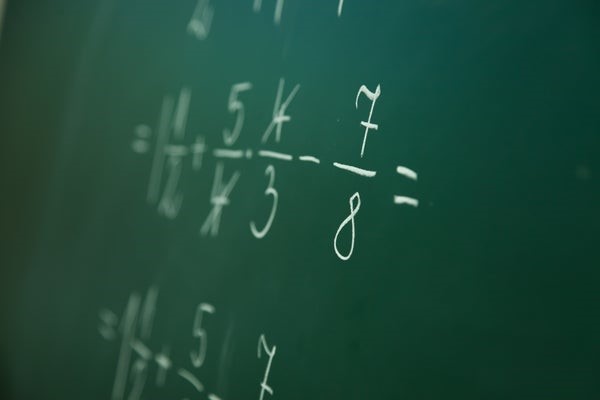Month: July 2020

The first modern electronic digital computer was called the Atanasoff–Berry computer, or ABC.

It was built by physics Professor John Vincent Atanasoff and his graduate student, Clifford Berry, in 1942 at Iowa State College, now known as Iowa State University.

That’s where I have been teaching computer engineering for over 30 years, and I’m also a collector of old computers. I got to meet Atanasoff when he visited Iowa State and got a signed copy of his book.

Before ABC, there were mechanical computing devices that could perform simple calculations. The first mechanical computer, The Babbage Difference Engine, was designed by Charles Babbage in 1822. The ABC was the basis for the modern computer we all use today.

The ABC’s drums. Courtesy of Iowa State University Library Special Collections and University Archives, CC BY-ND

The ABC weighed over 700 pounds and used vacuum tubes. It had a rotating drum, a little bigger than a paint can, that had small capacitors on it. A capacitor is device that can store an electric charge, like a battery.

The ABC was designed to solve problems with up to 29 different variables. You might be familiar with equations with one variable, like 2y = 14. Now imagine 29 different variables. These are common problems in physics and other sciences, but were difficult and time-consuming to solve by hand.

Atanasoff was credited with several breakthrough ideas that are still present in modern computers. The most important idea was using binary digits, just ones and zeroes, to represent all numbers and data. This allowed the calculations to be performed using electronics.

Another idea was the separation of the program (the computer instructions) and memory (places to store numbers).

The ABC completed one operation about every 15 seconds. Compared to the millions of operations per second of today’s computer, that probably seems very slow.

Unlike today’s computers, the ABC did not have a changeable stored program. This meant the program was fixed and designed to do a single task. This also meant that, to solve these problems, an operator had to write down the intermediate answer and then feed that back into the ABC. Atanasoff left Iowa State before he perfected a storage method that would have eliminated the need for the operator to reenter the intermediate results.

Part of the ABC. Courtesy of Iowa State University Library Special Collections and University Archives, CC BY-ND

Shortly after Atanasoff left Iowa State, the ABC was dismantled. Atanasoff never filed a patent for his invention. That means that, for a long time, many people weren’t aware of the ABC.

In 1947, the creators of the Electronic Numerical Integrator And Computer, or ENIAC, filed a patent. This allowed them to claim they were the inventors of the digital computer. For several decades, most people thought that the ENIAC was the first modern computer.

But one of the inventors of the ENIAC had visited Atanasoff in 1941. The courts later ruled that this visit influenced the design of the ENIAC. The ENIAC patent was thrown out by a judge in 1973.

The holders of the ENIAC patent argued that the ABC never really worked. Since all that remained was one of the drum memory units, it was hard to prove otherwise.

In 1997 a team of faculty, researchers and students at Iowa State University finished building a replica of the ABC. They were able to demonstrate that the ABC did function. You can see the replica today at the Computer History Museum in Mountain View, California.

For more insights like this, visit our website at www.international-maths-challenge.com.
Credit of the article given to Doug Jacobson

Credit: Jasmina81 Getty Images

Why do Americans have such trouble with fractions—and what can be done?

Many children never master fractions. When asked whether 12/13 + 7/8 was closest to 1, 2, 19, or 21, only 24% of a nationally representative sample of more than 20,000 US 8th graders answered correctly. This test was given almost 40 years ago, which gave Hugo Lortie-Forgues and me hope that the work of innumerable teachers, mathematics coaches, researchers, and government commissions had made a positive difference. Our hopes were dashed by the data, though; we found that in all of those years, accuracy on the same problem improved only from 24% to 27% correct.

Such difficulties are not limited to fraction estimation problems nor do they end in 8th grade. On standard fraction addition, subtraction, multiplication, and division problems with equal denominators (e.g., 3/5+4/5) and unequal denominators (e.g., 3/5+2/3), 6th and 8th graders tend to answer correctly only about 50% of items. Studies of community college students have revealed similarly poor fraction arithmetic performance. Children in the US do much worse on such problems than their peers in European countries, such as Belgium and Germany, and in Asian countries such as China and Korea.

This weak knowledge is especially unfortunate because fractions are foundational to many more advanced areas of mathematics and science. Fifth graders’ fraction knowledge predicts high school students’ algebra learning and overall math achievement, even after controlling for whole number knowledge, the students’ IQ, and their families’ education and income. On the reference sheets for recent high school AP tests in chemistry and physics, fractions were part of more than half of the formulas. In a recent survey of 2300 white collar, blue collar, and service workers, more than two-thirds indicated that they used fractions in their work. Moreover, in a nationally representative sample of 1,000 Algebra 1 teachers in the US, most rated as “poor” their students’ knowledge of fractions and rated fractions as the second greatest impediment to their students mastering algebra (second only to “word problems”).

Why are fractions so difficult to understand? A major reason is that learning fractions requires overcoming two types of difficulty: inherent and culturally contingent. Inherent sources of difficulty are those that derive from the nature of fractions, ones that confront all learners in all places. One inherent difficulty is the notation used to express fractions. Understanding the relation a/b is more difficult than understanding the simple quantity a, regardless of the culture or time period in which a child lives. Another inherent difficulty involves the complex relations between fraction arithmetic and whole number arithmetic. For example, multiplying fractions involves applying the whole number operation independently to the numerator and the denominator (e.g., 3/7 * 2/7 = (3*2)/(7*7) = 6/49), but doing the same leads to wrong answers on fraction addition (e.g., 3/7 + 2/7 ≠ 5/14). A third inherent source of difficulty is complex conceptual relations among different fraction arithmetic operations, at least using standard algorithms. Why do we need equal denominators to add and subtract fractions but not to multiply and divide them? Why do we invert and multiply to solve fraction division problems, and why do we invert the fraction in the denominator rather than the one in the numerator? These inherent sources of difficulty make understanding fraction arithmetic challenging for all students.

Culturally contingent sources of difficulty, in contrast, can mitigate or exacerbate the inherent challenges of learning fractions. Teacher understanding is one culturally-contingent variable: When asked to explain the meaning of fraction division problems, few US teachers can provide any explanation, whereas the large majority of Chinese teachers provide at least one good explanation. Language is another culturally-contingent factor; East Asian languages express fractions such as 3/4 as “out of four, three,” which makes it easier to understand their meaning than relatively opaque terms such as “three fourth.” A third such variable is textbooks. Despite division being the most difficult operation to understand, US textbooks present far fewer problems with fraction division than fraction multiplication; the opposite is true in Chinese and Korean textbooks. Probably most fundamental are cultural attitudes: Math learning is viewed as crucial throughout East Asia, but US attitudes about its importance are far more variable.

Given the importance of fractions in and out of school, the extensive evidence that many children and adults do not understand them, and the inherent difficulty of the topic, what is to be done? Considering culturally contingent factors points to several potentially useful steps. Inculcating a deeper understanding of fractions among teachers will likely help them to teach more effectively. Explaining the meaning of fractions to students using clear language (for example, explaining that 3/4 means 3 of the 1/4 units), and requesting textbook writers to include more challenging problems are other promising strategies. Addressing inherent sources of difficulty in fraction arithmetic, in particular understanding of fraction magnitudes, can also make a large difference.

Fraction Face-off!, a 12-week program designed by Lynn Fuchs to help children from low-income backgrounds improve their fraction knowledge, seems especially promising. The program teaches children about fraction magnitudes through tasks such as comparing and ordering fraction magnitudes and locating fractions on number lines. After participating in Fraction Face-off!, fourth graders’ fraction addition and subtraction accuracy consistently exceeds of children receiving the standard classroom curriculum. This finding was especially striking because Fraction Face-off! devoted less time to explicit instruction in fraction arithmetic procedures than did the standard curriculum. Similarly encouraging findings have been found for other interventions that emphasize the importance of fraction magnitudes. Such programs may help children learn fraction arithmetic by encouraging them to note that answers such as 1/3+1/2 = 2/5 cannot be right, because the sum is less than one of the numbers being added, and therefore to try procedures that generate more plausible answers. These innovative curricula seem well worth testing on a wider basis.

For more insights like this, visit our website at www.international-maths-challenge.com.

Credit of the article given to Robert S. Siegler