Month: June 2020

Bees are pretty good at maths – as far as insects go, at least. We already know, for example, that they can count up to four and even understand the concept of zero.

But in a new study, published today in the Journal of Experimental Biology, we show honeybees can also understand numbers higher than four – as long as we provide feedback for both correct and incorrect responses as they learn.

Even our own brains are less adept at dealing with numbers greater than four. While we can effortlessly estimate up to four items, processing larger numbers requires more mental effort. Hence why when asked to count, a young child will sometimes answer with “1, 2, 3, 4, more”!

If you don’t believe me, try the test below. The various colour groupings representing 1-4 stars are easy to count quickly and accurately. However, if we try estimating the number of all stars at once by ignoring colours, it requires more concentration, and even then our accuracy tends to be poorer.

For numbers of elements ranging from 1-4, as represented here in different colours, we very efficiently process the exact number. However, if we try estimating the number of all stars at once by ignoring colour, it requires a lot more cognitive effort.

This effect isn’t unique to humans. Fish, for example, also show a threshold for accurate quantity discrimination at four.

One theory to explain this is that counting up to four isn’t really counting at all. It may be that many animals’ brains can innately recognise groups of up to four items, whereas proper counting (the process of sequentially counting the number of objects present) is needed for numbers beyond that.

By comparing the performance of different animal species in various number processing tasks we can better understand how differences in brain size and structure enable number processing. For example, honeybees have previously been shown to be able to count and discriminate numbers up to four, but not beyond. We wanted to know why there was a limit at four – and whether they can go further.

Best bee-haviour

Bees are surprisingly good at maths. We recently discovered that bees can learn to associate particular symbols with particular quantities, much like the way we use numerals to represent numbers.

Bees learn to do this type of difficult task if given a sugary reward for choosing the correct association, and a bitter liquid for choosing incorrectly. So if we were to push bees beyond the four threshold, we knew success would depend on us asking the right question, in the right way, and providing useful feedback to the bees.

We trained two different groups of bees to perform a task in which they were presented with a choice of two different patterns, each containing a different number of shapes. They could earn a reward for choosing the group of four shapes, as opposed to other numbers up to ten.

We used two different training strategies. One group of ten bees received only a reward for a correct choice (choosing a quantity of four), and nothing for an incorrect choice. A second group of 12 bees received a sugary reward for picking four, or a bitter-tasting substance if they made a mistake.

In the test, bees flew into a Y-shaped maze to make a choice, before returning to their hive to share their collected sweet rewards.

Each experiment conducted with a single bee lasted about four hours, by which time each bee had made 50 choices.

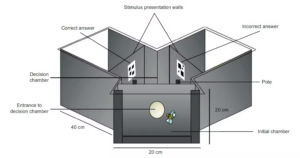
Bees were individually trained and tested in a Y-shaped maze where a sugar reward was presented on the pole directly in front of the correct stimulus. Author provided

The group that only received sweet rewards could not successfully learn to discriminate between four and higher numbers. But the second group reliably discriminated the group of four items from other groups containing higher numbers.

Thus, bees’ ability to learn higher number discrimination depends not just on their innate abilities, but also on the risks and rewards on offer for doing so.

Bee’s-eye view of either four or five element displays that could be discriminated. Inserts show how we normally see these images.

Our results have important implications for understanding how animals’ brains may have evolved to process numbers. Despite being separated by 600 million years of evolution, invertebrates such as bees and vertebrates such as humans and fish all seem to share a common threshold for accurately and quickly processing small numbers. This suggests there may be common principles behind how our brains tackle the question of quantity.

The evidence from our new study shows bees can learn to process higher numbers if the question and training are presented in the right way. These results suggest an incredible flexibility in animal brains, of all sizes, for learning to become maths stars.

For more insights like this, visit our website at www.international-maths-challenge.com.
Credit of the article given to Adrian Dyer, Jair Garcia, Scarlett Howard

Credit: Pavel Bolotov/Thinkstock (MARS)

A rare appearance by enigmatic Shinichi Mochizuki brings faint optimism about his famously impenetrable work

Nearly four years after Shinichi Mochizuki unveiled an imposing set of papers that could revolutionize the theory of numbers, other mathematicians have yet to understand his work or agree on its validity — although they have made modest progress.

Some four dozen mathematicians converged last week for a rare opportunity to hear Mochizuki present his own work at a conference on his home turf, Kyoto University’s Research Institute for Mathematical Sciences (RIMS).

Mochizuki is “less isolated than he was before the process got started”, says Kiran Kedlaya, a number theorist at the University of California, San Diego. Although at first Mochizuki’s papers, which stretch over more than 500 pages, seemed like an impenetrable jungle of formulae, experts have slowly discerned a strategy in the proof that the papers describe, and have been able to zero in on particular passages that seem crucial, he says.

And Jeffrey Lagarias, a number theorist at the University of Michigan in Ann Arbor, says that he got far enough to see that Mochizuki’s work is worth the effort. “It has some revolutionary new ideas,” he says.

Still, Kedlaya says that the more he delves into the proof, the longer he thinks it will take to reach a consensus on whether it is correct. He used to think that the issue would be resolved perhaps by 2017. “Now I’m thinking at least three years from now.”

Others are even less optimistic. “The constructions are generally clear, and many of the arguments could be followed to some extent, but the overarching strategy remains totally elusive for me,” says mathematician Vesselin Dimitrov of Yale University in New Haven, Connecticut. “Add to this the heavy, unprecedentedly indigestible notation: these papers are unlike anything that has ever appeared in the mathematical literature.”

The abc proof

Mochizuki’s theorem aims to prove the important abc conjecture, which dates back to 1985 and relates to prime numbers — whole numbers that cannot be evenly divided by any smaller number except by 1. The conjecture comes in a number of different forms, but explains how the primes that divide two numbers, a and b, are related to those that divide their sum, c.

If Mochizuki’s proof is correct, it would have repercussions across the entire field, says Dimitrov. “When you work in number theory, you cannot ignore the abc conjecture,” he says. “This is why all number theorists eagerly wanted to know about Mochizuki’s approach.” For example, Dimitrov showed in January how, assuming the correctness of Mochizuki’s proof, one might be able to derive many other important results, including a completely independent proof of the celebrated Fermat’s last theorem.

But the purported proof, which Mochizuki first posted on his webpage in August 2012, builds on more than a decade of previous work in which Mochizuki worked in virtual isolation and developed a novel and extremely abstract branch of mathematics.

Mochizuki in the room

The Kyoto workshop followed on the heels of one held last December in Oxford, UK. Mochizuki did not attend that first meeting, although he answered the audience’s questions over a Skype video link. This time, having him in the room — and hearing him present some of the materials himself — was helpful, says Taylor Dupuy, a mathematician at the Hebrew University of Jerusalem who participated in both workshops.

There are now around ten mathematicians who are putting substantial effort into digesting the material — up from just three before the Oxford workshop, says Ivan Fesenko, a mathematician at the University of Nottingham, UK, who co-organized both workshops. The group includes younger researchers, such as Dupuy.

In keeping with his reputation for being a very private person, Mochizuki — who is said to never eat meals in the presence of colleagues — did not take part in the customary mingling and social activities at the Kyoto meeting, according to several sources. And although he was unfailingly forthcoming in answering questions, it was unclear what he thought of the proceedings. “Mochizuki does not give a lot away,” Kedlaya says. “He’s an excellent poker player.”

Fellow mathematicians have criticized Mochizuki for his refusal to travel. After he posted his papers, he turned down multiple offers to spend time abroad and lecture on his ideas. Although he spent much of his youth in the United States, he is now said to rarely leave the Kyoto area. (Mochizuki does not respond to requests for interviews, and the workshop’s website contained the notice: “Activities aimed at interviewing or media coverage of any sort within the facilities of RIMS, Kyoto University, will not be accepted.”)

“He is very level-headed,” says another workshop participant, who did not want to be named. “The only thing that frustrates him is people making rash judgemental comments without understanding any details.”

Still, Dupuy says, “I think he does take a lot of the criticism about him really personally. I’m sure he’s sick of this whole thing, too.”

For more insights like this, visit our website at www.international-maths-challenge.com.

Credit of the article given to Davide Castelvecchi & Nature magazine