Month: April 2020

Grab a few balls and get calculating pi

Pi Day, which occurs every 14 March – or 3/14, in the US date format – celebrates the world’s favourite mathematical constant. This year, why not try an experiment to calculate its value? All you will need is a cardboard tube and a series of balls, each 100 times lighter than the next. You have those lying around the house, right?

This experiment was first formulated by mathematician Gregory Galperin in 2001. It works because of a mathematical trick involving the masses of a pair of balls and the law of conservation of energy.

First, take the tube and place one end up against a wall. Place two balls of equal mass in the tube. Let’s say that the ball closer to the wall is red, and the other is blue.

Next, bounce the blue ball off the red ball. If you have rolled the blue ball hard enough, there should be three collisions: the blue ball hits the red one, the red ball hits the wall, and the red ball bounces back to hit the blue ball once more. Not-so-coincidentally, three is also the first digit of pi.

To calculate pi a little bit more precisely, replace the red ball with one that is 100 times less massive than the blue ball – a ping pong ball might work, so we will call this the white ball.

When you perform the experiment again, you will find that the blue ball hits the white ball, the white ball hits the wall and then the white ball continues to bounce back and forth between the blue ball and the wall as it slows down. If you count the bounces, you’ll find that there are 31 collisions. That gives you the first two digits of pi: 3.1.

Galperin calculated that if you continue the same way, you will keep getting more digits of pi. If you replace the white ball with another one that is 10,000 times less massive than the blue ball, you will find that there are 314 collisions, and so on. If you have enough balls, you can count as many digits of pi as you like.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Leah Crane*

Machines are getting better at maths – artificial intelligence has learned to solve university-level calculus problems in seconds.

François Charton and Guillaume Lample at Facebook AI Research trained an AI on tens of millions of calculus problems randomly generated by a computer. The problems were mathematical expressions that involved integration, a common technique in calculus for finding the area under a curve.

To find solutions, the AI used natural language processing (NLP), a computational tool commonly used to analyse language. This works because the mathematics in each problem can be thought of as a sentence, with variables, normally denoted x, playing the role of nouns and operations, such as finding the square root, playing the role of verbs. The AI then “translates” the problem into a solution.

When the pair tested the AI on 500 calculus problems, it found a solution with an accuracy of 98 per cent. A comparable standard program for solving maths problems had only an accuracy of 85 per cent on the same problems.

The team also gave the AI differential equations to solve, which are other equations that require integration to solve as well as other techniques. For these equations, the AI wasn’t quite as good, solving them correctly 81 per cent for one type of differential equation and 40 per cent on a harder type.

Despite this, it could still correctly answer questions that confounded other maths programs.

Doing calculus on a computer isn’t especially useful in practice, but with further training AI might one day be able to tackle maths problems that are too hard for humans to crack, says Charton.

The efficiency of the AI could save humans time in other mathematical tasks, for example, when proving theorems, says Nikos Aletras at the University of Sheffield, UK.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Gege Li*

The whole is equivalent to the sum of its parts

Which is bigger, 10 or 7?

I suspect that for most, the response to this question is instinctive, unconscious, and immediate. So how about I pose a follow-up question:

How do you know?

If you can refrain from dismissing this question as trivial, I invite you to pause and try to reflect on what happened in your mind in that instant – is this factual recall, was there something visual, was it something contextual, or was it something else?

Perhaps you will indulge me and delve a little deeper:

In how many ways do you know?

Here again, I invite you to pause and consider your response before continuing. Maybe you would like to imagine that you are trying to convince someone or different people. Pick up a piece of paper and draw pictures, write things down, and try to form another approach that is different in some way from the others.

When we compare numerical values, there are many helpful approaches that we can take. These might be based on processes such as: counting, “1, 2, 3, 4, 5, 6, 7, 8, 9, 10. I said 7 first so it must be smaller (that’s how numbers work!)”; motion/movement, “If we start together at the bottom, then I climb 7 stairs and you climb 10 stairs, you will be higher than me (and more tired!)”; measurement/length, “This length (7cm) is shorter than this length (10cm)”; matching/creating correspondences, “There are 10 people and 7 cupcakes if I hand out a cupcake to each person I will run out – not everyone will get one!”

Each of these approaches (and the many more you might imagine) might be grounded in two prominent types of reasoning: part-whole and/or correspondence. These two ideas are used pervasively, interchangeably, and often simultaneously when reasoning with numbers in most of school mathematics and in our daily experiences.

Part-whole

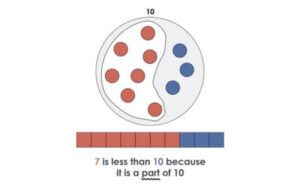
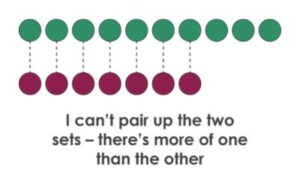
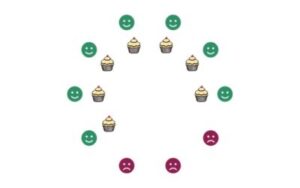
Let’s take another comparison problem, this time inspired by questions posed to children in a study by Falk (2010):

What are there more of:

1. Hairs on your head OR fingers on two hands?
2. Fingers on two hands OR days in a month?
3. Grains of sand on Earth OR hairs on your head?
4. All numbers OR grains of sand on Earth?

This time, I suspect, your responses were not always instantaneous and more conscious thought was required. How convinced are you of your responses? Did you feel as though more information was required?

When you reflect on the reasoning you employed in making these comparisons, I wonder whether you assigned numerical values to the quantities – did you feel an urge to do so, as a first step, before applying similar techniques to those used before?

When the children in this study were faced with such comparisons, an interesting misconception revealed itself: many of them considered a very large number, for instance, the number of grains of sand on Earth, to be synonymous with infinity. This, of course, presents a potential difficulty with question 4; I suspect you won’t be alone if you encounter this, too.

When we encounter numbers or quantities that are so large/vast that they are beyond our comprehension, it is perhaps unsurprising that we equate these with infinity – that magical word that creeps into our consciousness from a very young age as the default answer to any questions about “biggest number.” So, is this a problematic concept to hold? In practical terms, for most people, probably not. But mathematically it is, and actually confronting it offers some wonderful opportunities to explore, discuss and better understand the numbers that we work with, the structure of mathematical systems, and the nature of the mathematics that we study.

So how could we confront this misconception? How can we take advantage of the opportunities alluded to above? Well, one possibility is purposefully to create situations where the misconception might arise.

Position the quantities representing the grains of sand on Earth and all numbers on a number line.

• Would they be in the same place, or would one be closer to zero than the other?
• If they are not in the same place, are they very close together or very far apart?
• Is it possible to measure the gap between these two quantities?

Talking around this task is likely to draw attention to the fact that some quantities may be large and unknown, but we can be certain they are finite – a single number exists to represent them, we just don’t know what it is. Others, however, are large, unknown, and also not finite – they are not represented by a single large number but are unbounded, often the result of an infinite process such as counting. These infinite quantities cannot be positioned on a number line, and the gap (the difference) between any finite quantity and an infinite one is immeasurable – it is infinitely large in itself!

So, is it possible to make comparisons with infinite quantities? Or is this “not allowed?!” Well, we can certainly say that any finite quantity is smaller than any infinite quantity. But how about this:

What are there more of: natural numbers or even numbers?

I would encourage you, once again, to establish and hold your own response to this question in your mind before reading on.

As at the beginning of this blog, the follow-up question is:

How do you know?

Intuition tends to be strong here, grounded in our experiences with finite quantities and part-whole reasoning: the even numbers are a part of the natural numbers so there must be more natural numbers (twice as many, we might argue). We can confirm this with examples; for instance, by comparing the number of natural numbers and even numbers there are up to a fixed point, say 100:

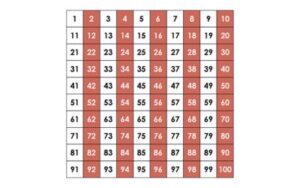
Now, what if I asked you to find an alternative approach, another way of explaining how you know that there are more natural numbers than even numbers? When we compared 7 and 10, we discussed two main approaches, those based on part-whole reasoning and those based on matching / correspondences. What would a correspondence approach look like here?

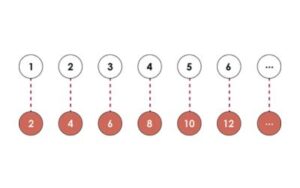
It looks as though I can pair up the two sets of numbers, I can match every natural number, one-to-one, with an even number, so the two sets are equal… Uh oh! And, more than that, our two methods of comparison, which are usually used interchangeably, lead to different results!

How do you feel about this seemingly contradictory situation? Maybe this example is something you are comfortable with, but most likely not! For many students, and indeed teachers, this is a troubling situation, causing us to throw up our hands in despair and confusion! However, if we can overcome this sensation and recognise that the conflict is real (it’s not that we’ve made an error), then the stage is set for thinking more carefully about assumptions that might have been made and when and where our mathematical rules and procedures are used and valid. Giving students similar opportunities to encounter situations where their intuition is called into question, inviting them to discuss (and argue!), expose their own lines of reasoning, and compare contexts and situations in the search for an explanation, is surely a good thing! Perhaps, when prompted in this way they might also be more receptive to the introduction of standard, accepted approaches within mathematics.

As a closing comment, let’s notice that our discussions are touching on the most fundamental property of any infinite set: that it can be matched, one-to-one, with a proper subset of itself. In other words, in the case of infinite sets, the whole is equivalent to some of its parts!

For more insights like this, visit our website at www.international-maths-challenge.com.

Credit for the article given to Tabitha Gould

AI can search through numbers and equations to find patterns

Artificial intelligence’s ability to sift through large amounts of data is helping us tackle one of the most difficult unsolved problems in mathematics.

Yang-Hui He at City, University of London, and his colleagues are using the help of machine learning to better understand the Birch and Swinnerton-Dyer conjecture. This is one of the seven fiendishly difficult Millennium Prize Problems, each of which has a $1 million reward on offer for the first correct solution.

The conjecture describes solutions to equations known as elliptic curves, equations in the form of y² = x³ + ax + b, where x and y are variables and a and b are fixed constants.

Elliptic curves were essential in cracking the long-standing Fermat’s last theorem, which was solved by mathematician Andrew Wiles in the 1990s, and are also used in cryptography.

To study the behaviour of elliptic curves, mathematicians also use an equation called the L-series. The conjecture, first stated by mathematicians Bryan Birch and Peter Swinnerton-Dyer in the 1960s, says that if an elliptic curve has an infinite number of solutions, its L-series should equal 0 at certain points.

“It turns out to be a very, very difficult problem to find a set of integer solutions on such equations,” says He, meaning solutions only involving whole numbers. “This is part of the biggest problem in number theory: how do you find integer solutions to polynomials?”

Finding integer solutions or showing that they cannot exist has been crucial. “For example, Fermat’s last theorem is reduced completely to the statement of whether you can find certain properties of elliptic curves,” says He.

He and his colleagues used an AI to analyse close to 2.5 million elliptic curves that had been compiled in a database by John Cremona at the University of Warwick, UK. The rationale was to search the equations to see if any statistical patterns emerged.

Plugging different values into the elliptic curve equation and plotting the results on a graph, the team found that the distribution takes the shape of a cross, which mathematicians hadn’t previously observed. “The distribution of elliptic curves seems to be symmetric from left to right, and up and down,” says He.

“If you spot any interesting patterns, then you can raise a conjecture which may later lead to an important result,” says He.  “We now have a new, really powerful thing, which is machine learning and AI, to do this.”

To see whether a theoretical explanation exists for the cross-shaped distribution, He consulted number theorists. “Apparently, nobody knows,” says He.

“Machine learning hasn’t yet been applied very much to problems in pure maths,” says Andrew Booker at the University of Bristol, UK. “Elliptic curves are a natural place to start.”

“Birch and Swinnerton-Dyer made their conjecture based on patterns that they observed in numerical data in the 1960s, and I could imagine applications of machine learning that tried to detect those patterns efficiently,” says Booker, but the approach so far is too simple to turn up any deep patterns, he says.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Donna Lu*

Third time’s a charm: just weeks after cracking an elusive problem involving the number 42, mathematicians have found a solution to an even harder problem for the number 3.

Andrew Booker at Bristol University, UK, and Andrew Sutherland at the Massachusetts Institute of Technology have found a big solution to a maths problem known as the sum of three cubes.

The problem asks whether any integer, or whole number, can be represented as the sum of three cubed numbers.

There were already two known solutions for the number 3, both of which involve small numbers: 1³ + 1³ + 1³ and 4³ + 4³ + (-5)³.

But mathematicians have been searching for a third for decades. The solution that Booker and Sutherland found is:

569936821221962380720³ + (-569936821113563493509) ³ + (-472715493453327032) ³ = 3

Earlier this month, the pair also found a solution to the same problem for 42, which was the last remaining unsolved number less than 100.

To find these solutions, Booker and Sutherland worked with software firm Charity Engine to run an algorithm across the idle computers of half a million volunteers.

For the number 3, the amount of processing time was equivalent to a single computer processor running continuously for 4 million hours, or more than 456 years.

When a number can be expressed as the sum of three cubes, there are infinitely many possible solutions, says Booker. “So there should be infinitely many solutions for three, and we’ve just found the third one,” he says.

There’s a reason the third solution for 3 was so hard to find. “If you look at just the solutions for any one number, they look random,” he says. “We think that if you could get your hands on loads and loads of solutions – of course, that’s not possible, just because the numbers get so huge so quickly – but if you could, there’s kind of a general trend to them: that the digit sizes are growing roughly linearly with the number of solutions you find.”

It turns out that this rate of growth is extremely small for the number 3 – only 114, now the smallest unsolved number, has a smaller rate of growth. In other words, numbers with a slow rate of growth have fewer solutions with a lower number of digits.

The duo also found a solution to the problem for 906. We know for sure that certain numbers, such as 4, 5 and 13, can’t be expressed as the sum of three cubes. There now remain nine unsolved numbers under 1000. Mathematicians think these can be written as the sum of three cubes, but we don’t yet know how.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Donna Lu*