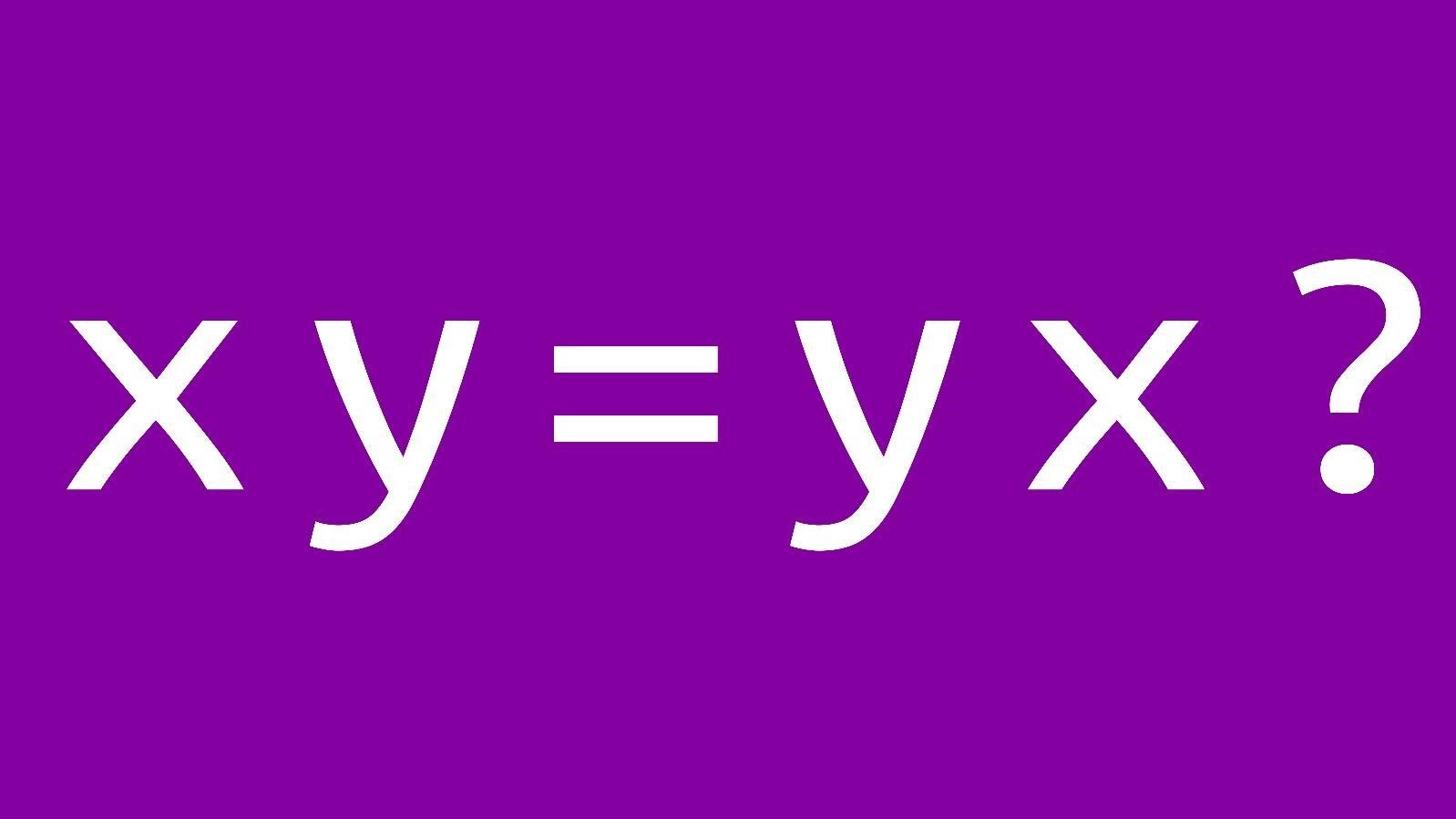Month: July 2019

In any area of math, it’s always good idea to keep a few counterexamples in your back pocket. Examples/non-examples from some of the different subsets of integral domains.

Z[i√5]Z[i5] is an integral domain which is not a UFD

That Z[i√5]Z[i5] an integral domain is easy to check (just computation).

• It’s not a UFD since we can write 6=2⋅3=(1+i√5)(1−i√5)6=2⋅3=(1+i5)(1−i5) as two distinct facorizations into irreducibles*

‍Z[x]Z[x] is a UFD which is not a PID

We know Z[x]Z[x] is a UFD because ZZ is a UFD (recall, a commutative ring RR is a UFD iff R[x]R[x] is a UFD).

• The ideal (2,x)={2f(x)+xg(x):f(x),g(x)∈Z[x]}(2,x)={2f(x)+xg(x):f(x),g(x)∈Z[x]} (polynomials with even constant term) is not principal**

‍Z[12+i√192]Z[12+i192] is a PID which is not a Euclidean domain

• This is a PID since it has a Dedekind-Hasse norm (see Dummit and Foote, 3rd ed., §8.2§8.2).
• It is not a Euclidean domain since it has no universal side divisors (ibid.).

ZZ is a Euclidean domain which is not a field

ZZ is a Euclidean domain via the absolute value norm (which gives the familiar division algorithm).

• It is not a field since the only elements which are units are 11 and −1−1.

‍  (*) Check 2,3,1+i√52,3,1+i5, and 1−i√51−i5 are indeed irreducible in Z[i√5]Z[i5]:

Write 2=αβ2=αβ for α,β∈Z[i√5]α,β∈Z[i5]. Then α=a+ib√5α=a+ib5 and N(α)=a2+5b2N(α)=a2+5b2 for some integers a,ba,b. Since 4=N(2)=N(α)N(β)4=N(2)=N(α)N(β), we must have a2+5b2=1,2a2+5b2=1,2 or 44. Notice b=0b=0 must be true (since a2+5b2∉{1,2,4}a2+5b2∉{1,2,4} for b≥1b≥1 and for any aa). Hence either α=a=1α=a=1 or 22. If α=1α=1 then αα is a unit. If α=2α=2, then we must have β=1β=1 and so ββ is a unit.

• Showing 3 is irreducible follows a similar argument.

‍Write 1+i√5=αβ1+i5=αβ with α=a+ib√5α=a+ib5 so that N(α)=a2+5b2∈{1,2,3,6}N(α)=a2+5b2∈{1,2,3,6} since 6=N(α)N(β)6=N(α)N(β). Consider two cases:  (case 1) If b=0b=0, then a2∈{1,2,3,6}a2∈{1,2,3,6} which is only true if a2=1a2=1 and so α=a=±1α=a=±1 is a unit. (case 2) If b>0b>0, we can only have b2=1b2=1 (since b2>1b2>1 gives a contradiction), and so a2+5∈{1,2,3,6}a2+5∈{1,2,3,6}, which implies a2=1a2=1. Hence α=±1±i√5α=±1±i5 and so N(α)=6N(α)=6. This implies N(β)=1N(β)=1 and so β=±1β=±1, which is a unit.

‍Showing 1−i√51−i5 is irreducible follows a similar argument.

principal in Z[x]Z[x]:

• Suppose to the contrary (2,x)=(f(x))(2,x)=(f(x)) for some polynomial f(x)∈Z[x]f(x)∈Z[x]. Since 2∈(f(x))2∈(f(x)), we must have 2=f(x)p(x)2=f(x)p(x) for some p(x)∈Z[x]p(x)∈Z[x]. Hence 0=degf(x)+degp(x)0=deg⁡f(x)+deg⁡p(x) which implies both f(x)f(x) and p(x)p(x) are constants. In particular, since 2=±1⋅±22=±1⋅±2, we need f(x),p(x)∈{±1,±2}f(x),p(x)∈{±1,±2}. If f(x)=±1f(x)=±1, then (f(x))=Z[x](f(x))=Z[x] which is a contradiction since (f(x))=(2,x)(f(x))=(2,x) mustbe a proper ideal (not every polynomial over Z[x]Z[x] has even constant term). It follows that f(x)=±2f(x)=±2. But since x∈(f(x))x∈(f(x)) as well, x=2r(x)x=2r(x) for some r(x)∈Z[x]r(x)∈Z[x]. But of course this is impossible for any polynomial with integer coefficients, r(x)r(x). Thus (2,x)(2,x) is not principal.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*

Here is a list of some of the subsets of integral domains, along with the reasoning (a.k.a proofs) of why the bullseye below looks the way it does. Part 2 of this post will include back-pocket examples/non-examples of each.

Integral Domain: a commutative ring with 1 where the product of any two nonzero elements is always nonzero

Unique Factorization Domain (UFD): an integral domain where every nonzero element (which is not a unit) has a unique factorization into irreducibles

Principal Ideal Domain (PID): an integral domain where every ideal is generated by exactly one element

Euclidean Domain: an integral domain RR with a norm NN and a division algorithm (i.e. there is a norm NN so that for every a,b∈Ra,b∈R with b≠0b≠0, there are q,r∈Rq,r∈R so that a=bq+ra=bq+r with r=0r=0 or N(r)<N(b)N(r)<N(b))

Field: a commutative ring where every nonzero element has an inverse

Because… We can just choose the zero norm: N(r)=0N(r)=0 for all r∈Fr∈F.

Proof: Let FF be a field and define a norm NN so that N(r)=0N(r)=0 for all r∈Fr∈F. Then for any a,b∈Fa,b∈F with b≠0b≠0, we can writea=b(b−1a)+0.a=b(b−1a)+0.

Because… If I◃RI◃R is an arbitrary nonzero ideal in the Euclidean domain RR, then I=(d)I=(d), where d∈Id∈I such that dd has the smallest norm among all elements in II. Prove this using the division algorithm on dd and some a∈Ia∈I.

Proof: Let RR be a Euclidean domain with respect to the norm NN and let I◃RI◃R be an ideal. If I=(0)I=(0), then II is principle. Otherwise let d∈Id∈I be a nonzero element such that dd has the smallest norm among all elements in II. We claim I=(d)I=(d). That (d)⊂I(d)⊂I is clear so let a∈Ia∈I. Then by the division algorithm, there exist q,r∈Rq,r∈R so that a=dq+ra=dq+r with r=0r=0 or N(r)<N(d)N(r)<N(d). Then r=a−dq∈Ir=a−dq∈I since a,d∈Ia,d∈I. But my minimality of dd, this implies r=0r=0. Hence a=dq∈(d)a=dq∈(d) and so I⊂(d)I⊂(d).

Because…Every PID has the ascending chain condition (acc) on its ideals!* So to prove PID ⇒⇒ UFD, just recall that an integral domain RR is a UFD if and only if 1) it has the acc on principal ideals** and 2) every irreducible element is also prime.

Proof: Let RR be a PID. Then 1) RR has the ascending chain condition on principal ideals and 2) every irreducible element is also a prime element. Hence RR is a UFD.

Because… By definition.

Proof: By definition.

‍*Def: In general, an integral domain RR has the acc on its principal ideals if these two equivalent conditions are satisfied:

1. Every sequence I1⊂I2⊂⋯⊂⋯I1⊂I2⊂⋯⊂⋯ of principal ideals is stationary (i.e. there is an integer n0≥1n0≥1 such that In=In0In=In0 for all n≥n0n≥n0).
2. For every nonempty subset X⊂RX⊂R, there is an element m∈Xm∈X such that whenever a∈Xa∈X and (m)⊂(a)(m)⊂(a), then (m)=(a)(m)=(a).

**To see this, use part 1 of the definition above. If I1⊂I2⊂⋯I1⊂I2⊂⋯ is an acsending chain, consider their union I=⋃∞n=1InI=⋃n=1∞In. That guy must be a principal ideal (check!), say I=(m)I=(m). This implies that mm must live in some In0In0  for some n0≥1n0≥1 and so I=(m)⊂In0I=(m)⊂In0. But since II is the union, we have for all n≥n0n≥n0(m)=I⊃In⊃In0=(m).(m)=I⊃In⊃In0=(m).Voila!

Every field FF is a PID

because the only ideals in a field are (0)(0) and F=(1)F=(1)! And every field is vacuously a UFD since all elements are units. (Recall, RR is a UFD if every non-zero, non-invertible element (an element which is not a unit) has a unique factorzation into irreducibles).

‍In an integral domain, every maximal ideal is also a prime ideal. 

(Proof: Let RR be an integral domain and M◃RM◃R a maximal ideal. Then R/MR/M is a field and hence an integral domain, which implies M◃RM◃R is a prime ideal.)

Butut the converse is not true (see counterexample below). However, the converse is true in a PID because of the added structure!

(Proof: Let RR be a PID and (p)◃R(p)◃R a prime ideal for some p∈Rp∈R. Then pp is a prime – and hence an irreducible – element (prime ⇔⇔ irreducible in PIDs). Since in an integral domain a principal ideal is maximal whenever it is generated by an irreducible element, we conclude (p)(p) is maximal.)

This suggests that if you want to find a counterexample – an integral domain with a prime ideal which is not maximal – try to think of a ring which is not a PID:   In Z[x]Z[x], consider the ideal (p)(p) for a prime integer pp. Then (p)(p) is a prime ideal, yet it is not maximal since(p)⊂(p,x)⊂Z[x].(p)⊂(p,x)⊂Z[x].

‍If FF is a field, then F[x]F[x] – the ring of polynomials in xx with coefficients in FF – is a Euclidean domain with the norm N(p(x))=degp(x)N(p(x))=deg⁡p(x) where p(x)∈F[x]p(x)∈F[x].

By the integral domain hierarchy above, this implies every ideal in F[x]F[x] is of the form (p(x))(p(x)) (i.e. F[x]F[x] is a PID) and every polynomial can be factored uniquely into a product of prime polynomials (just like the integers)! The next bullet gives an “almost converse” statement.

‍If R[x]R[x] is a PID, the RR must be a field.

To see this, simply observe that R⊂R[x]R⊂R[x] and so RR must be an integral domain (since a subset of a integral domain inherets commutativity and the “no zero divisors” property). Since R[x]/(x)≅RR[x]/(x)≅R, it follows that R[x]/(x)R[x]/(x) is also an integral domain. This proves that (x)(x) is a prime ideal. But prime implies maximal in a PID! So R[x]/(x)R[x]/(x) – and therefore RR – is actually a field.

• This is how we know, for example, that Z[x]Z[x] is not a PID (in the counterexample a few bullets up) – ZZ is not a field!

‍For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*

After some exposure to group theory, you quickly learn that when trying to prove a group GG is abelian, checking if xy=yxxy=yx for arbitrary x,yx,y in GG is not always the most efficient – or helpful! – tactic. Here is a (not comprehensive) running tab of other ways you may be able to prove your group is abelian:

Show the commutator [x,y]=xyx−1y−1[x,y]=xyx−1y−1of two arbitary elements x,y∈Gx,y∈G must be the identity

• Show the group is isomorphic to a direct product of two abelian (sub)groups
• Check if the group has order p2p2 for any prime pp OR if the order is pqpq for primes p≤qp≤q with p∤q−1p∤q−1.
• Show the group is cyclic.
• Show |Z(G)|=|G|.|Z(G)|=|G|.
• Prove G/Z(G)G/Z(G) is cyclic. (e.g. does G/Z(G)G/Z(G) have prime order?)
• Show that GG has a trivial commutator subgroup, i.e. is [G,G]={e}[G,G]={e}.

Here’s a thought map which is (probably) more fun than practical. Note, pp and qq denote primes below:

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*

Yes! I’m writing about math. No! Don’t close your browser window. Hear me out first…

I know very well that math has a bad rap. It’s often taught or thought of as a dry, intimidating, unapproachable, completely boring, who-in-their-right-mind-would-want-to-think-about-this-on-purpose kind of subject. I get it. Math was the last thing on earth I thought I’d study. Seriously.

But my understanding of math has since changed. I used to think it was a mess of equations and formulas, only enjoyed by a small number of masochists. But oh how I was wrong! Mathematics is not just numbers. It is not just strange symbols. And it is certainly not something reserved only for the few elite geniuses of the world.

Mathematics is a language –

a language of ideas, concepts, and notions.

‍

It’s true! Math is a language just like English, French, or Mandarin. And just like some ideas are best communicated in a particular language, other ideas are best communicated “in math.” This is why I’ve started a SaiBlog – as an aid in my own pursuit of becoming more proficient at thinking/speaking/reading mathematics.

One of the main challenges I face in this pursuit is the ability to strip away the intimidation factor

– the cryptic symbols, the elaborate vocabulary, the fancy formalities –

and unveil the true meaning of the text at hand. For me, this unveiling comes by reading and rereading, by working through problem after problem, and by writing. Quite often while learning new (and recalling old) mathematics, I have to stop and ask, “What is the text really saying behind all that jargon?” And if I can proceed to write down the idea in English (i.e. in lingo that’s easy on the brain) then that bit of information becomes engrained in my mind. Or at least it gets stored away in my brain somewhere. And if (or when) I forget it, I find that looking at my own handwritten notes conjures up the memory and the blood, sweat, and tears that went into learning that bit of info, and it all comes right back.

So Math3ma is my online repository as I make my way through this journey. Here’s the plan for now: some of the SaiBlog posts will be divided into two sections, in keeping with the aforementioned thought process:

And some posts will fall into “The Back Pocket” where I’ll keep little tidbits of math for a rainy day (or, perhaps, an exam). As for the actual content, I’m focusing on material found in the initial years of a graduate math program because, well, passing the qualifying exams is next on my agenda. But I think I’ll include some include undergrad material too. And as for future content, who knows? I’m excited to see what Math3ma can turn into.

Thanks for taking the time to peak into my journey as I work to see mathematics for what it really is–a very powerful, very beautiful language inherent in the world all around us!

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Tai-Danae Bradley*