Month: March 2019

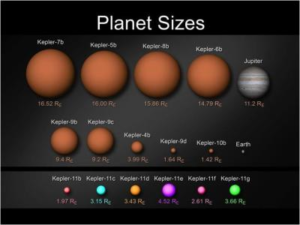
This is a sample from a Spacemath@NASA problem. This diagram shows disks representing the planets discovered in orbit around eight different stars all drawn to the same scale. Earth and Jupiter are also shown for size comparison. This lesson asks the viewer to solve problems using fraction arithmetic to find out how big these new planets are compared to Earth and Jupiter.

NASA today announced that Houghton Mifflin Harcourt (HMH), Boston, has incorporated math problems developed by the SpaceMath@NASA program into some of its latest curriculum and educational products. SpaceMath uses the latest discoveries from NASA’s space science missions to develop grade-appropriate math problems spanning all of the contemporary mathematics topics areas in formal education.

“We are proud of the partnership with HMH, especially at a time when a vibrant, national science, engineering, technology, and math (STEM) education program is a major priority,” said astronomer Sten Odenwald of ADNET Systems, Inc., Lanham, Md. “SpaceMath@NASA has partnered with a major STEM education solutions provider to help students see the deep connections between math and science using NASA and space exploration as a theme.” Odenwald, who is stationed at NASA’s Goddard Space Flight Center in Greenbelt, Md., leads a team of education and public outreach (E&PO) professionals who develop the SpaceMath materials.

“Other education companies are welcome to work with SpaceMath and follow HMH’s example,” says Odenwald. “The informal partnership entails periodic consultation with the company to understand its interests and what types of content best suits its goals. We then build modules on the SpaceMath@NASA website that contain as many content requests as we can accommodate. In turn, we can offer our NASA-version of these modules for open access by all visiting teachers, while HMH is free to download those module elements to populate their own Web pages and books.”

SpaceMath products, simple one-page problems featuring a NASA discovery or engineering issue, are designed for direct classroom use by students in grades 3 through 12 using authentic, on-grade-level math topics rooted in real-world science and engineering data. It was developed in 2003 to help NASA missions upgrade their E&PO offerings by explicitly integrating mathematics problems into the science content. It was also specifically designed to meet the needs of the No Child Left Behind classroom environment where short, targeted math problems in a one-page format were now becoming the preferred method for presenting a variety of math experiences.

Problems are commonly extracted from NASA press releases and written to feature some surprising but quantifiable aspect of an image or discovery that can be paraphrased as simple mathematical problems. “These can be as diverse as a problem on fractions and percentages using Kepler exoplanet data, or as involved as determining the volume of Comet Hartley-2 using integral calculus,” said Odenwald.

“We are very excited to partner with NASA,” said Jim O’Neill, Senior Vice President, Portfolio Strategy and Marketing Management for HMH. “By incorporating the resources provided by SpaceMath@NASA into our programs, HMH can help develop students’ critical thinking skills through real-world applications that are taken from the headlines. These STEM activities also highlight the pedagogy of the Common Core for Mathematics by strengthening students’ abilities to apply concepts and integrate the Standards for Mathematical Practice.”

“Our partnership with HMH has grown out of a 10-year collaboration with them, so we consider them a major partner for future resource development,” adds Odenwald.

SpaceMath was originally funded by NASA’s E&PO programs for the IMAGE and Hinode missions. Since 2008, the program has been funded by two grants from the NASA Science Mission Directorate at NASA Headquarters, Washington – through the Research Opportunities in Space and Earth Sciences/Education and Public Outreach for Earth and Space Science (ROSES/EPOESS) program.

“Funding at the Directorate level has been crucial in allowing SpaceMath to utilize all of NASA’s press releases and extensive resources as subject matter for mathematics problems, rather than focusing exclusively on only a few NASA missions and science themes,” said Odenwald.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to NASA’s Goddard Space Flight Center

Could different jury sizes improve the quality of justice? The answers are not clear, but mathematicians are analysing juries to identify potential improvements.

The U.S. Constitution does not say that juries in criminal cases must include 12 people or that their decisions must be unanimous. In fact, some states use juries of different sizes.

One primary reason why today’s juries tend to have 12 people is that the Welsh king Morgan of Gla-Morgan, who established jury trials in 725 A.D., decided upon the number, linking the judge and jury to Jesus and his Twelve Apostles.

The Supreme Court has ruled that smaller juries can be permitted. States such as Florida, Connecticut and others have used — or considered — smaller juries of six or nine people. In Louisiana, super-majority verdicts of nine jurors out of 12 are allowed.

However, in 1978, the Supreme Court ruled that a five-person jury is not allowed after Georgia attempted to assign five-person juries to certain criminal trials.

To mathematicians and statisticians, this offers a clear division between acceptable and not acceptable, and therefore an opportunity for analysis.

“What seems to be apparent reading the literature on this is that the Supreme Court is making these decisions basically on an intuitive basis,” said Jeff Suzuki, a mathematician at Brooklyn College in New York. “It’s their sense of how big a jury should be to ensure proper deliberation.”

At a mathematics conference earlier this year, Suzuki presented research comparing the likelihood of conviction of a hypothetical defendant with the same likelihood of guilt but different jury conditions.

Building on a well-established line of research, which began with 18th-century French philosopher and mathematician Nicolas de Condorcet, mathematical analysis of juries has continued over the years, beginning from Condorcet’s idea that each juror has some probability of coming to the correct conclusion about the defendant’s guilt or innocence.

Suzuki used three different probabilities to calculate the likely decision of a jury, including the probability that the defendant is actually guilty, the probability that a juror will make the correct decision if the defendant is guilty, and the probability that a juror will make the correct decision if the defendant is not guilty

Suzuki’s model suggests that smaller juries are more likely than larger juries to convict when the defendant appears less certain to be guilty. All the juries he modeled are very likely to convict when the evidence suggests that a defendant is almost certainly guilty. But for slightly less certain cases, differences become clear.

If it appears that there’s an 80 percent likelihood that the defendant is guilty, then Suzuki’s model suggests that less than 10 percent of the time a 12-person jury would unanimously vote to convict, but a 6-person jury would unanimously vote to convict over 25 percent of the time — and a Louisiana-style jury that can convict with nine out of 12 votes would convict in roughly 60 percent of such trials.

Suzuki admits that the models may not be capturing the complete picture. Even if states that use fewer than 12 jurors had higher conviction rates than other states, that wouldn’t mean smaller juries convict greater numbers of innocent defendants, he said.

One potential problem with translating this research to real world trials is that it leaves out the interaction between jurors, which Suzuki admitted is a problem.

“We don’t have a good model for how jurors interact with each other,” he said. “The real challenge is that the data doesn’t really exist.”

In addition to the issue of juror interaction, the [Suzuki’s] models leave out other factors important to finding the correct verdict, such as the possibility that testimony or evidence could deceive the jury, said Bruce Spencer, a professor of statistics at Northwestern University in Evanston, Ill., who did not work with Suzuki.

“If the evidence is very misleading, it’s going to tend to mislead all of [the jurors],” said Spencer.

In a separate study, Spencer analysed surveys completed by judges just before juries delivered their verdict and compared what the judges thought to the juries’ decisions, finding that the verdicts agreed about 80 percent of the time. He found that in about one in every five trials in his study sample, the judge and the jury came to different conclusions.

Real data on the true guilt or innocence of a defendant on trial is simply not available. The jury’s decision is only half the story of a verdict’s accuracy. Many factors in jury decisions cannot be captured quantitatively.

“If you’re coming up with a measure of the speed of light or a standard kilogram, you like to have some assessment of uncertainty,” said Spencer. “I think it is difficult to assess the uncertainty of our estimates.”

Although Spencer knows either the judge or jury must have been wrong in the 20 percent of cases in his study when the two disagreed, there was not enough information to know which was correct in a given case. Using statistical modeling, he found that overall the judges and juries were about equally accurate, but cautioned about drawing conclusions based on the limited number of cases in his study.

Suzuki is trying to figure out more about verdict accuracy with his research. He said that he can build estimates of false conviction rates by counting how many verdicts are later overturned. The estimates are imperfect, he said, especially given that new technology such as DNA testing was not available when some of the original verdicts were given.

But Suzuki feels that his research can at least examine some of the important details of jury trials. Making better models helps to draw general conclusions, despite the uniqueness of each trial.

“You can use probabilistic methods to model human behaviour, provided that you understand what the statistics are and are not telling you, ”Said Suzuki.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Chris Gorski, Inside Science News Service

Alexei Borodin

For anyone who has ever taken a commercial flight, it’s an all-too-familiar scene: Hundreds of passengers sit around waiting for boarding to begin, then rush to be at the front of the line as soon as it does.

Boarding an aircraft can be a frustrating experience, with passengers often wondering if they will ever make it to their seats. But Alexei Borodin, a professor of mathematics at MIT, can predict how long it will take for you to board an airplane, no matter how long the line. That’s because Borodin studies difficult probability problems, using sophisticated mathematical tools to extract precise information from seemingly random groups.

“Imagine an airplane in which each row has one seat, and there are 100 seats,” Borodin says. “People line up in random order to fill the plane, and each person has a carry-on suitcase in their hand, which it takes them one minute to put into the overhead compartment.”

If the passengers all board the plane in an orderly fashion, starting from the rear seats and working their way forwards, it would be a very quick process, Borodin says. But in reality, people queue up in a random order, significantly slowing things down.

So how long would it take to board the aircraft? “It’s not an easy problem to solve, but it is possible,” Borodin says. “It turns out that it is approximately equal to twice the square root of the number of people in the queue.” So with a 100-seat airplane, boarding would take 20 minutes, he says.

Borodin says he has enjoyed solving these kinds of tricky problems since he was a child growing up in the former Soviet Union. Born in the industrial city of Donetsk in eastern Ukraine, Borodin regularly took part in mathematical Olympiads in his home state. Held all over the world, these Olympiads set unusual problems for children to solve, requiring them to come up with imaginative solutions while working against the clock.

It is perhaps no surprise that Borodin had an interest in math from an early age: His father, Mikhail Borodin, is a professor of mathematics at Donetsk State University. “He was heavily involved in research while I was growing up,” Borodin says. “I guess children always look up to their parents, and it gave me an understanding that mathematics could be an occupation.”

In 1992, Borodin moved to Russia to study at Moscow State University. The dissolution of the USSR meant that, arriving in Moscow, Borodin found himself faced with a choice of whether to take Ukrainian citizenship, like his parents back in Donetsk, or Russian. It was a difficult decision, but for practical reasons Borodin opted for Russian citizenship.

Times were tough while Borodin was studying in Moscow. Politically there was a great deal of unrest in the city, including a coup attempt in 1993. Many scientists began leaving Russia, in search of a more stable life elsewhere.

Financially things were not easy for Borodin either, as he had just $15 each month to spend on food and accommodation. “But I still remember the times fondly,” he says. “I didn’t pay much attention to politics at the time, I was working too hard. And I had my friends, and my $15 per month to live on.”

After Borodin graduated from Moscow State University in 1997, a former adviser who had moved to the United States invited Borodin over to join him. So he began splitting his time between Moscow and Philadelphia, where he studied for his PhD at the University of Pennsylvania.

He then spent seven years at the California Institute of Technology before moving to MIT in 2010, where he has continued his research into probabilities in large random objects.

Borodin says there are no big mathematical problems he is desperate to solve. Instead, his greatest motivation is the pursuit of what he calls the beauty of the subject. While it may seem strange to talk about finding beauty in abstract mathematical constructions, many mathematicians view their work as an artistic endeavor.

“If one asks 100 mathematicians to describe this beauty, one is likely to get 100 different answers,” he says.

And yet all mathematicians tend to agree that something is beautiful when they see it, he adds, saying, “It is this search for new instances of mathematical beauty that largely drives my research.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Helen Knight, Massachusetts Institute of Technology

When oil started gushing into the Gulf of Mexico in late April 2010, friends asked George Haller whether he was tracking its movement. That’s because the McGill engineering professor has been working for years on ways to better understand patterns in the seemingly chaotic motion of oceans and air. Meanwhile, colleagues of Josefina Olascoaga in Miami were asking the geophysicist a similar question. Fortunately, she was.

For those involved in managing the fallout from environmental disasters like the Deepwater Horizon oil spill, it is essential to have tools that predict how the oil will move, so that they make the best possible use of resources to control the spill. Thanks to work done by Haller and Olascoaga, such tools now appear to be within reach. Olascoaga’s computational techniques and Haller’s theory for predicting the movement of oil in water are equally applicable to the spread of ash in the air, following a volcanic explosion.

“In complex systems such as oceans and the atmosphere, there are a lot of features that we can’t understand offhand,” Haller explains. “People used to attribute these to randomness or chaos. But it turns out, when you look at data sets, you can find hidden patterns in the way that the air and water move.” Over the past decade, the team has developed mathematical methods to describe these hidden structures that are now broadly called Lagrangian Coherent Structures (LCSs), after the French mathematician Joseph-Louis Lagrange.

“Everyone knows about the Gulf Stream, and about the winds that blow from the West to the East in Canada,” says Haller, “but within these larger movements of air or water, there are intriguing local patterns that guide individual particle motion.” Olascoaga adds, “Though invisible, if you can imagine standing in a lake or ocean with one foot in warm water and the other in the colder water right beside it, then you have experienced an LCS running somewhere between your feet.”

“Ocean flow is like a busy city with a network of roads,” Haller says, “except that roads in the ocean are invisible, in motion, and transient.” The method Haller and Olascoaga have developed allows them to detect the cores of LCSs. In the complex network of ocean flows, these are the equivalent of “traffic intersections” and they are crucial to understanding how the oil in a spill will move. These intersections unite incoming flow from opposite directions and eject the resulting mass of water. When such an LCS core emerges and builds momentum inside the spill, we know that oil is bound to seep out within the next four to six days. This means that the researchers are now able to forecast dramatic changes in pollution patterns that have previously been considered unpredictable.

So, although Haller wasn’t tracking the spread of oil during the Deepwater Horizon disaster, he and Olascoaga were able to join forces to develop a method that does not simply track: it actually forecasts major changes in the way that oil spills will move. The two researchers are confident that this new mathematical method will help those engaged in trying to control pollution make well-informed decisions about what to do.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to University of Miami