Last month, a team led by Gary McGuire from University College Dublin in Ireland made an announcement: they had proven you can’t have a solvable Sudoku puzzle with less than 17 numbers already filled in.
Unlike most mathematical announcements, this was quickly picked up by the popular scientific media. Within a few days, the new finding had been announced in Nature and other outlets.
So where did this problem come from and why is its resolution interesting.
As you probably know, the aim of a Sudoku puzzle is to complete a partially-filled nine-by-nine grid of numbers. There are some guidelines: the numbers one to nine must appear exactly once each in every row, column and three-by-three sub-grid.
As with a crossword, a valid Sudoku puzzle must have a unique solution. There’s only one way to go from the initial configuration (with some numbers already filled in) to a completed grid.
Newspapers often grade their puzzles as easy, medium or hard, which will depend on how easy it is at every stage of solving the puzzle to fill in the “next” number. While a puzzle with a huge number of initial clues will usually be easy, it is not necessarily the case that a puzzle with few initial clues is difficult.
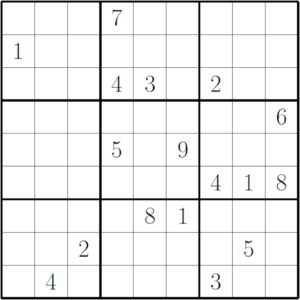
Reckon you can complete a 17-clue Sudoku puzzle? (answer below) Gordon Royle
When Sudoku-mania swept the globe in the mid-2000s, many mathematicians, programmers and computer scientists – amateur and professional – started to investigate Sudoku itself. They were less interested in solving individual puzzles, and more focused on asking and answering mathematical and/or computational questions about the entire universe of Sudoku puzzles and solutions.
As a mathematician specialising in the area of combinatorics (which can very loosely be defined as the mathematics of counting configurations and patterns), I was drawn to combinatorial questions about Sudoku.
I was particularly interested in the question of the smallest number of clues possible in a valid puzzle (that is, a puzzle with a unique solution).
In early 2005, I found a handful of 17-clue puzzles on a long-since forgotten Japanese-language website. By slightly altering these initial puzzles, I found a few more, then more, and gradually built up a “library” of 17-clue Sudoku puzzles which I made available online at the time.
Other people started to send me their 17-clue puzzles and I added any new ones to the list until, after a few years, I had collected more than 49,000 different 17-clue Sudoku puzzles.
By this time, new ones were few and far between, and I was convinced we had found almost all of the 17-clue puzzles. I was also convinced there was no 16-clue puzzle. I thought that demonstrating this would either require some new theoretical insight or clever programming combined with massive computational power, or both.
Either way, I thought proving the non-existence of a 16-clue puzzle was likely to be too difficult a challenge.
They key to McGuire’s approach was to tackle the problem indirectly. The total number of completed puzzles (that is, completely filled-in grids) is astronomical – 5,472,730,538 – and trying to test each of these to see if any choice of 16 cells from the completed grid forms a valid puzzle is far too time-consuming.
Instead, McGuire and colleagues used a different, indirect approach.
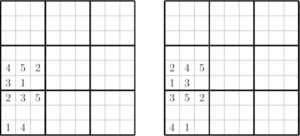
An “unavoidable set” in a completed Sudoku grid is a subset of the clues whose entries can be rearranged to leave another valid completed Sudoku grid. For a puzzle to be uniquely completable, it must contain at least one entry from every unavoidable set.
See the picture below to see what I mean.
If a completed grid contains the ten-clue configuration in the left picture, then any valid Sudoku puzzle must contain at least one of those ten clues. If it did not, then in any completed puzzle, those ten positions could either contain the left-hand configuration or the right-hand configuration and so the solution would not be unique.
Gordon Royle
While finding all the unavoidable sets in a given grid is difficult, it’s only necessary to find enough unavoidable sets to show that no 16 clues can “hit” them all. In the process of resolving this question, McGuire’s team developed new techniques for solving the “hitting set” problem.
It’s a problem that has many other applications – any situation in which a small set of resources must be allocated while still ensuring that all needs are met by at least one of the selected resources (i.e. “hit”) can be modelled as a hitting set problem.
Once the theory and software was in place, it was then a matter of running the programs for each of the 5.5 billion completed grids. As you can imagine, this required substantial computing power.
After 7 million core-CPU hours on a supercomputer (the equivalent of a single computer running for 7 million hours) and a year of actual elapsed time, the result was announced a few weeks ago, on New Year’s Day.
So is it correct?
The results of any huge computation should be evaluated with some caution, if not outright suspicion, especially when the answer is simply “no, doesn’t exist”, because there are many possible sources of error.
But in this case, I feel the result is far more likely to be correct than otherwise, and I expect it to be independently-verified before too long. In addition, McGuire’s team built on many different ideas, discussions and computer programs that were thrashed out between interested contributors to various online forums devoted to the mathematics of Sudoku. In this respect, many of the basic components of their work have already been thoroughly tested.
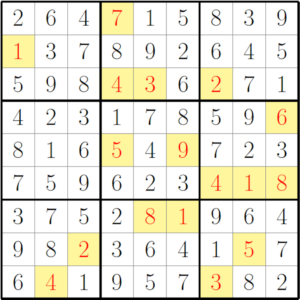
Solution to the 17-clue Sudoku puzzle, above. Gordon Royle
And so back to the question: why is the resolution of this problem interesting? And is it important?
Certainly, knowing that the smallest Sudoku puzzles have 17 clues is not in itself important. But the immense popularity of Sudoku meant that this question was popularised in a way that many similar questions have never been, and so it took on a special role as a “challenge question” testing the limits of human knowledge.
The school students to whom I often give outreach talks have no real concept of the limitations of computers and mathematics. In my past talks, these students were almost always astonished to know that the answer to such a simple question was just not known.
And now, in my future outreach talks, I will describe how online collaboration, theoretical development and significant computational power were combined to solve this problem, and how this process promises to play an increasing role in the future development of mathematics.
For more such insights, log into our website https://international-maths-challenge.com
Credit of the article given to Gordon Royle, The University of Western Australia





