Month: May 2018

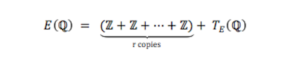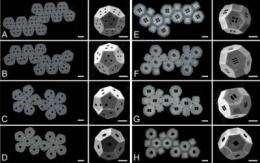
This showas a few of the 2.3 million possible 2-D designs — planar nets — for a truncated octahedron (right column). The question is: Which net is best to make a self-assembling shape at the nanoscale?

Material chemists and engineers would love to figure out how to create self-assembling shells, containers or structures that could be used as tiny drug-carrying containers or to build 3-D sensors and electronic devices.

There have been some successes with simple 3-D shapes such as cubes, but the list of possible starting points that could yield the ideal self-assembly for more complex geometric configurations gets long fast. For example, while there are 11 2-D arrangements for a cube, there are 43,380 for a dodecahedron (12 equal pentagonal faces). Creating a truncated octahedron (14 total faces – six squares and eight hexagons) has 2.3 million possibilities.

“The issue is that one runs into a combinatorial explosion,” said Govind Menon, associate professor of applied mathematics at Brown University. “How do we search efficiently for the best solution within such a large dataset? This is where math can contribute to the problem.”

In a paper published in the Proceedings of National Academy of Sciences, researchers from Brown and Johns Hopkins University determined the best 2-D arrangements, called planar nets, to create self-folding polyhedra with dimensions of a few hundred microns, the size of a small dust particle. The strength of the analysis lies in the combination of theory and experiment. The team at Brown devised algorithms to cut through the myriad possibilities and identify the best planar nets to yield the self-folding 3-D structures. Researchers at Johns Hopkins then confirmed the nets’ design principles with experiments.

“Using a combination of theory and experiments, we uncovered design principles for optimum nets which self-assemble with high yields,” said David Gracias, associate professor in of chemical and biomolecular engineering at Johns Hopkins and a co-corresponding author on the paper. “In doing so, we uncovered striking geometric analogies between natural assembly of proteins and viruses and these polyhedra, which could provide insight into naturally occurring self-assembling processes and is a step toward the development of self-assembly as a viable manufacturing paradigm.”

“This is about creating basic tools in nanotechnology,” said Menon, co-corresponding author on the paper. “It’s important to explore what shapes you can build. The bigger your toolbox, the better off you are.”

While the approach has been used elsewhere to create smaller particles at the nanoscale, the researchers at Brown and Johns Hopkins used larger sizes to better understand the principles that govern self-folding polyhedra.

The researchers sought to figure out how to self-assemble structures that resemble the protein shells viruses use to protect their genetic material. As it turns out, the shells used by many viruses are shaped like dodecahedra (a simplified version of a geodesic dome like the Epcot Center at Disney World). But even a dodecahedron can be cut into 43,380 planar nets. The trick is to find the nets that yield the best self-assembly. Menon, with the help of Brown undergraduate students Margaret Ewing and Andrew “Drew” Kunas, sought to winnow the possibilities. The group built models and developed a computer code to seek out the optimal nets, finding just six that seemed to fit the algorithmic bill.

The students got acquainted with their assignment by playing with a set of children’s toys in various geometric shapes. They progressed quickly into more serious analysis. “We started randomly generating nets, trying to get all of them. It was like going fishing in a lake and trying to count all the species of fish,” said Kunas, whose concentration is in applied mathematics. After tabulating the nets and establishing metrics for the most successful folding maneuvers, “we got lists of nets with the best radius of gyration and vertex connections, discovering which nets would be the best for production for the icosahedron, dodecahedron, and truncated octahedron for the first time.”

Gracias and colleagues at Johns Hopkins, who have been working with self-assembling structures for years, tested the configurations from the Brown researchers. The nets are nickel plates with hinges that have been soldered together in various 2-D arrangements. Using the options presented by the Brown researchers, the Johns Hopkins’s group heated the nets to around 360 degrees Fahrenheit, the point at which surface tension between the solder and the nickel plate causes the hinges to fold upward, rotate and eventually form a polyhedron. “Quite remarkably, just on heating, these planar nets fold up and seal themselves into these complex 3-D geometries with specific fold angles,” Gracias said.

“What’s amazing is we have no control over the sequence of folds, but it still works,” Menon added.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Karolina Grabowska/Pexels,

Elliptic curves have a long and distinguished history that can be traced back to antiquity. They are prevalent in many branches of modern mathematics, foremost of which is number theory.

In simplest terms, one can describe these curves by using a cubic equation of the form

where A and B are fixed rational numbers (to ensure the curve E is nice and smooth everywhere, one also needs to assume that its discriminant 4A³ + 27B² is non-zero).

To illustrate, let’s consider an example: choosing A=-1 and B=0, we obtain the following picture:

At this point it becomes clear that, despite their name, elliptic curves have nothing whatsoever to do with ellipses! The reason for this historical confusion is that these curves have a strong connection to elliptic integrals, which arise when describing the motion of planetary bodies in space.

The ancient Greek mathematician Diophantus is considered by many to be the father of algebra. His major mathematical work was written up in the tome Arithmetica which was essentially a school textbook for geniuses. Within it, he outlined many tools for studying solutions to polynomial equations with several variables, termed Diophantine Equations in his honour.

One of the main problems Diophantus considered was to find all solutions to a particular polynomial equation that lie in the field of rational numbers Q. For equations of “degree two” (circles, ellipses, parabolas, hyperbolas) we now have a complete answer to this problem. This answer is thanks to the late German mathematician Helmut Hasse, and allows one to find all such points, should they exist at all.

Returning to our elliptic curve E, the analogous problem is to find all the rational solutions (x,y) which satisfy the equation defining E. If we call this set of points E(Q), then we are asking if there exists an algorithm that allows us to obtain all points (x,y) belonging to E(Q).

At this juncture we need to introduce a group law on E, which gives an eccentric way of fusing together two points (p₁ and p₂) on the curve, to obtain a brand new point (p₄). This mimics the addition law for numbers we learn from childhood (i.e. the sum or difference of any two numbers is still a number). There’s an illustration of this rule below:

Under this geometric model, the point p₄ is defined to be the sum of p₁ and p₂ (it’s easy to see that the addition law does not depend on the order of the points p₁, p₂). Moreover the set of rational points is preserved by this notion of addition; in other words, the sum of two rational points is again a rational point.

Louis Mordell, who was Sadleirian Professor of Pure Mathematics at Cambridge University from 1945 to 1953, was the first to determine the structure of this group of rational points. In 1922 he proved

where the number of copies of the integers Z above is called the “rank r(E) of the elliptic curve E”. The finite group Τ_E(Q) on the end is uninteresting, as it never has more than 16 elements.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Daniel Delbourgo*

The problem’s been solved … but the sweet treats were declined. Back to the Cutting Board

In 1904, French mathematician Henri Poincaré asked a key question about three-dimensional spaces (“manifolds”).

Imagine a piece of rope, so that firstly a knot is tied in the rope and then the ends are glued together. This is what mathematicians call a knot. A link is a collection of knots that are tangled together.

It has been observed that DNA, which is coiled up within cells, occurs in closed knotted form.

Complex molecules such as polymers are tangled in knotted forms. There are deep connections between knot theory and ideas in mathematical physics. The outsides of a knot or link in space give important examples of three-dimensional spaces.

Torus. Fropuff

Back to Poincaré and his conjecture. He asked if the 3-sphere (which can be formed by either adding a point at infinity to ordinary three-dimensional Euclidean space or by gluing two solid three-dimensional balls together along their boundary 2-spheres) was the only three-dimensional space in which every loop can be continuously shrunk to a point.

Poincaré had introduced important ideas in the structure and classification of surfaces and their higher dimensional analogues (“manifolds”), arising from his work on dynamical systems.

Donuts to go, please

A good way to visualise Poincaré’s conjecture is to examine the boundary of a ball (a two-dimensional sphere) and the boundary of a donut (called a torus). Any loop of string on a 2-sphere can be shrunk to a point while keeping it on the sphere, whereas if a loop goes around the hole in the donut, it cannot be shrunk without leaving the surface of the donut.

Many attempts were made on the Poincaré conjecture, until in 2003 a wonderful solution was announced by a young Russian mathematician, Grigori “Grisha” Perelman.

This is a brief account of the ideas used by Perelman, which built on work of two other outstanding mathematicians, Bill Thurston and Richard Hamilton.

3D spaces

Thurston made enormous strides in our understanding of three-dimensional spaces in the late 1970s. In particular, he realised that essentially all the work that had been done since Poincaré fitted into a single theme.

He observed that known three-dimensional spaces could be divided into pieces in a natural way, so that each piece had a uniform geometry, similar to the flat plane and the round sphere. (To see this geometry on a torus, one must embed it into four-dimensional space!).

Thurston made a bold “geometrisation conjecture” that this should be true for all three-dimensional spaces. He had many brilliant students who further developed his theories, not least by producing powerful computer programs that could test any given space to try to find its geometric structure.

Thurston made spectacular progress on the geometrisation conjecture, which includes the Poincaré conjecture as a special case. The geometrisation conjecture predicts that any three-dimensional space in which every loop shrinks to a point should have a round metric – it would be a 3-sphere and Poincaré’s conjecture would follow.

In 1982, Richard Hamilton published a beautiful paper introducing a new technique in geometric analysis which he called Ricci flow. Hamilton had been looking for analogues of a flow of functions, so that the energy of the function decreases until it reaches a minimum. This type of flow is closely related to the way heat spreads in a material.

Hamilton reasoned that there should be a similar flow for the geometric shape of a space, rather than a function between spaces. He used the Ricci tensor, a key feature of Einstein’s field equations for general relativity, as the driving force for his flow.

He showed that, for three-dimensional spaces where the Ricci curvature is positive, the flow gradually changes the shape until the metric satisfies Thurston’s geometrisation conjecture.

Hamilton attracted many outstanding young mathematicians to work in this area. Ricci flow and other similar flows have become a huge area of research with applications in areas such as moving interfaces, fluid mechanics and computer graphics.

Ricci flow. CBN

He outlined a marvellous program to use Ricci flow to attack Thurston’s geometrisation conjecture. The idea was to keep evolving the shape of a space under Ricci flow.

Hamilton and his collaborators found the space might form a singularity, where a narrow neck became thinner and thinner until the space splits into two smaller spaces.

Hamilton worked hard to try to fully understand this phenomenon and to allow the pieces to keep evolving under Ricci flow until the geometric structure predicted by Thurston could be found.

Perelman

This is when Perelman burst on to the scene. He had produced some brilliant results at a very young age and was a researcher at the famous Steklov Institute in St Petersburg. Perelman got a Miller fellowship to visit UC Berkeley for three years in the early 1990s.

I met him there around 1992. He then “disappeared” from the mathematical scene for nearly ten years and re-emerged to announce that he had completed Hamilton’s Ricci flow program, in a series of papers he posted on the electronic repository called ArXiv.

His papers created enormous excitement and within several months a number of groups had started to work through Perelman’s strategy.

Eventually everyone was convinced that Perelman had indeed succeeded and both the geometrisation and Poincaré conjecture had been solved.

Perelman was awarded both a Fields medal (the mathematical equivalent of a Nobel prize) and also offered a million dollars for solving one of the Millenium prizes from the Clay Institute.

He turned down both these awards, preferring to live a quiet life in St Petersburg. Mathematicians are still finding new ways to use the solution to the geometrisation conjecture, which is one of the outstanding mathematical results of this era.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Hyam Rubinstein*

When the statistician for UC Irvine’s innovative Down syndrome program retired last year, its researchers were left in a bind. The group is studying ways to prevent or delay the onset of Alzheimer’s-type dementia in people with Down syndrome, including examining possible links between seizures and cognitive decline.

“We were mid-study when we found ourselves with no statistician and little budget with which to pay one,” explains program manager Eric Doran.

Statistical analysis for the project was critical and especially difficult. Some of the subjects’ dementia had progressed to the point that they could no longer be tested on performance-based cognitive measures. They couldn’t respond to questions, making it hard for clinicians to evaluate them. But that resulted in missing data. How, then, could the team accurately quantify change over time and see whether seizures might play a role?

Enter Vinh Nguyen, then a doctoral student in statistics at the Donald Bren School of Information & Computer Sciences and now the new head of the UCI Center for Statistical Consulting, which aims to help researchers across campus and Orange County with such challenges. He proposed a model to gauge how quickly people were becoming untestable, instead of how fast they declined. Rather than including test scores – which would have been zero for those who couldn’t be quizzed – Nguyen designed a variable to show when they became unable to respond.

“My part of it was to help them find a way to look at patients with and without seizures, to see if those with seizures might have a shorter time before they became untestable,” he says. “That’s what we found.”Although the findings are preliminary, without his involvement they wouldn’t have been possible. The work resulted in a paper that has been accepted for publication in the Journal of Alzheimer’s Disease. Nguyen, as of October an assistant professor-in-residence of statistics, is a co-author.

“We’re very fortunate to have Vinh’s assistance,” Doran says. “Quite frankly, some of the statistical analysis he’s doing goes well beyond the skill level of even the most seasoned investigators. Vinh was able to pick up where our previous statistician left off, and he was pretty ingenious. His creative look at the data enabled us to complete our analysis.”

Nguyen was glad to help: “I’m excited to be involved in studies that not only advance science but also make a meaningful impact in people’s lives.”

He looks forward to doing more such work through the center, providing state-of-the-art statistical expertise in grant preparation, the design of studies and experiments, and data analysis. The center this spring will offer free statistical consulting for campus researchers via a course taught by Dr. Nguyen. Graduate students in the class will be assigned to projects based on their interests and skills.

“It’s a huge benefit to the university because it’s free, and it’s a huge benefit to the statistics graduate program because it gives our master’s and Ph.D. students a chance to exercise their knowledge and training in real-world applications,” Nguyen says. “Learning how to communicate, how to collaborate with folks outside your field – you can’t just lecture about that. It’s got to be a hands-on experience.”

Colleagues say Nguyen, 26 – whose research interests include survival analysis, robust statistical methods, sequential clinical trials and prediction – was the right choice to run the center.

“It’s a big set of responsibilities for someone so young, but he’s got the ability and maturity level to succeed,” says associate professor of statistics Dan Gillen, who directs statistics research at the Institute for Memory Impairments & Neurological Disorders. It was Gillen who introduced Nguyen, whom he was advising on his doctoral thesis, to the Down syndrome team. “Vinh understands the role of statistics across multiple branches of science, and he’s extremely good at translating a seemingly vague hypothesis into a precise statistical framework.”

A native of Vietnam, Nguyen immigrated to the United States at age 5 and grew up in Garden Grove. A true-blue Anteater, he earned all his degrees at UCI, graduating magna cum laude with a B.S. in mathematics and a B.A. in economics, then obtaining an M.S. and a Ph.D. in statistics. In 2010, he received an Achievement Rewards for College Scientists scholar award, which recognizes UCI’s academically superior doctoral students who exhibit outstanding promise as scientists, researchers and public leaders.

“I feel very fortunate to be here,” Nguyen says. “I’m honoured to be given this opportunity to lead the center and help it grow, and to work in a field and a setting that allow me to apply my knowledge.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Rizza Barnes, University of California, Irvine