When you look at a train or university timetable you don’t think about how the timetable was made – you’re thinking about your trip or where your next class is.
In that moment, you couldn’t care less about all the juggling and compromising that needs to happen to get a timetable working.
Not surprisingly, though, this is a difficult process dating back many years and one that perplexes mathematicians even today.
To understand the difficulty associated with creating timetables – those timetables we all rely so heavily on – we need to understand the nature of difficulty itself.
In particular, we need to understand how it applies in a mathematical context.
Seriously, how hard can it be?
Not surprisingly, some tasks in mathematics are harder than others – but even this perception is complicated. Many important computational tasks are hard, or at least appear to be hard.
Knowing precisely what “hard” and “easy” mean has itself turned out to be extremely challenging. To really know a computational task is hard, we have to really know that there isn’t some nice efficient method waiting to be discovered that would render the task straightforward.
Our old friend timetabling is a classic example of a problem for which the precise difficulty is unknown.
I don’t get it, and my train’s leaving …
Consider a university timetable: a computer can easily check that such a timetable has no clashes but a clash-free timetable cannot (in general) be guaranteed. Because of this, finding a timetable with the minimum number of clashes is a genuine mathematical challenge.
Commercial timetabling applications can’t in general do any better than attempt to approximate the minimum number of clashes.
As yet, no-one has yet proved that timetabling cannot be solved efficiently. In fact, the ability to solve timetabling efficiently hinges on one of the foremost unsolved problems in mathematics: the so-called “P vs NP” problem.
A Millennium Problem
Roughly speaking, the “P vs NP” problem asks whether:
1) finding correct solutions to a problem (e.g. constructing a clash-free timetable) is genuinely harder task than …
2) … simply checking a given correct solution (e.g. checking to see if a completed timetable is clash-free).
Intuitively, you would believe finding a solution should be harder than checking a solution.
Think of your favourite Sudoku puzzle: checking that your solution is correct is easy – each square, column and row can only contain each number from one to nine once. But finding the solution – completing the puzzle – is hard graft.
But it’s not quite as simple as that.
In 2000, the Clay Institute chose “P vs NP” as one of seven Millennium Prize problems, with a $1 million prize for the person who solves it.
Constraint satisfaction
Algebraic and logical methods have proved particularly useful in understanding what determines the difficulty of a problem.
Among the computational problems in the NP class – i.e. problems that can’t “easily” be solved by a computer – Constraint Satisfaction Problems (or CSPs, as they are affectionately known) have received particular attention.
Any problem that involves giving values to a large collection of objects that obey some constraints is a CSP – and timetabling is one such problem.
In a school or university setting, we assign exam slots to particular subjects, obeying the constraint that subjects with common enrollment are scheduled at different times.
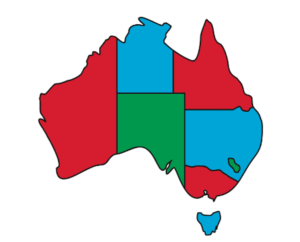
Map colouring is a CSP closely related to timetabling. In the above image we gave each state and territory one of three colours – red, green or blue – with the constraint that neighbouring states and territories must have different colours.
Map colouring is typical of “hard” problems in the class NP: given a successfully three-coloured map it is easy to verify that it obeys the neighbouring region constraint (so checking is easy). But in general there is no known efficient algorithm for deciding if a map can be a successfully three-coloured.
With every CSP one may associate an algebraic structure, but be warned: even by the imaginative standards of modern algebra, these structures are unusual beasts.
Numbers of the beast
In the familiar high school “algebra of numbers”, operations such as addition and multiplication are used to combine numbers to produce new ones. So, combining 1 and 2 using + gives 3.
For a CSP such as timetabling though, the role of numbers is taken by the available timetable slots, and the operations used to combine these are even more bizarre.
(How bizarre are these operations? Well, they are “technical generalisations of symmetries”, known as “polymorphisms”. You did ask!)
Despite their unusual character, these weird algebraic oddities are known to precisely determine the difficulty of a CSP.
A problem such as timetabling turns out to have very few polymorphisms: a classic hallmark of a difficult problem.
Many mathematicians and theoretical computer scientists around the world are working hard to prove it is precisely this absence of interesting properties that causes computational difficulty.
Will anyone ever solve this mighty head-scratcher? The chance of winning a Millenium Prize – not to mention $1 million – is definitely a motivating factor.
For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to Peter Rowlett*




