Cracking this mathematical mystery will make someone rich, but its value to all of us could be incalculable. Jacob Aron explains why it matters if P = NP.
Dear Fellow Researchers, I am pleased to announce a proof that P is not equal to NP, which is attached in 10pt and 12pt fonts.” So began an email sent in August 2010 to a group of leading computer scientists by Vinay Deolalikar, a mathematician at Hewlett-Packard Labs in Palo Alto, California.
It was an incendiary claim. Deolalikar was saying he had cracked the biggest problem in computer science, a question concerning the complexity and fundamental limits of computation. Answer the question “Is P equal to NP?” with a yes, and you could be looking at a world transformed, where planes and trains run on time, accurate electronic translations are routine, the molecular mysteries of life are revealed at the click of a mouse – and secure online shopping becomes fundamentally impossible. Answer it with a no, as Deolalikar claimed to have done, and it would suggest that some problems are too irreducibly complex for computers to solve exactly.
One way or another, then, we would like an answer. But it has been frustratingly slow in coming. “It’s turned out to be an incredibly hard problem,” says Stephen Cook of the University of Toronto, Canada, the computer scientist who first formulated it in May 1971. “I never thought it was going to be easy, but now 40 years later it looks as difficult as ever.”
The importance of P = NP? was emphasised in 2000, when the privately funded Clay Mathematics Institute in Cambridge, Massachusetts, named it as one of seven “Millennium Prize” problems, with a $1 million bounty for whoever solves it. Since then Cook and other researchers in the area have regularly received emails with purported solutions. Gerhard Woeginger of the Eindhoven University of Technology in the Netherlands even maintains an online list of them. “We’ve seen hundreds of attempts, and we can more or less classify them according to the mistakes the proof makes,” he says.
Deolalikar’s attempt seemed different. For a start, it came from an established researcher rather than one of the legion of amateurs hoping for a pop at glory and a million dollars. Also, Cook initially gave it a cautious thumbs up, writing that it seemed to be a “relatively serious claim”. That led it to spread across the web and garnered it widespread attention in the press, New Scientist included (14 August 2010, p 7).
In the end, though, it was a false dawn. “It probably didn’t deserve all the publicity,” says Neil Immerman, a computer scientist at the University of Massachusetts, Amherst. He was one of an army of researchers who, working in an informal online collaboration, soon exposed fundamental flaws in the proof. Deolalikar has responded to some of them and submitted an expanded version to an academic journal. Till he hears back, he refuses to comment further.
The consensus now is that his proof – like all attempts before it – is unfixable. And so the mystique of P = NP? remains unbroken 40 years on. But what is the problem about? Why is it so important, and what happens if it is answered one way or the other?
“The consensus now is that last year’s proof is false – which just adds to the mystique of the problem”
What is P?
Computing power, we are accustomed to think, is the gift that keeps on giving. Every year or two that goes by sees roughly a doubling in our number-crunching capabilities – a march so relentless that it has acquired the label “Moore’s law”, after the Intel researcher, Gordon Moore, who first noted the trend back in the 1960s.
Talk of the ultimate limits of computation tends to be about how many transistors, the building blocks of microprocessors, we can cram onto a conventional silicon chip – or whatever technology or material might replace it. P = NP? raises the spectre that there is a more fundamental limitation, one that lies not in hardware but in the mechanics of computation itself.
P = NP should not be mistaken for a simple algebraic equation – if it were, we could just have N = 1 and claim the Clay institute’s million bucks. P and NP are examples of “complexity classes”, categories into which problems can be slotted depending on how hard it is to unravel them using a computer.
Solving any problem computationally depends on finding an algorithm, the step-by-step set of mathematical instructions that leads us to the answer. But how much number-crunching does an algorithm need? That depends on the problem.
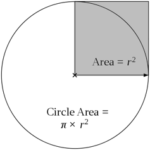
The P class of problems is essentially the easy ones: an algorithm exists to solve them in a “reasonable” amount of time. Imagine looking to see if a particular number appears in a list. The simplest solution is a “linear search” algorithm: you check each number in turn until you find the right one. If the list has n numbers – the “size” of the problem – this algorithm takes at most n steps to search it, so its complexity is proportional to n. That counts as reasonable. So too do things that take a little more computational muscle – for instance, the manual multiplication of two n-digit numbers, which takes about n2 steps. A pocket calculator will still master that with ease, at least for relatively small values of n. Any problem of size n whose solution requires n to the power of something (nx) steps is relatively quick to crack. It is said to be solvable in “polynomial time”, and is denoted P.
What is NP?
Not all problems are as benign. In some cases, as the size of the problem grows, computing time increases not polynomially, as nx, but exponentially, as xn – a much steeper increase. Imagine, for example, an algorithm to list out all possible ways to arrange the numbers from 1 to n. It is not difficult to envisage what the solutions are, but even so the time required to list them rapidly runs away from us as n increases. Even proving a problem belongs to this non-polynomial class can be difficult, because you have to show that absolutely no polynomial-time algorithm exists to solve it.
That does not mean we have to give up on hard problems. With some problems that are difficult to solve in a reasonable time, inspired guesswork might still lead you to an answer whose correctness is easy to verify. Think of a sudoku puzzle. Working out a solution can be fiendishly difficult, even for a computer, but presented with a completed puzzle, it is easy to check that it fulfils the criteria for being a valid answer (see diagram). Problems whose solutions are hard to come by but can be verified in polynomial time make up the complexity class called NP, which stands for non-deterministic polynomial time.
Constructing a valid sudoku grid – in essence asking the question “Can this number fill this space?” over and over again for each space and each number from 1 to 9, until all spaces are compatibly filled – is an example of a classic NP problem, the Boolean satisfiability problem. Processes such as using formal logic to check software for errors and deciphering the action of gene regulatory networks boil down to similar basic satisfiability problems.
And here is the nub of the P = NP? problem. All problems in the set P are also in the set NP: if you can easily find a solution, you can easily verify it. But is the reverse true? If you can easily verify the solution to a problem, can you also easily solve it – is every problem in the set NP also in P? If the answer to that question is yes, the two sets are identical: P is equal to NP, and the world of computation is irrevocably changed – sudoku becomes a breeze for a machine to solve, for starters. But before we consider that possibility, what happens if P is found to be not equal to NP?
What if P ≠ NP?
In 2002, William Gasarch, a computer scientist at the University of Maryland in College Park, asked 100 of his peers what they thought the answer to the P = NP? question would be. “You hear people say offhand what they think of P versus NP. I wanted to get it down on record,” he says. P ≠ NP was the overwhelming winner, with 61 votes. Only nine people supported P = NP, some, they said, just to be contrary. The rest either had no opinion or deemed the problem impossible to solve.
If the majority turns out to be correct, and P is not equal to NP – as Deolalikar suggested – it indicates that some problems are by their nature so involved that we will never be able to crunch through them. If so, the proof is unlikely to make a noticeable difference to you or me. In the absence of a definitive answer to P = NP?, most computer scientists already assume that some hard problems cannot be solved exactly. They concentrate on designing algorithms to find approximate solutions that will suffice for most practical purposes. “We’ll be doing exactly the same as we’re currently doing,” says Woeginger.
Proving P ≠ NP would still have practical consequences. For a start, says Immerman, it would shed light on the performance of the latest computing hardware, which splits computations across multiple processors operating in parallel. With twice as many processors, things should run twice as fast – but for certain types of problem they do not. That implies some kind of limitation to computation, the origin of which is unclear. “Some things seem like they’re inherently sequential,” says Immerman. “Once we know that P and NP are not equal, we’ll know why.”
It could also have an impact on the world of cryptography. Most modern encryption relies on the assumption that breaking a number down to its prime-number factors is hard. This certainly looks like a classic NP problem: finding the prime factors of 304,679 is hard, but it’s easy enough to verify that they are 547 and 557 by multiplying them together. Real encryption uses numbers with hundreds of digits, but a polynomial-time algorithm for solving NP problems would crack even the toughest codes.
So would P ≠ NP mean cryptography is secure? Not quite. In 1995, Russell Impagliazzo of the University of California, San Diego, sketched out five possible outcomes of the P = NP? debate. Four of them were shades-of-grey variations on a world where P ≠ NP. For example, we might find some problems where even though the increase in complexity as the problem grew is technically exponential, there are still relatively efficient ways of finding solutions. If the prime-number-factoring problem belongs to this group, cryptography’s security could be vulnerable, depending where reality lies on Impagliazzo’s scale. “Proving P is not equal to NP isn’t the end of our field, it’s the beginning,” says Impagliazzo.
Ultimately, though, it is the fifth of Impagliazzo’s worlds that excites researchers the most, however unlikely they deem it. It is “Algorithmica” – the computing nirvana where P is indeed equal to NP.
What if P = NP?
If P = NP, the revolution is upon us. “It would be a crazy world,” says Immerman. “It would totally change our lives,” says Woeginger.
That is because of the existence, proved by Cook in his seminal 1971 paper, of a subset of NP problems known as NP-complete. They are the executive key to the NP washroom: find an algorithm to solve an NP-complete problem, and it can be used to solve any NP problem in polynomial time.
Lots of real-world problems are known to be NP-complete. Satisfiability problems are one example; versions of the knapsack problem (below), which deals with optimal resource allocation, and the notorious travelling salesman problem (above) are others. This problem aims to find the shortest-distance route for visiting a series of points and returning to the starting point, an issue of critical interest in logistics and elsewhere.
If we could find a polynomial-time algorithm for any NP-complete problem, it would prove that P=NP, since all NP problems would then be easily solvable. The existence of such a universal computable solution would allow the perfect scheduling of transport, the most efficient distribution of goods, and manufacturing with minimal waste – a leap and a bound beyond the “seems-to-work” solutions we now employ.
It could also lead to algorithms that perform near-perfect speech recognition and language translation, and that let computers process visual information as well as any human can. “Basically, you would be able to compute anything you wanted,” says Lance Fortnow, a computer scientist at Northwestern University in Evanston, Illinois. A further curious side effect would be that of rendering mathematicians redundant. “Mathematics would be largely mechanisable,” says Cook. Because finding a mathematical proof is difficult, but verifying one is relatively easy, in some way maths itself is an NP problem. If P=NP, we could leave computers to churn out new proofs.
“Proving P = NP would have the curious side effect of rendering mathematicians redundant”
What if there’s no algorithm?
There is an odd wrinkle in visions of a P = NP world: that we might prove the statement to be true, but never be able to take advantage of that proof. Mathematicians sometimes find “non-constructive proofs” in which they show that a mathematical object exists without actually finding it. So what if they could show that an unknown P algorithm exists to solve a problem thought to be NP? “That would technically settle the problem, but not really,” says Cook.
There would be a similar agonising limbo if a proof that P=NP is achieved with a universal algorithm that scales in complexity as n to the power of a very large number. Being polynomial, this would qualify for the Clay institute’s $1 million prize, but in terms of computability it would not amount to a hill of beans.
Will we have an answer soon?
When can we expect the suspense to be over, one way or another? Probably not so soon. “Scientometrist” Samuel Arbesman of the Harvard Medical School in Boston, Massachusetts, predicts that a solution of “P = NP?” is not likely to arrive before 2024 (New Scientist, 25 December 2010, p 24). In Gasarch’s 2002 poll of his peers, only 45 per cent believed it would be resolved by 2050. “I think people are now more pessimistic,” he says, “because after 10 years there hasn’t been that much progress.” He adds that he believes a proof could be up to 500 years away.
Others find that excessively gloomy, but all agree there is a mammoth task ahead. “The current methods we have don’t seem to be giving us progress,” says Fortnow. “All the simple ideas don’t work, and we don’t know where to look for new tools,” says Woeginger. Part of the problem is that the risk of failure is too great. “If you have already built up a reputation, you don’t want to publish something that makes other people laugh,” says Woeginger.
Some are undeterred. One is Ketan Mulmuley at the University of Chicago. He declined to comment on his work, which is currently under review for publication, but fellow researchers say his ideas look promising. In essence it involves translating the P = NP? problem into more tractable problems in algebraic geometry, the branch of mathematics that relates shapes and equations. But it seems even Mulmuley is not necessarily anticipating a quick success. “He expects it to take well over 100 years,” says Fortnow.
Ultimately, though, Mulmuley’s tactic of connecting P = NP? to another, not obviously related, mathematical area seems the most promising line of attack. It has been used before: in 1995, the mathematician Andrew Wiles used work linking algebraic geometry and number theory to solve another high-profile problem, Fermat’s last theorem. “There were a lot of building blocks,” says Fortnow. “Then it took one brilliant mind to make that last big leap.”
Woeginger agrees: “It will be solved by a mathematician who applies methods from a totally unrelated area, that uses something nobody thinks is connected to the P versus NP question.” Perhaps the person who will settle P = NP? is already working away in their own specialised field, just waiting for the moment that connects the dots and solves the world’s hardest problem.
For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to Jacob Aron*