Month: May 2017

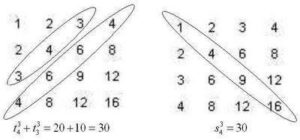
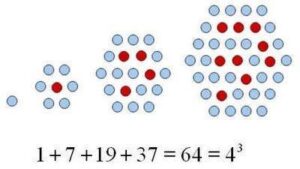
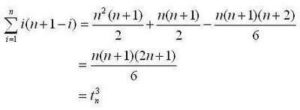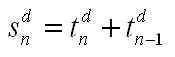There is a nice identity stating that a square number can be written as the sum of two subsequent triangular numbers.

Here we are writing tdn for the nth triangular of dimension d (d=2 are the flat polygonals, d=3 for they pyramidal polygonals, etc.)

There is also a nice relationship that connects cubes to polygonal numbers. It turns out that a cube of spheres can be unfolded into a packed-hexagonal pyramid. The “packed hexagonals” or “centered hexagonals” are not quite the usual hexagonal numbers – instead these are hexagons of dots with the gaps filled in. The picuture below shows how square numbers fill the gaps of the hexagonals perfectly to form the “packed hexagonals,” and how these in turn can be stacked to form a cube. Here we are using phdn for “packed hexagonals” hdn for hexagonals, sdn for squares, and tdn for triangular numbers.

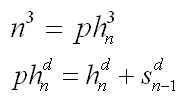
Combining this result with the “triangulation” identities we have:

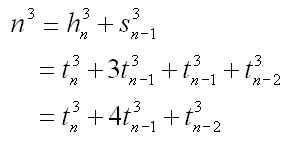
This gives us three nice identities for powers of n:

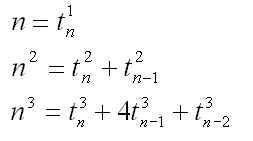
It turns out that these identities generalize for other positive integer powers of n. Every nd can be written as a sum of tdi where i ranges from n to n+1−d. (for any i less than 1, these terms are zero)

1.Write out the sequence of nd for at least 2d−2 terms. Take the finite difference of this sequence d−2 times (this reduces the sequence down to “2-dimensional” numbers, allowing us to use the 2-dimensional triangular numbers in our calculations).

2.The first term of the new sequence should be 1. Eliminate the first term by subtracting t2n from this sequence. This means that our sum begins with tdn, with a coefficient of 1. Ensure that the t2n values are subtracted from the corresponding terms of the sequence.

3. Now, the sequence has a new first term which is A. Eliminate this term by subtracting A t2n from the sequence. A is the coefficient of tdn−1.

4. Repeat step 3, eliminating the first term of the sequence each time with a multiple of t2n, which provides the coefficient for the next value of tdi.

5.The process ends when all terms in the nd sequence is eliminated, which happens at the dth step.

Carrying out this process for a few more powers of n, we end up with:

In general, we seem to have:

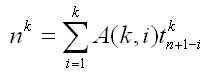
where the coefficients A(i,k) have the nice properties:

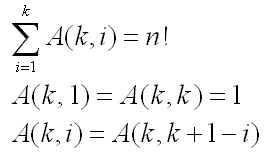
The coefficients are naturally analogous to the binomial coefficients, and can be arranged in a triangle like Pascal’s.

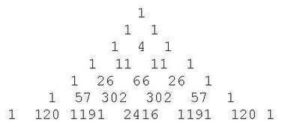
These coefficients are known as Eulerian numbers, and the construction above is known as Euler’s Number Triangle (not to be confused with the geometric construction called the Euler Triangle).

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to dan.mackinnon*

If mathematics is a game, then playing some game is doing mathematics, and in that case why isn’t dancing mathematics too?

Ludwig Wittgenstein – Remarks on the Foundations of Mathematics

Mathematics is often described metaphorically – the  forms that these metaphors take include the organic, mechanical, classical, and post-modern, among countless others. Within these metaphors, mathematics may be a tool, or set of tools, a tree, part of a tree, a vine, a game, or set of games, and mathematicians in turn may be machines, game-players, artists, inventors, or explorers.

Despite the many metaphors used to describe mathematics, in popular discourse mathematics is often reduced to one of its parts, being metonymically described as merely about numbers, formulas, or some other limited aspect. Metaphor is a more complete substitution of ideas than metonymy – allowing us to link concepts that do not appear to have any direct relationship. Perhaps, metaphoric language that elevates and expands our ideas about mathematics is used by enthusiasts to counter the more limited and diminishing metonymic descriptions that are often encountered.

Attempts to describe and elevate mathematics through metaphor seem to fall short, however. Our usual way of thinking about things is to inquire about their meaning – a meaning that is assumed to lie beneath or beyond mere appearances. Metaphor generally relies on making connections between concepts on this deeper level. The sheer formalism of mathematics frustrates this usual way of thinking, and leaves us grasping for a meaning that is constantly evasive. The sheer number and variety of the  many metaphors for mathematics suggests that no single convincing one has yet been found. It may be that the repeated attempts to find such a unifying metaphor represents an ongoing and forever failing attempt to grapple with the purely formal character of mathematics; and it may be that the formal nature of mathematics will always shake off any metaphor that attempts to tie it down.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to dan.mackinnon*

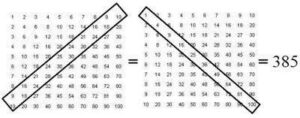A surprising relationship found in the multiplication table is that the sum of the entries in the main upwards diagonal and the diagonal above it is equal to the sum of the entries in the main downwards diagonal. What is also surprising is that this is but one among several observations about the multiplication table that can be expressed in terms of polygonal numbers.

This relationship involves three-dimensional triangular numbers (triangle-based pyramidal numbers, or tetrahedral numbers), and three-dimensional square numbers (square-based pyramidal numbers). Some values for these, and a few other polygonals, are shown below.

To see why this relationship holds, first note that the sum of the entries in the nth upward diagonal in the multiplication table is equal to the nth three-dimensional triangular number.

Second, observe that he entries in the main down diagonal are square numbers (two-dimensional), so the sum of the main down diagonal is the nth three-dimensional square number.

Finally, we use the fact that a square number (of any dimension) can be split into two triangular numbers (of the same dimension), which gives us the surprising result above.

the image below shows the relationship for a 4×4 multiplication table.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to dan.mackinnon*

The names of the trigonometric ratios tangent and secant are derived from the Latin “to touch” and “to cut” – the tangent to a figure is a line that touches it in one place, where a secant cuts through it in two or more. But how are these geometric terms related to the ratios that bear their names? The answer can be shown using the diagram at the top of the post – a diagram that used to be a standard one in high school trig text books.

Consider the acute angle BAC. Allow |AC| = 1, and construct a unit circle about A that goes through C. Construct a tangent to this circle at C, and extend the segment AB so that it meets this tangent at E. So, the segment CE lies on the tangent while the segment AE lies on the secant of the unit circle formed around BAC. ACE is a new right triangle that contains the original BAC.

The tangent of BAC is BC/AB (opposite/adjacent), but if we now look at the second triangle ACE, we see tht it is also given by (CE/AC)=(CE/1)=CE – the tangent is measured by the segment of the tangent, CE. Similarly, the secant of BAC is given by AC/AB (hypoteneuse/adjacent), but again turning to the second triangle ACE, we see that this is (AC/AB)=(AE/AC)=(AE/1)=AE – and the secant is provided by the length of the secant, AE.

This treatment was taken from the book “Plane Trigonometry and Tables” by G. Wentworth, published in 1903. In some of the texts of this era, the “primary” trigonometric ratios were sin, sec, and tan (rather than sin, cos, and tan), perhaps owing their primacy to constructions like the one described above.

The cosine was considered a secondary trigonometric ratio – its name coming from the phrase “complement’s sine.” Along with the usual ratios, texts often presented several convienience ratios that are now antiquated, such as the versedsine vrsin(x) = 1-cos(x) and the half-versed sine or haversine hvrsn(x)= (1/2)vrsin(x).

The most fundamental trigonometric ratio has the most obscure name. It is generally claimed that the word “sine” comes from Latin word for “bend,” but some have suggested that the word is ultimately derived from the name of the curve formed by the gathering of a toga, or from the Latin word for “bowstring.” In Arithmetic, Algebra, Analysis, Felix Klein states that “sine” represents a Latin mis-translation of an Arabic word, but does not go on to explain its origins any further.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to dan.mackinnon*

In many traditions, Biedermann’s Dictionary of Symbols tells us, “the tree was widely seen as the axis mundi around which the cosmos is organized” and, as mentioned in a previous post, has been widely used to describe the relationship between mathematics and other sciences. Mathematics itself, like many subjects, is often portrayed as a tree whose sub-topics make up branches that continue to grow and bifurcate.

Some recent articles have take a more postmodern perspective on using the tree metaphor to describe mathematics.

Dan Kennedy ‘s “Climbing around on the Tree of Mathematics,” (full text here) and Greg McColm’s “A Metaphor for Mathematics Education” are two recent articles that make arguments by analogy about what mathematics is and how it should be taught. In Kennedy’s argument, mathematics is a tree, while in McColm’s it is a vine – both are organic, growing, and branching. What distinguishes these two uses of metaphor from traditional tree analogies is that both authors are not at all suggesting that we can stand back and survey the structure as a whole and understand how all its parts are related. The ability to provide a comprehensive view of the subject, to make it surveyable, was the raison-d’être of metaphors like the “Tree of Science.” Instead of using the metaphor this way, both authors suggest that we think of ourselves as part of the growing structure – as climbers and gardeners who cannot see the complex organic whole, but who can explore and tend to our small part of it. In these descriptions, natural forms like trees and plants, once metaphors for simplicity and comprehensibility, now provide metaphors for complexity.

Up in the Tree of Mathematics, Kennedy suggests that working mathematicians are labouring at extending its outer branches. This is where the view is best, where the fruit is found, and where the beauty of mathematics can be seen most clearly. School Mathematics is part of the trunk, the solid, oldest, stable part of the tree, and math teachers spend their time helping students climb the trunk, hoping that some may one day reach its outer branches. Unfortunately, the difficulty of the trunk prevents most people from ever climbing beyond it. Kennedy suggests that we should be less concerned with the trunk than with the branches, and that technology can provide a ladder to assist the climb.

McColm’s Mathematical Vine is not mathematics itself, but a structure that clings to the underlying reality of mathematical truth. Mathematics, in this analogy, is like a hidden tower, whose shape can only be seen by looking at the vine that has taken shape around it. Like in Kennedy’s analogy, working mathematicians are the caretakers who help the structure grow. For McColm, this analogy emphasizes the importance of mathematics education – a process of strengthening the vine so that it may continue to grow. Perhaps because his audience is primarily post-secondary researchers, he does not advocate finding shortcuts to “higher” views, but rather suggests that education be promoted through “tending to the vine” – clarifying mathematics and strengthening connections between different branches.

Although they suggest more of a structure at play, rather that a stable unified whole, organic metaphors like those used by McColm and Kennedy continue to suggest a natural unity among the various parts of mathematics. In that sense they are still rooted (or centered), and, although they have somewhat destabilized the tree analogy, they haven’t quite deconstructed it. They have not, for example, gone quite as far as Wittgenstein, who seemed to suggest that metaphors that attempt to link the subjects of mathematics in a defining way like this are misguided. In his view, as described by Ackerman (1988, p. 115):

mathematics is an assemblage of language games, having no sharp and uniform external boundary, with potentially confusing and criss-crossing subdisciplines held together by an internal network of analogous proof techniques.

It is easy to appreciate how some climbers in Kennedy’s trees and McColm’s vines end up like the protagonist in Roz Chast’s cartoon “Falling off the Math Cliff”, where step 1 is “A boy begins his wondrous journey,” and step 8 is “The plummet.”

The images in this post are “Pythagoras Tree” fractals, made using GSP.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to dan.mackinnon*