Month: December 2012

In a remarkable breakthrough in the field of mathematical science, Professor Kyudong Choi from the Department of Mathematical Sciences at UNIST has provided an irrefutable proof that certain spherical vortices exist in a stable state. This discovery holds significant implications for predicting weather anomalies and advancing weather prediction technologies. The research is published in the journal Communications on Pure and Applied Mathematics.

A vortex is a rotating region of fluid, such as air or water, characterized by intense rotation. Common examples include typhoons and tornadoes frequently observed in news reports. Professor Choi’s mathematical proof establishes the stability of specific types of vortex structures that can be encountered in real-world fluid flows.

The study builds upon the foundational Euler equation formulated by Leonhard Euler in 1757 to describe the flow of eddy currents. In 1894, British mathematician M. Hill mathematically demonstrated that a ball-shaped vortex could maintain its shape indefinitely while moving along its axis.

Professor Choi’s research confirms that Hill’s spherical vortex maximizes kinetic energyunder certain conditions through the application of variational methods. By incorporating functional analysis and partial differential equation theory from mathematical analysis, this study extends previous investigations on two-dimensional fluid flows to encompass three-dimensional fluid dynamics with axial symmetry conditions.

One notable feature identified by Hill is the presence of strong upward airflow at the front of the spherical vortex—an attribute often observed in phenomena like typhoons and tornadoes. Professor Choi’s findings serve as a starting point for further studies involving measurements related to residual time associated with these ascending air currents.

“Research on vortex stability has gained international attention,” stated Professor Choi. “And it holds long-term potential for advancements in today’s weather forecasting technology.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to JooHyeon Heo, Ulsan National Institute of Science and Technology

We know the universe is vast, but how do we measure the distances between things? Dave Scrimshaw.

Let’s talk numbers for a moment.

The moon is approximately 384,000 kilometres away, and the sun is approximately 150 million kilometres away. The mean distance between Earth and the sun is known as the “astronomical unit” (AU). Neptune, the most distant planet, then, is 30 AU from the sun.

The nearest stars to Earth are 1,000 times more distant, roughly 4.3 light-years away (one light-year being the distance that light travels in 365.25 days – just under 10 trillion kilometres).

The Milky Way galaxy consists of some 300 billion stars in a spiral-shaped disk roughly 100,000 light-years across.

The Andromeda Galaxy, which can be seen with many home telescopes, is 2.54 million light years away. There are hundreds of billions of galaxies in the observable universe.

At present, the most distant observed galaxy is some 13.2 billion light-years away, formed not long after the Big Bang, 13.75 billion years ago (plus or minus 0.011 billion years).

The scope of the universe was illustrated by the astrophysicist Geraint Lewis in a recent Conversation article.

He noted that, if the entire Milky Way galaxy was represented by a small coin one centimetre across, the Andromeda Galaxy would be another small coin 25 centimetres away.

Going by this scale, the observable universe would extend for 5 kilometres in every direction, encompassing some 300 billion galaxies.

But how can scientists possibly calculate these enormous distances with any confidence?

Parallax

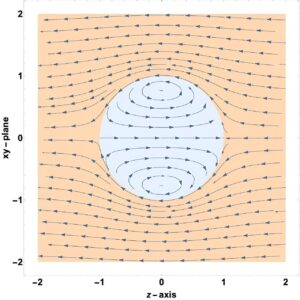
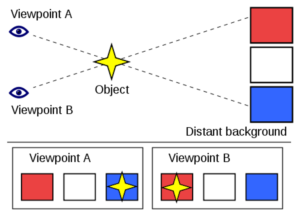
One technique is known as parallax. If you cover one eye and note the position of a nearby object, compared with more distant objects, the nearby object “moves” when you view it with the other eye. This is parallax (see below).

Booyabazooka

The same principle is used in astronomy. As Earth travels around the sun, relatively close stars are observed to move slightly, with respect to other fixed stars that are more distant.

Distance measurements can be made in this way for stars up to about 1,000 light-years away.

Standard candles

For more distant objects such as galaxies, astronomers rely on “standard candles” – bright objects that are known to have a fixed absolute luminosity (brightness).

Since light flux falls off as the square of the distance, by measuring the actual brightness observed on Earth astronomers can calculate the distance.

One type of standard candle, which has been used since the 1920s, is Cepheid variable stars.

Distances determined using this scheme are believed accurate to within about 7% for more nearby galaxies, and 15-20% for the most distant galaxies.

Type Ia supernovas

In recent years scientists have used Type Ia supernovae. These occur in a binary star system when a white dwarf star starts to attract matter from a larger red dwarf star.

As the white dwarf gains more and more matter, it eventually undergoes a runaway nuclear explosion that may briefly outshine an entire galaxy.

Because this process can occur only within a very narrow range of total mass, the absolute luminosity of Type Ia supernovas is very predictable. The uncertainty in these measurements is typically 5%.

In August, worldwide attention was focused on a Type Ia supernova that exploded in the Pinwheel Galaxy (known as M101), a beautiful spiral galaxy located just above the handle of the Big Dipper in the Northern Hemisphere. This is the closest supernova to the earth since the 1987 supernova, which was visible in the Southern Hemisphere.

These and other techniques for astronomical measurements, collectively known as the “cosmic distance ladder”, are described in an excellent Wikipedia article. Such multiple schemes lend an additional measure of reliability to these measurements.

In short, distances to astronomical objects have been measured with a high degree of reliability, using calculations that mostly employ only high-school mathematics.

Thus the overall conclusion of a universe consisting of billions of galaxies, most of them many millions or even billions of light-years away, is now considered beyond reasonable doubt.

Right tools for the job

The kind of distances we’re dealing with above do cause consternation for some since, as we peer millions of light-years into space, we are also peering millions of years into the past.

Some creationists, for instance, have theorised that, in about 4,000 BCE, a Creator placed quadrillions of photons in space en route to Earth, with patterns suggestive of supernova explosions and other events millions of years ago.

Needless to say, most observers reject this notion. Kenneth Miller of Brown University commented, “Their [Creationists’] version of God is one who has filled the universe with so much bogus evidence that the tools of science can give us nothing more than a phony version of reality.”

There are plenty of things in the universe to marvel at, and plenty of tools to help us understand them. That should be enough to keep us engaged for now.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Jonathan Borwein (Jon)*

A surprisingly interesting structure is the extended multiplication table, shown above for the numbers seven to ten. The algorithm for drawing these is straight forward – for an n-extended table, start out as if you were writing a “regular” multiplication table, but extend each row so that it gets as close to, without exceeding, n. Another way to think about it is to write out rows of “skip counting up to n” by i for integers i from 1 to n.

This is called an extended multiplication table since it contains a “traditional” multiplication table inside it. The 12-extended table below contains a traditional 3×3 multiplication table.

It turns out that 1 appears in an extended table once, and prime numbers appear exactly twice (once in the first column, and once in the first row). In general, for a natural number n, how many times does n appear in the n-extended table?

Before looking at that question, you might want to think about finding easier ways to draw the tables. Drawing out these tables by hand can be tedious – a simple program or spreadsheet might be easier. You can use Fathom, for example, to create the table data and draw it in the collections display. Create a slider m and the attributes listed in the table below (click on the image to see a larger version).

Modify the collection display attributes to draw the tables in the collection box. By adding lots of cases and using the slider m to filter out the ones you don’t need, you can vary the size of the table easily.

“how many times does n appear in the n-extended table?”

# of occurrances of n in the n-extended table = # of nodes in the factor lattice Fn

You can also recast both of these questions (how many occurances of n in the n-extended table, and how many nodesin the Fn factor lattice) as a combinatorial “balls in urns” problem.

Consider a set of colored balls where there are m different colours, where there are ki balls of color i, where i ranges from 1 to m. This would give a total number of balls equal to k1+k2+…+km. Suppose you were to distribute these balls in two urns. How many different distributions would there be? Using some counting techniques, you will find that the answer is (k1+1)*(k2+1)*…*(km+1).

How is this connected to the other problems? Consider the prime factorization of the number. For each prime, choose a colour, and for each occurance of the prime in the factorization, add a new ball of that color. For example for 12 = 3*3*2, choose two colours – say blue=3 and red=2. Since 3 occurs twice and 2 occurs once, there should be two blue balls and one red ball. Now consider distributing these balls in two urns. It turns out that you get (2+1)*(1+1) = 6 possibilities. This is the same number of times 12 occurs in the 12-extended table, and the same number of nodes in the 12-factor lattice. The image below shows the 12-extended table, the 12-factor lattice, and the “ball and urn problem” for the numer 12.

For a number n with the prime factorization:

The answer to all three questions is given by:

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to dan.mackinnon*