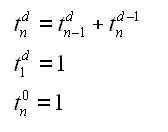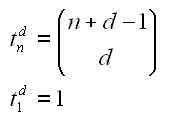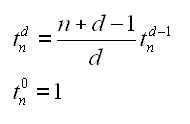There’s a contradiction between classical and quantum theories.
One of the outstanding discoveries made in the early part of the last century was that of the quantum behaviour of the physical world. At very short distances, such as the size of an atom and smaller, the world behaves very differently to the “classical” world we are used to.
Typical of the quantum world is so-called wave-particle duality: particles such as electrons behave sometimes as if they are point particles with a definite position, and sometimes as if they are spread out like waves.
This strange behaviour is not just of theoretical interest, since it is underpins much of our modern technology. It is fundamental to the behaviour of semiconductors in all our electronic devices, the behaviour of nano-materials, and the current rise of quantum computing.
Quantum theory is fundamental. It must govern not just the very small but also the classical realm. That means physicists and mathematicians have had to develop methods not just for understanding new quantum phenomena, but also for replacing classical theories by their quantum analogues.
This is the process of [quantization.](http://en.wikipedia.org/wiki/Quantization_(physics) When we have a finite number of degrees of freedom, such as for a finite collection of particles, although the quantum behaviour is often counter-intuitive, we have a well-developed mathematical machinery to handle this quantization called quantum mechanics.
This is well understood physically and mathematically. But when we move to study the electric and magnetic fields where we have an infinite number of degrees of freedom, the situation is much more complicated. With the development of so-called quantum field theory, a quantum theory for fields, physics has made progress that mathematically we do not completely understand.
What’s the problem?
Many field theories fall into a class called gauge field theories, where a particular collection of symmetries, called the gauge group, acts on the fields and particles. In the case that these symmetries all commute, so-called abelian gauge theories, we have a reasonable understanding of the quantization.
This includes the case of the electromagnetic field, quantum electrodynamics, for which the theory makes impressively accurate predictions.
The first example of a non-abelian theory that arose historically is the theory of the electro-weak interaction, which requires a mechanism to make the predicted particles massive as we observe them in nature. This involves the so-called Higgs boson, which is currently being searched for with the Large Hadron Collider (LHC) at CERN.
The notable feature of this theory for our present discussion is that the Higgs mechanism is classical and carries over to the quantum theory under the quantization process.
The case of interest in the Millennium Problem “Yang-Mills theory and Mass-Gap” is Yang-Mills gauge theory, a non-abelian theory which we expect to describe quarks and the strong force that binds the nucleus and powers the sun. Here we encounter a contradiction between the classical and quantum theories.
The classical theory predicts massless particles and long-range forces. The quantum theory has to match the real world with short-range forces and massive particles. Physicists expect various mathematical properties such as the “mass gap” and “asymptotic freedom” to explain the non-existence of massless particles in observations of the strong interactions.
As these properties are not visible in the classical theory and arise only in the quantum theory, understanding them means we need a rigorous approach to “quantum Yang-Mills theory”. Currently we do not have the mathematics to do this, although various approximations and simplifications can be done which suggest the quantum theory has the required properties.
The Millennium Problem seeks to establish by rigorous mathematics the existence of the “mass gap” – that is, the non-existence of massless particles in Yang-Mills theory. The solution of the problem would involve an approach to quantum field theory in four dimensions that is sophisticated enough to explain at least this feature of quantum non-abelian Yang-Mills gauge theory.
Doing the maths
Clearly this is of interest to physicists, but why is it of importance to mathematicians? It has become apparent in the last few decades that the tools that physicists have developed for doing quantum field theory, in particular path integrals, make precise predictions about geometry and topology, particularly in low dimensions.
But we don’t know mathematically what a path integral is, except in very simple cases. It is as if we are in a pre-Newtonian world – certain calculations can be done with certain tricks but Newton hasn’t developed calculus for us yet.
Analogously, there are calculations in geometry and topology that can be done non-rigorously using methods developed by physicists in quantum field theory which give the right answers. This suggests that there is a set of powerful techniques waiting to be discovered.
A solution to this Millennium Problem would shed light on what these new techniques are.
For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to Michael Murray*