Month: April 2009

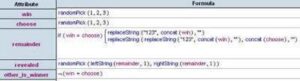
Some students get their first look at manipulating equations when they learn how to convert a repeating decimal to its corresponding fraction (rational numbers yield terminating decimals, or non-terminating repeating decimals). Playing with fractions and decimals is always good in itself, but there are also two nice side-benefits to this simple calculation: first, you can see the surprising result that  0.999… = 1, and second, it helps answer the question ‘which fractions lead  to terminating decimals, and which lead to repeating decimals?’ Better still, it leads to other questions.

1. The calculation – turning decimals into fractions

A repeating decimal like 0.633633… can be written as a fraction by writing out the equation x =  0.633633…, and then manipulating it so that the infinitely long repeated parts get eliminated. The manipulation is done by multiplying the equation by the right power of 10 to shift the digits, and then subtracting off the original equation.

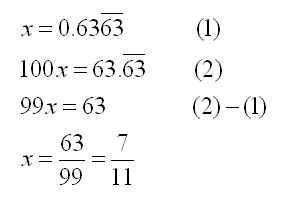
Perhaps you have a more complicated repeating decimal that you want to fractionalize. The procedure remains essentially the same: obtain two equations that have the same “decimal part” that can be eliminated by subtracting. You might have to shift twice in order to accomplish this. Here is an example:

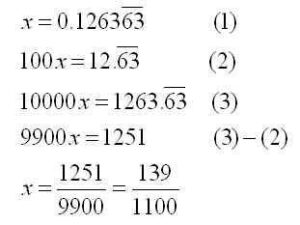
2. Showing that 0.999… = 1

This school mathematics result has been made into a popular topic of discussion on the Internet. Try doing a search on “0.999 = 1”, and see what you find.

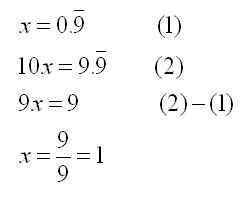
3. Which fractions terminate, and which keep going?

A fraction can sometimes give us a terminating decimal, and sometimes a repeating decimal. It is reasonable to wonder what kind of fractions lead to each kind of decimal.

Thinking about the procedure above might give you an idea for how to think about this question.

If we have a situation where a fraction x = p/q is a terminating decimal, it means that there must be some power of 10, say 10^n, that if we multiply x by  this power we can completely eliminate the decimal (i.e. multiplying by 10^n gives us an integer). This could only happen if the denominator q divides 10^n. This would require q to be of the form (2^m)(5^k), where the exponents m and k are non negative integers (possibly zero), and n = max(m, k).

So, a fraction p/q terminates if and only if the denominator is of the form (2^m)(5^k). Consequently, fractions such as 1/2, 3/5, 9/25, 7/8, 3/200, are all terminating, and, for example, any fraction of the form 1/p where p is a prime that is not 2 or 5, will be non-terminating and repeating.

It is reasonable to ask questions about how long the decimals or their repeating parts can be. For a non-terminating repeating decimal, questions about the length of the repeating part are harder to answer.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to dan.mackinnon*

See a vertical stripe, what you are seeing is a run of repeated digits, like 7777, 00000, or 222.

One occurs in the top left:

Sequences like this used to be important examples in motivating discussions about the law of the excluded middle. Statements like: ‘the decimal expansion of pi contains the sequence 7777’, according to the law of the excluded middle, are either true or false. But when you are discussing something that has never been calculated, and that might never be calculated, suggests (to constructivists), that the statement may be neither true or false, and that the sequence 7777 may be somewhat like Schrodinger’s cat, neither existing nor not existing.

Now that the digits of pi have been calculated to astounding lengths, and that mathematics exists to uncover the properties of the pi digit sequence, the expansion of pi is no longer an ideal candidate for constructivist thought experiments. Even some exotic questions about the decimal expansion of pi, like the convergence of the brouwer-heyting sequence, have been resolved. Questions about the expansion of pi that illustrate constructivist problems can still be formulated, but they need to be more complicated than they used to be.

Still, I decided to look more closely at this little sequence that occurs (relatively) early on in the pi expansion. The stripe in the pi colour map mentioned above corresponds to the sequence 999999 beginning at digit 763 and ending at digit 768. This was observed in a set of the first 2281 digits of pi.

I decided to push the software a bit further, and load 10000 digits of pi into the document.  (A file with the first 10000 digits of pi formatted for Fathom or TinkerPlots is here.) The plot below shows the digits with 9 in black and all other digits blanked out – dots are single occurrences of a 9, while vertical stripes are runs of repeated 9s.

Using Tinkerplots’ runLength function we can see how frequent runs of various lengths are, and easily identify the longer ones.

Even with 10000 digits, the 999999 sequence at digit 763 was still the longest sequence of repeated digits. The other runner-up sequences in this first 10000 digits are, two instances of 2222, a single run of 8888, and four distinct occurrences of 7777.

The plot at the bottom of this post shows the distribution of even and odd digits in the decimal expansion of pi’s first 10000 digits, and was inspired by a similar plot from Wolfram Math World.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to dan.mackinnon*

Brian Hayes recently provided some evidence that there are still many out there who are confounded by the Monty Hall problem.

The Monty Hall problem, perhaps the best-known counter-intuitive probability problem, gets a nice treatment in Jeffery Rosenthal’s Struck by Lightning: The Curious World of Probabilities, and is also explained well (perhaps better) in Mark Haddon’s novel The Curious Incident of the Dog in the Night-time. Professor Rosenthal has some further Monty Hall explanations here.

I just found an alternate version of the problem in Martin Gardner’s The Second Scientific American Book of Mathematical Puzzles and Diversions (published also by Penguin in a slightly different form as More Mathematical Puzzles and Diversions). In the chapter “Probability and Ambiguity” (chapter 19 in both versions of the book), Gardner describes the problem of the three prisoners. Here is a condensed description of the problem:

Three prisoners, A, B, and C are in separate cells and sentenced to death. The governor has selected one of them at random to be pardoned. Finding out that one is to be released, prisoner A begs the warden to let him know the identity of one of the others who is going to be executed. “If B is to be pardoned, give me C’s name. If C is to be pardoned, give me B’s name. And if I’m to be pardoned, flip a coin to decide whether to name B or C.”

The warden tells A that B is to be executed. Prisoner A is pleased because he believes that his probability of surviving has gone up from 1/3 to 1/2. Prisoner A secretly tells C the news, who is also happy to hear it, believing that his chance of survival has also risen to 1/2.

Are A and C correct? No. Prisoner A’s probability of surviving is still 1/3, but prisoner C’s probability of receiving the pardon is 2/3.

It is reasonably easy to see that the 3 prisoners problem is the same as the Monty Hall problem. Seeing the problem in this different formulation might help those who continue to struggle with it.

It is a nice activity to simulate both the 3 prisoners problem and the Monty Hall problem in Fathom – try it and confirm the surprising results that the “second prisoner” is pardoned 2/3 of the time, and that 2/3 of the time, the winning curtain is not the one you selected first.

There are many, many, ways to write these simulations. Here are the attributes and formulas for a Fathom implementation of the three prisoners:

The table below (click on it to see a larger version) shows a separate simulation for the Monty Hall problem. Here we are assuming three curtains “1”, “2”, and “3”, one of which has a prize behind it. You pick one, and then Monty reveals the contents behind one of the other curtains (the curtain with the prize behind it is not shown). In the game, you have the option of switching your choice for the curtain that has not been revealed.

After creating the attributes, you can “run the simulation” by adding data to the collection (Collection->New Cases…), the more the better.

Incidentally, Gardner’s use of A, B, and C reminds me of Stephen Leacock’s “A, B, and C: The Human Element in Mathematics.”

Addendum

A quick search shows that the connection between the Monty Hall problem and the Three Prisoners is well known (see the wikipedia entries on Monty Hall and the Three Prisoners), and that both are alternate formulations of an older problem, known as Bertrand’s box paradox.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to dan.mackinnon*