Month: October 2008

Phyllotaxis is a term used for the patterns that emerge in the growth of plants. Spiral phyllotaxis is observed in the heads of sunflowers, in pine-cones and pineapples, and in a variety of other plants.

Phyllotaxis is a popular topic in mathematics recreation – it’s interesting in its own right and also related to other perennial favourites, Fibonacci numbers and the golden ratio.

The article Modeling Spiral Growth in a GSP Environment describes how to model phyllotaxis-like patterns in GSP. Although GSP works reasonably well, TinkerPlots or Fathom environments seem to be better suited to capturing this particular model – they make the formulas more explicit and easy to manipulate, and they allow for the data generated to be viewed in a variety of ways. The images above were created by porting this model to TinkerPlots.

As the article suggests, experimenting with the the angle between successive seeds allows you to see different resulting patterns – angles that are multiples of rational numbers create patterns of rays while irrational numbers (actually approximate values) give spirals, or spiral/ray combinations (the rays form as the approximation gets more “rational”). A good choice for approximating actual phyllotaxis patterns is to use tau = (1+sqrt(5))/2 in your angle. Here is a listing for the attributes required to generate the pattern in TP or Fathom. The graph/plot is simply the x attribute on the horizontal and the y attribute on the vertical (in TP these need to be fully separated).

n = caseIndex
base_angle = pi*(1+sqrt(5))
r = sqrt(n)
theta = n*base_angle
x = r*cos(theta)
y = r*sin(theta)

The images shown in this post use a collection of 500 cases or “seeds”. The base angle is 2pi*tau, and the actual angle for a given seed is a multiple of this base angle.

The model is nice looking and easy to build, but it models only the end result of the growth process, not the process itself. It winds new seeds around the outer edge based on a pre-determined angle. A better model would be one that mirrors what is understood to be the underlying phonomena – new seeds are added to the center and old seeds are pushed out following a set of rules. Under this dynamic method, the angles and spirals are an emergent aspect of the system, rather than the explicit result. This website describes how such a dynamical system could be modeled.

Although the Fathom/TP model does not model the dynamical system that underlies phyllotaxis, it’s fun to play with in its own right. You can manually alter the base_angle attribute as suggested by the GSP article. If you add a parameter (a slider) to help you vary the angle, you can obtain a whole family of spiral/ray patterns whose properties you could take a closer look at. Different combinations of angles and sliders will give you various levels of control over the image.

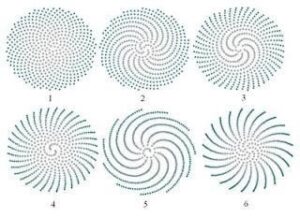
For example, change the formula for base_angle to base_angle = pi*(1+sqrt(5))*base, and create a slider “base”. The image below shows the spirals obtained for base = 1…6.

Update: Here is an example of how to draw spirals like this in R.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to dan.mackinnon*

The humble pigeon mightn’t look smart, but it’s no bird-brain.

We humans have long been interested in defining the abilities that set us apart from other species. Along with capabilities such as language, the ability to recognise and manipulate numbers (“numerical competence”) has long been seen as a hallmark of human cognition.

In reality, a number of animal species are numerically competent and according to new research from psychologists at the University of Otago in New Zealand, the humble pigeon could be one such species.

Damian Scarf, Harlene Hayne and Michael Colombo found that pigeons possess far greater numerical abilities than was previously thought, actually putting them on par with primates.

More on pigeons in a moment, but first: why would non-human animals even need to be numerically competent? Would they encounter numerical problems in day-to-day life?

In fact, there are many reports indicating that number is an important factor in the way many species behave.

Brown cowbirds are nest parasites – they lay their eggs in the nests of “host” species; species that are then landed with the job of raising a young cowbird.

Cowbirds are sensitive to the number of eggs in the host nest, preferring to lay in nests with three host eggs rather than one. This presumably ensures the host parent is close to the end of laying a complete clutch and will begin incubating shortly after the parasite egg has been added.

Crows identify individuals by the number of caw sounds in their vocalisations, while lionesses appear to evaluate the risk of approaching intruder lions based on how many individuals they hear roaring.

But numerical competence is about more than an ability to count. In fact, it’s three distinct abilities:

• the “cardinal” aspect: the ability to evaluate quantity (eg. counting the number of eggs already in a nest)
• the “ordinal” aspect: the ability to put an arbitrary collection of items in their correct order or rank (eg. ordering a list of animals based on the number of legs they have, or ordering the letters of the alphabet)
• the “symbolic” aspect: the ability to symbolically represent a given numerical quantity (eg. the number “3” or the word “three” are symbols that represent the quantity 3).

We know that humans are capable of all three aspects of numerical competence, but what about other animals?

For a start, we already know that the cowbird, lion and crow possess the cardinal aspect of numerical competency – they are all able to count. Pigeons possess the cardinal aspect too (as was reported as early as 1941) as do several other vertebrate and invertebrate species.

And in 1998, Elizabeth Brannon and Herbert Terrace showed that rhesus monkeys have the ability to order arrays of objects according to the number of items contained within these arrays. After learning to order sets of one, two and three items, the monkeys were able to order any three sets containing from one to nine items.

This discovery represented a clear progression in complexity, since ranking according to numerical quantity is an abstract ability – the ordinal aspect.

The new research by Scarf, Hayne and Colombo – which was published in Science in late December – has pushed, even further, our understanding of numerical abilities in the animal kingdom.

So what did they do?

Well, first they trained pigeons to peck three “stimulus arrays” – collections of objects on a touch screen. These arrays contained one, two or three objects and to receive a reward, the pigeon had to peck the arrays in order – the array with one object first, the array with two objects second, the array with three objects third.

Once this basic requirement was learned, the pigeons were presented with different object sets – one set containing arrays with one to three objects, and sets containing up to nine objects.

Having been presented with these novel object sets, the pigeons were once again required to peck the sets in ascending order. Pigeons solved the task successfully, even though they had never been trained with arrays containing more than three items.

A pigeon taking part in the University of Otago experiment.

In fact, they performed on par with rhesus monkeys, demonstrating that both pigeons and monkeys are able to identify and order the numbers from one to nine. This is significant because it shows these complex numerical abilities are not confined to the primates (and that pigeons are smarter than many people think!)

So if non-human animals possess the cardinal and ordinal aspects of numerical competency, that means it’s the symbolic representation of numbers that makes humans unique, right?

As it turns out, no.

It’s been shown that red wood ants (Formica polyctena) can not only count up to several tens (20, 30 etc.), but can also communicate this numerical information to their brethren.

It would seem, therefore, that not even the symbolic representation of numerical information is specific to humans.

Of course, we still have much more to discover and understand within this fascinating field of research. In the meantime, you might want to think twice before dismissing pigeons as “stupid birds”.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to David Guez and Andrea S. Griffin*