
During a lunch in the summer of 1950, physicists Enrico Fermi, Edward Teller and Herbert York were chatting about a recent New Yorker cartoon depicting aliens abducting trash cans in flying saucers. Suddenly, Fermi blurted out, “Where is everybody?”
He reasoned: “Since there are likely many other technological civilisations in the Milky Way galaxy, and since in a few tens of thousands of years at most they could have explored or even colonised many distant planets, why don’t we see any evidence of even a single extraterrestrial civilisation?”
This has come to be known as Fermi’s Paradox.
Clearly the question of whether other civilisations exist is one of the most important questions of modern science. Any discovery of a distant civilisation – say by analysis of microwave data – would rank as among the most far-reaching of all scientific discoveries.
Drake equation
At a 1960 conference regarding extraterrestrial intelligence, Frank Drake (1930 —) sketched out what is now the Drake equation, estimating the number of civilisations in the Milky Way with which we could potentially communicate:
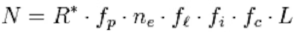
where
N = number of civilisations in our galaxy that can communicate.
R* = average rate of star formation per year in galaxy.
fp = fraction of those stars that have planets.
ne = average number of planets that can support life, per star that has planets.
fl = fraction of the above that eventually develop life.
fi = fraction of the above that eventually develop intelligent life.
fc = fraction of civilisations that develop technology that signals existence into space.
L = length of time such civilisations release detectable signals into space.
The result? Drake estimated ten such civilisations were out there somewhere in the Milky Way.
This analysis, led to the Search for Extraterrestrial Intelligence (SETI) project, looking for radio transmissions in a region of the electromagnetic spectrum thought best suited for interstellar communication.
But after 50 years of searching, using increasingly powerful equipment, nothing has been found.
So where is everybody?
Proposed solutions to Fermi’s paradox
Numerous scientists have examined Fermi’s paradox and proposed solutions. The following is a list of some of the proposed solutions, and common rejoinders:
- Such civilisations are here, or are observing us, but are under orders not to disclose their existence.
Common rejoinder: This explanation (known as the “zookeeper’s theory”) is preferred by some scientists including, for instance, the late Carl Sagan. But it falls prey to the fact that it would take just one member of an extraterrestrial society to break the pact of silence – and this would seem inevitable.
- Such civilisations have been here and planted seeds of life, or perhaps left messages in DNA.
Common rejoinder: The notion that life began on Earth from bacterial spores or the like that originated elsewhere, known as the “panspermia theory”, only pushes the origin of life problem to some other star system – scientists see no evidence in DNA sequences of anything artificial.
- Such civilisations exist but are too far away.
Common rejoinder: A sufficiently advanced civilisation could send probes to distant stars, which could scout out suitable planets, land and construct copies of themselves, using the latest software beamed from home.
So, the entire Milky Way galaxy could be explored within, at most, a few million years.
- Such civilisations exist but have lost interest in interstellar engagement.
Common rejoinder: As with the zookeeper theory, this would require each civilisation to forever lack interest in communication and transportation – and someone would most likely break the pact of silence.
- Such civilisations are calling, but we don’t recognise the signal.
Common rejoinder: This explanation doesn’t apply to signals sent with the direct purpose of communicating to nascent technological societies. Again, it is hard to see how a galactic society could enforce a global ban.
- Civilisations invariably self-destruct.
Common rejoinder: This contingency is already figured into the Drake equation (the L term, above). In any event, we have survived at least 100 years of technological adolescence, and have managed (until now) not to destroy ourselves in a nuclear or biological apocalypse.
Relatively soon we will colonise the moon and Mars, and our long-term survival will no longer rely on Earth.
- Earth is a unique planet in fostering long-lived ecosystems resulting in intelligent life.
Common rejoinder: Perhaps, but the latest studies, in particular the detections of extrasolar planets point in the opposite direction. Environments like ours appear quite common.
- We are alone in the Milky Way galaxy. Some scientists further conclude we are alone in the entire observable universe.
Common rejoinder: This conclusion flies in the face of the “principle of mediocrity,” namely the presumption, popular since the time of Copernicus, that there’s nothing special about human society or environment.
Stephen Webb’s 2002 book If the Universe Is Teeming with Aliens … Where is Everybody, provides numerous other proposed solutions and rejoinders.
Two of Drake’s key terms – fp (the fraction of stars that have planets) and ne (the average number of planets that can support life, per star that has planets) are subject to measurement.
Scientists once thought stable planetary systems and Earth-like planets were a rarity. But recent evidence suggests otherwise.
Thanks to Kepler and other projects, these two terms have been found to have reasonable values, although not quite as optimistic as Drake and his colleagues first estimated.
With every new research finding in the area of extrasolar planets and possible extraterrestrial living organisms, the mystery of Fermi’s paradox deepens.
“Where is everybody?” is a question that now carries even greater resonance.
For more such insights, log into our website https://international-maths-challenge.com
Credit of the article given to Jonathan Borwein (Jon), University of Newcastle and David H. Bailey, University of California, Davis.


