![]()
Chapter 3 of Hardy & Wright’s An Introduction to the Theory of Numbers involves Farey sequences – which, in addition to showing up in serious number theory books, are an interesting, accessible, and popular topic in recreational mathematics.
Since I am a committed constructivist (in at least a few senses of the word) I thought it would be nice to come up with an activity with Farey sequences that could be carried out without too much advance discussion about what they are. What I came up with is a Fathom activity that starts with some simple but odd looking data that allows you to construct some very interesting plots and displays. The idea is that you will get a feel for what a Farey sequence is by using the data to build the sequence and by looking at the results from different perspectives.
Step 1. Import some data
Here is the data to import into Fathom. It should create 33 cases with two attributes n, and d.
n d
0 1
1 10
1 9
1 8
1 7
1 6
1 5
2 9
1 4
2 7
3 10
1 3
3 8
2 5
3 7
4 9
1 2
5 9
4 7
3 5
5 8
2 3
7 10
5 7
3 4
7 9
4 5
5 6
6 7
7 8
8 9
9 10
1 1
Step 2. Add some more attributes
After importing this data, you should create the following attributes
i = caseIndex
q = n/d
dist = q – prev(q)
mediant = (n+prev(n))/(d+prev(d))
d_mediant = mediant – prev(mediant)
disp = concat(n,”/”,d)
The meaning of the “mediant” attributes will become clearer after you read about Farey sequences.
Step 3. Explore some plots
Plots you could try creating are:
- A) n on the y axis and d on the x axis.
- B) dist on y, i on x (a filter of i>1 makes sense here)
- C) d_mediant on y, i on x (a filter of i>2 makes sense here)
- D) mediant on y, q on x (adding a function y=x makes sense here)
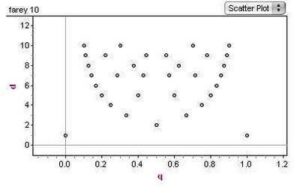
- E) d on y, q on x
- F) dist on y, q on x
- H) q on x with no other attributes
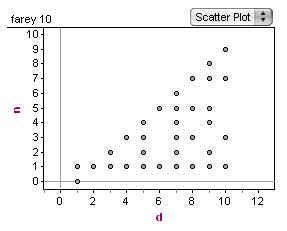
While creating these plots, you should be thinking about describing the sequence that the cases represent. What kinds of numbers are they, what values do they have (do they lie in a certain interval?), how close are they to one another?
Step 4. Create a nice display
One of the more visually interesting thing you can do with the Farey sequence is to display its associated Ford circles. This can be done by adding two new sliders and by editing the display settings for the collection.
Add the sliders “scale” and “shift,” and give them these initial values:
scale = 400
shift = 150
Now on the collection inspector, click on the Display tab, and edit the formulas for these attributes
x= q*scale +shift
y = scale/(2*d^2)
image = blueCircleIcon
width = scale/(d^2)
height = scale/(d^2)
caption = “”
If you pull open the display, you will see the initial iterations of a fractal pattern known as the Ford Circles that are generated by the Farey sequence. Here is what it should look like:

For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to dan.mackinnon*
