Month: July 2004

Number theory, the study of the properties of positive integers, is perhaps the purest form of mathematics. At first sight, it may seem far too abstract to apply to the natural world. In fact, the influential American number theorist Leonard Dickson wrote, “Thank God that number theory is unsullied by any application.”

And yet, again and again, number theory finds unexpected applications in science and engineering, from leaf angles that (almost) universally follow the Fibonacci sequence, to modern encryption techniques based on factoring prime numbers. Now, researchers have demonstrated an unexpected link between number theory and evolutionary genetics. Their work is published in the Journal of The Royal Society Interface.

Specifically, the team of researchers (from Oxford, Harvard, Cambridge, GUST, MIT, Imperial, and the Alan Turing Institute) have discovered a deep connection between the sums-of-digits function from number theory and a key quantity in genetics, the phenotype mutational robustness. This quality is defined as the average probability that a point mutation does not change a phenotype (a characteristic of an organism).

The discovery may have important implications for evolutionary genetics. Many genetic mutations are neutral, meaning that they can slowly accumulate over time without affecting the viability of the phenotype. These neutral mutations cause genome sequences to change at a steady rate over time. Because this rate is known, scientists can compare the percentage difference in the sequence between two organisms and infer when their latest common ancestor lived.

But the existence of these neutral mutations posed an important question: what fraction of mutations to a sequence are neutral? This property, called the phenotype mutational robustness, defines the average amount of mutations that can occur across all sequences without affecting the phenotype.

Professor Ard Louis from the University of Oxford, who led the study, said, “We have known for some time that many biological systems exhibit remarkably high phenotype robustness, without which evolution would not be possible. But we didn’t know what the absolute maximal robustness possible would be, or if there even was a maximum.”

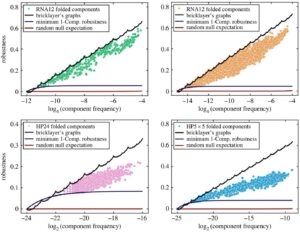
It is precisely this question that the team has answered. They proved that the maximum robustness is proportional to the logarithm of the fraction of all possible sequences that map to a phenotype, with a correction which is given by the sums of digits function s_k(n), defined as the sum of the digits of a natural number n in base k. For example, for n = 123 in base 10, the digit sum would be s₁₀(123) = 1 + 2 + 3 = 6.

Another surprise was that the maximum robustness also turns out to be related to the famous Tagaki function, a bizarre function that is continuous everywhere, but differentiable nowhere. This fractal function is also called the blancmange curve, because it looks like the French dessert.

First author Dr. Vaibhav Mohanty (Harvard Medical School) added, “What is most surprising is that we found clear evidence in the mapping from sequences to RNA secondary structures that nature in some cases achieves the exact maximum robustness bound. It’s as if biology knows about the fractal sums-of-digits function.”

Professor Ard Louis added, “The beauty of number theory lies not only in the abstract relationships it uncovers between integers, but also in the deep mathematical structures it illuminates in our natural world. We believe that many intriguing new links between number theory and genetics will be found in the future.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to University of Oxford

The Fourier transform is one of the most fundamental concepts in the information sciences. It’s a method for representing an irregular signal — such as the voltage fluctuations in the wire that connects an MP3 player to a loudspeaker — as a combination of pure frequencies. It’s universal in signal processing, but it can also be used to compress image and audio files, solve differential equations and price stock options, among other things.

The reason the Fourier transform is so prevalent is an algorithm called the fast Fourier transform (FFT), devised in the mid-1960s, which made it practical to calculate Fourier transforms on the fly. Ever since the FFT was proposed, however, people have wondered whether an even faster algorithm could be found.

At the Association for Computing Machinery’s Symposium on Discrete Algorithms (SODA) this week, a group of MIT researchers will present a new algorithm that, in a large range of practically important cases, improves on the fast Fourier transform. Under some circumstances, the improvement can be dramatic — a tenfold increase in speed. The new algorithm could be particularly useful for image compression, enabling, say, smartphones to wirelessly transmit large video files without draining their batteries or consuming their monthly bandwidth allotments.

Like the FFT, the new algorithm works on digital signals. A digital signal is just a series of numbers — discrete samples of an analog signal, such as the sound of a musical instrument. The FFT takes a digital signal containing a certain number of samples and expresses it as the weighted sum of an equivalent number of frequencies.

“Weighted” means that some of those frequencies count more toward the total than others. Indeed, many of the frequencies may have such low weights that they can be safely disregarded. That’s why the Fourier transform is useful for compression. An eight-by-eight block of pixels can be thought of as a 64-sample signal, and thus as the sum of 64 different frequencies. But as the researchers point out in their new paper, empirical studies show that on average, 57 of those frequencies can be discarded with minimal loss of image quality.

Heavyweight division

Signals whose Fourier transforms include a relatively small number of heavily weighted frequencies are called “sparse.” The new algorithm determines the weights of a signal’s most heavily weighted frequencies; the sparser the signal, the greater the speedup the algorithm provides. Indeed, if the signal is sparse enough, the algorithm can simply sample it randomly rather than reading it in its entirety.

“In nature, most of the normal signals are sparse,” says Dina Katabi, one of the developers of the new algorithm. Consider, for instance, a recording of a piece of chamber music: The composite signal consists of only a few instruments each playing only one note at a time. A recording, on the other hand, of all possible instruments each playing all possible notes at once wouldn’t be sparse — but neither would it be a signal that anyone cares about.

The new algorithm — which associate professor Katabi and professor Piotr Indyk, both of MIT’s Computer Science and Artificial Intelligence Laboratory (CSAIL), developed together with their students Eric Price and Haitham Hassanieh — relies on two key ideas. The first is to divide a signal into narrower slices of bandwidth, sized so that a slice will generally contain only one frequency with a heavy weight.

In signal processing, the basic tool for isolating particular frequencies is a filter. But filters tend to have blurry boundaries: One range of frequencies will pass through the filter more or less intact; frequencies just outside that range will be somewhat attenuated; frequencies outside that range will be attenuated still more; and so on, until you reach the frequencies that are filtered out almost perfectly.

If it so happens that the one frequency with a heavy weight is at the edge of the filter, however, it could end up so attenuated that it can’t be identified. So the researchers’ first contribution was to find a computationally efficient way to combine filters so that they overlap, ensuring that no frequencies inside the target range will be unduly attenuated, but that the boundaries between slices of spectrum are still fairly sharp.

Zeroing in

Once they’ve isolated a slice of spectrum, however, the researchers still have to identify the most heavily weighted frequency in that slice. In the SODA paper, they do this by repeatedly cutting the slice of spectrum into smaller pieces and keeping only those in which most of the signal power is concentrated. But in an as-yet-unpublished paper, they describe a much more efficient technique, which borrows a signal-processing strategy from 4G cellular networks. Frequencies are generally represented as up-and-down squiggles, but they can also be though of as oscillations; by sampling the same slice of bandwidth at different times, the researchers can determine where the dominant frequency is in its oscillatory cycle.

Two University of Michigan researchers — Anna Gilbert, a professor of mathematics, and Martin Strauss, an associate professor of mathematics and of electrical engineering and computer science — had previously proposed an algorithm that improved on the FFT for very sparse signals. “Some of the previous work, including my own with Anna Gilbert and so on, would improve upon the fast Fourier transform algorithm, but only if the sparsity k” — the number of heavily weighted frequencies — “was considerably smaller than the input size n,” Strauss says. The MIT researchers’ algorithm, however, “greatly expands the number of circumstances where one can beat the traditional FFT,” Strauss says. “Even if that number k is starting to get close to n — to all of them being important — this algorithm still gives some improvement over FFT.”

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Larry Hardesty, Massachusetts Institute of Technology