Month: July 2003

Some students get their first look at manipulating equations when they learn how to convert a repeating decimal to its corresponding fraction (rational numbers yield terminating decimals, or non-terminating repeating decimals). Playing with fractions and decimals is always good in itself, but there are also two nice side-benefits to this simple calculation: first, you can see the surprising result that  0.999… = 1, and second, it helps answer the question ‘which fractions lead  to terminating decimals, and which lead to repeating decimals?’ Better still, it leads to other questions.

1. The calculation – turning decimals into fractions

A repeating decimal like 0.633633… can be written as a fraction by writing out the equation x =  0.633633…, and then manipulating it so that the infinitely long repeated parts get eliminated. The manipulation is done by multiplying the equation by the right power of 10 to shift the digits, and then subtracting off the original equation.

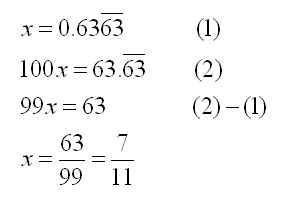
Perhaps you have a more complicated repeating decimal that you want to fractionalize. The procedure remains essentially the same: obtain two equations that have the same “decimal part” that can be eliminated by subtracting. You might have to shift twice in order to accomplish this. Here is an example:

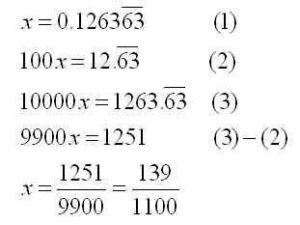
2. Showing that 0.999… = 1

This school mathematics result has been made into a popular topic of discussion on the Internet. Try doing a search on “0.999 = 1”, and see what you find.

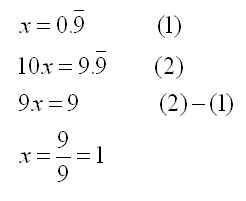
3. Which fractions terminate, and which keep going?

A fraction can sometimes give us a terminating decimal, and sometimes a repeating decimal. It is reasonable to wonder what kind of fractions lead to each kind of decimal.

Thinking about the procedure above might give you an idea for how to think about this question.

If we have a situation where a fraction x = p/q is a terminating decimal, it means that there must be some power of 10, say 10^n, that if we multiply x by  this power we can completely eliminate the decimal (i.e. multiplying by 10^n gives us an integer). This could only happen if the denominator q divides 10^n. This would require q to be of the form (2^m)(5^k), where the exponents m and k are non negative integers (possibly zero), and n = max(m, k).

So, a fraction p/q terminates if and only if the denominator is of the form (2^m)(5^k). Consequently, fractions such as 1/2, 3/5, 9/25, 7/8, 3/200, are all terminating, and, for example, any fraction of the form 1/p where p is a prime that is not 2 or 5, will be non-terminating and repeating.

It is reasonable to ask questions about how long the decimals or their repeating parts can be. For a non-terminating repeating decimal, questions about the length of the repeating part are harder to answer.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to dan.mackinnon*

Maths tells us the best way to cover a surface with copies of a shape – even when it comes to jigsaw puzzles, says Katie Steckles.

WHAT do a bathroom wall, a honeycomb and a jigsaw puzzle have in common? Obviously, the answer is mathematics.

If you are trying to cover a surface with copies of a shape – say, for example, you are tiling a bathroom – you ideally want a shape like a square or rectangle. They will cover the whole surface with no gaps, which is why these boring shapes get used as wall tiles so often.

But if your shapes don’t fit together exactly, you can still try to get the best coverage possible by arranging them in an efficient way.

Imagine trying to cover a surface with circular coins. The roundness of the circles means there will be gaps between them. For example, we could use a square grid, placing the coins on the intersections. This will cover about 78.5 per cent of the area.

But this isn’t the most efficient way: in 1773, mathematician Joseph-Louis Lagrange showed that the optimal arrangement of circles involves a hexagonal grid, like the cells in a regular honeycomb – neat rows where each circle sits nestled between the two below it.

In this situation, the circles will cover around 90.7 per cent of the space, which is the best you can achieve with this shape. If you ever need to cover a surface with same-size circles, or pack identical round things into a tray, the hexagon arrangement is the way to go.

But this isn’t just useful knowledge if you are a bee: a recent research paper used this hexagonal arrangement to figure out the optimal size table for working a jigsaw puzzle. The researchers calculated how much space would be needed to lay out the pieces of an unsolved jigsaw puzzle, relative to the solved version. Puzzle pieces aren’t circular, but they can be in any orientation and the tabs sticking out stop them from moving closer together, so each takes up a theoretically circular space on the table.

By comparing the size of the central rectangular section of the jigsaw piece to the area it would take up in the hexagonal arrangement, the paper concluded that an unsolved puzzle takes up around 1.73 times as much space.

This is the square root of three (√3), a number with close connections to the regular hexagon – one with a side length of 1 will have a height of √3. Consequently, there is also a √3 in the formula for the hexagon’s area, which is 3/2 × √3 × s², where s is the length of a side. This is partly why it pops out, after some fortuitous cancellation, as the answer here.

So if you know the dimensions of a completed jigsaw puzzle, you can figure out what size table you need to lay out all the pieces: multiply the width and height, then multiply that by 1.73. For this ingenious insight, we can thank the bees.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Katie Steckles*