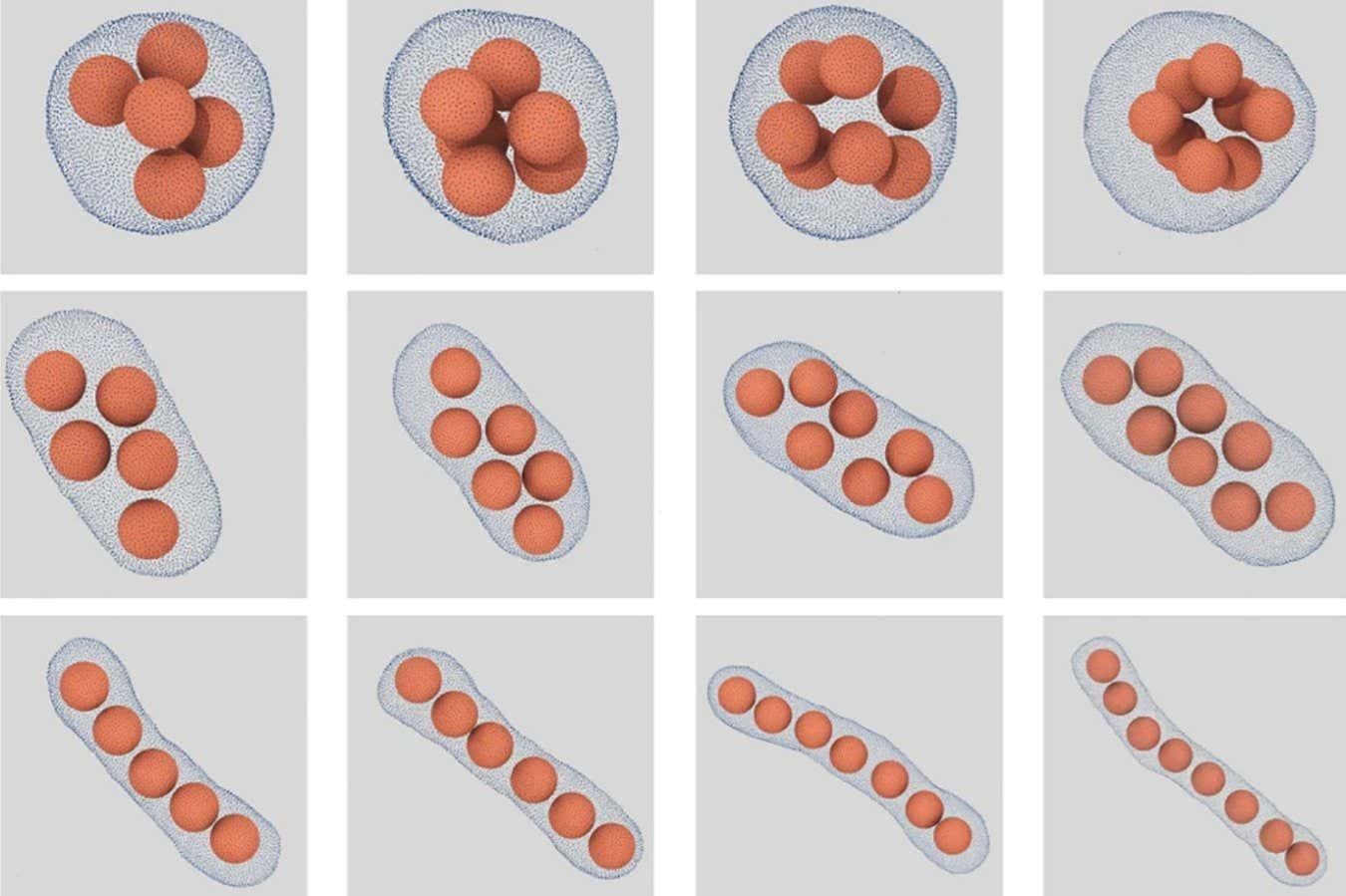
Mathematicians have long been fascinated by the most efficient way of packing spheres in a space, and now physicists have confirmed that the best place to put them is into a sausage shape, at least for small numbers of balls.
Simulations show microscopic plastic balls within a cell membrane
What is the most space-efficient way to pack tennis balls or oranges? Mathematicians have studied this “sphere-packing” problem for centuries, but surprisingly little attention has been paid to replicating the results in the real world. Now, physical experiments involving microscopic plastic balls have confirmed what mathematicians had long suspected – with a small number of balls, it is best to stick them in a sausage.
Kepler was the first person to tackle sphere packing, suggesting in 1611 that a pyramid would be the best way to pack cannonballs for long voyages, but this answer was only fully proven by mathematicians in 2014.
This proof only considers the best way of arranging an infinite number of spheres, however. For finite sphere packings, simply placing the balls in a line, or sausage, is more efficient until there are around 56 spheres. At this point, the balls experience what mathematicians call the “sausage catastrophe” and something closer to pyramid packing becomes more efficient.
But what about back in the real world? Sphere-packing theories assume that the balls are perfectly hard and don’t attract or repel each other, but this is rarely true in real life – think of the squish of a tennis ball or an orange.
One exception is microscopic polystyrene balls, which are very hard and basically inert. Hanumantha Rao Vutukuri at the University of Twente in the Netherlands and his team, who were unaware of mathematical sphere-packing theories, were experimenting with inserting these balls into empty cell membranes and were surprised to find them forming sausages.
“One of my students observed a linear packing, but it was quite puzzling,” says Vutukuri. “We thought that there was some fluke, so he repeated it a couple of times and every time he observed similar results,” says Vutukuri. “I was wondering, ‘why is this happening?’ It’s a bit counterintuitive.”
After reading up on sphere packing, Vutukuri and his team decided to investigate and carried out simulations for different numbers of polystyrene balls in a bag. They then compared their predictions with experiments using up to nine real polystyrene balls that had been squeezed into cell membranes immersed in a liquid solution. They could then shrink-wrap the balls by changing the concentration of the solution, causing the membranes to tighten, and see what formation the balls settled in using a microscope.
“For up to nine spheres, we showed, both experimentally and in simulations, that the sausage is the best packed,” says team member Marjolein Dijkstra at Utrecht University, the Netherlands. With more than nine balls, the membrane became deformed by the pressure of the balls. The team ran simulations for up to 150 balls and reproduced the sausage catastrophe, where it suddenly becomes more efficient to pack things in polyhedrons, with between 56 and 70 balls.
The sausage formation for a small number of balls is unintuitive, says Erich Müller at Imperial College London, but makes sense because of the large surface area of the membrane with respect to the balls at low numbers. “When dimensions become really, really small, then the wall effects become very important,” he says.
The findings could have applications in drug delivery, such as how to most efficiently fit hard antibiotic molecules, like gold, inside cell-like membranes, but the work doesn’t obviously translate at this point, says Müller.
For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to Alex Wilkins*