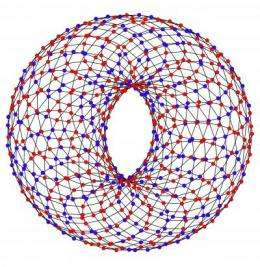
This is a simulation of a network of people playing Prisoner’s Dilemma. Red are cooperators; blue are defectors.
For the past twenty years, there has been a great controversy regarding whether the structure of interactions among individuals (that is, if the existence of a certain contact network or social network) helps to foment cooperation among them in situations in which not cooperating brings benefits without generating the costs of helping. Many theoretical studies have analysed this subject, but the conclusions have been contradictory since the way in which people make decisions is almost always based on a hypothesis of the models with very little basis to justify it.
The study carried out by these university researchers adopts a pioneering perspective on the theoretical study of the emergence of cooperation: rather than postulating that people make decisions according to one procedure or another, it incorporates the results obtained in experiments designed precisely to analyse how people decide whether to cooperate or not. The authors of the study are professors from the Interdisciplinary Complex Systems Group (Grupo Interdisciplinar de Sistemas Complejos – GISC) of the Mathematics Department of Carlos III University of Madrid, José Cuesta and Ángel Sánchez, together with Carlos Gracia and Yamir Moreno, from the Complex Systems and Networks Group (Grupo de Redes y Sistemas Complejos – COSNET Lab) of the Institute for Biocomputation and Physics of Complex Systems (Instituto de Biocomputación y Física de Sistemas Complejos – BIFI) of the University of Zaragoza. Their study was recently published in Scientific Reports, Nature’s new open access magazine.
This work is based on the results of an experiment carried out by the researchers and on information from other previous studies, as well as on the results (as yet unpublished) obtained from their own new experiments. The observations from these studies coincide in indicating that people do not consider what those they interact with gain; rather they think about whether or not they cooperate. In addition, their decisions usually depend on their own mood. That is, the authors noticed that the probability of cooperation occurring was considerably higher if there had been cooperation in the previous interaction. They also observed a certain heterogeneity in behaviour, finding a certain percentage of individuals who cooperated very little, regardless of what those around them did, and other individuals who almost always cooperated, again, no matter what others did.
These researchers have mathematically examined what occurs when groups of people who behave as the experiments say have to decide whether or not to cooperate, and how the existence of cooperation, globally or in the group, depends on the structure of the interactions. Specifically, the study analyses what happens if each person interacts with all of the others, if the people are placed in a square reticule and they interact with their four closest neighbours, or if they are arranged in a network that is more similar to a social network, in which the number of neighbours is highly variable and is dependent on each person. In the first case (each individual interacts with all of the others), the problem can be solved mathematically, so the level of resulting cooperation can be predicted. What the researchers observed is that this depends on the makeup of the population; that is, what proportion of the individuals use the previously described strategy, and what proportion almost always cooperates or almost never does, regardless of what the others do. Afterwards, this prediction can be compared with the results of numeric simulations obtains for the populations placed in each of the two networks, and it can be shown that the result is exactly the same, unlike what had been concluded in previous studies.
The consequences of this prediction are very important, according to the authors of the study, because if they are true, it would rule out the existence of one of the five mechanisms that have been proposed to explain the emergence of cooperation, the so-called “network reciprocity” mechanism. In order to prove the prediction, it will be necessary to carry out a large-scale experiment, something that this group of researchers in currently very involved in. These experiments are very difficult to carry out, given that studying heterogeneous networks in such a way as to obtain significant results, the team must work with hundred of volunteers simultaneously. If, as the team hopes, the experiments confirm what this study predicts, we would be witnessing a paradigm shift in the interpretation of decision-making in cooperative dilemmas: instead of considering what is to be gained, individuals would base their decisions on the cooperation they have received, and this would mean that the way that they interact (the underlying social network) would cease to be important.
For more such insights, log into our website https://international-maths-challenge.com
Credit of the article given to Carlos III University of Madrid