Month: November 1999

Economists from RUDN University have created a methodology based on mathematical modeling to manage production effectively with rapidly emerging innovations. The resultswere published in Sustainability.

Innovative products emerge so rapidly that enterprises have to change and adjust their management policies. Moreover, new management methods must ensure sustainable development. RUDN economists used mathematical modeling methods to develop a management methodology for enterprises that produce innovative products.

“An effective methodological tool for managing economic processes that ensure sustainable economic development of enterprises has not yet been developed. We set a goal to create such a tool based on mathematical modeling. Based on this tool, decision-makers could regulate processes, allocating additional resources and reducing risks,” said Zhanna Chupina, Ph.D., Associate Professor of the Department of Customs Affairs at RUDN University.

Economists have developed a tool that will allow, in modern conditions, to manage economic processes in such a way as to ensure sustainable development. To do this, the authors used mathematical modeling—they identified the main characteristics of the creation of innovative products and the activities of companies and described the dependence of profit on them. Economists included, for example, technical superiority over competitors, scientific and technological achievements based on the product, and price compliance with the capabilities of the buyer as the main values.

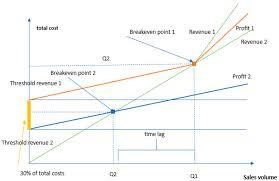
RUDN economists concluded that any innovation in a product is associated with the use or modernization of means of production. The authors determined the values of the technological level and the moments at which modernization should be carried out. It turned out that this needs to be done before the break-even point occurs, that is, the sales volume at which the proceeds from the sale of goods are equal to the costs of their production.

The general algorithm that economists have proposed is based on the fact that the properties of innovative products are involved in management. After management actions, it is necessary to evaluate the characteristics of the product and answer whether it is innovative. If so, then such an enterprise is considered capable of achieving global competitive superiority in the market. If not, then the characteristics need to be changed and return to the previous step.

“We have shown that for an organization to be in constant sustainable economic development, it is necessary to carry out updates to already produced innovative products even before the break-even point. We proposed a methodological toolkit to effectively manage the creation and production of innovative products and their renewal,” said Zhanna Chupina, Ph.D., associate professor of the Department of Customs Affairs at RUDN University.

For more such insights, log into our website https://international-maths-challenge.com

Credit of the article given to Russian Foundation for Basic Research

What better way is there to celebrate pi day than with a slice of mathematics? Here are 7 mathematical facts to enjoy.

There’s a mathematical trick to get out of any maze

It will soon be 14 March and that means pi day. We like to mark this annual celebration of the great mathematical constant at New Scientist by remembering some of our favourite recent stories from the world of mathematics. We have extracted a list of surprising facts from them to whet your appetite, but for the full pi day feast click through for the entire articles. These are normally only available to subscribers but to honour the world’s circumferences and diameters we have decided to make them free for a limited time.

The world’s best kitchen tile

There is a shape called “the hat” that can completely cover a surface without ever creating a repeating pattern. For decades, mathematicians had wondered whether a single tile existed that could do such a thing. Roger Penrose discovered pairs of tiles in the 1970s that could do the job but nobody could find a single tile that when laid out would have the same effect. That changed when the hat was discovered last year.

Why you’re so unique

You are one in a million. Or really, it should be 1 in a 10^{10^68.}  This number, dubbed the doppelgängion by mathematician Antonio Padilla, is so large it is hard to wrap your head around. It is 1 followed by 100 million trillion trillion trillion trillion trillion zeroes and relates to the chances of finding an exact you somewhere else in the universe. Imagining a number of that size is so difficult that the quantum physics required to calculate it seems almost easy in comparison. There are only a finite number of quantum states that can exist in a you-sized portion of space. You reach the doppelgängion by adding them all up. Padilla also wrote about four other mind-blowing numbers for New Scientist. Here they all are.

An amazing trick

There is a simple mathematical trick that will get you out of any maze: always turn right. No matter how complicated the maze, how many twists, turns and dead ends there are, the method always works. Now you know the trick, can you work out why it always leads to success?

And the next number is

There is a sequence of numbers so difficult to calculate that mathematicians have only just found the ninth in the series and it may be impossible to calculate the tenth. These numbers are called Dedekind numbers after mathematician Richard Dedekind and describe the number of possible ways a set of logical operations can be combined. When the set contains just a few elements, calculating the corresponding Dedekind number is relatively straightforward, but as the number of elements increases, the Dedekind number grows at “double exponential speed”. Number nine in the series is 42 digits long and took a month of calculation to find.

Can’t see the forest for the TREE(3)

There is a number so big that in can’t fit in the universe. TREE(3) comes from a simple mathematical game. The game involves generating a forest of trees using different combinations of seeds according to a few simple rules. If you have one type of seed, the largest forest allowed can have one tree. For two types of seed, the largest forest is three trees. But for three types of seed, well, the largest forest has TREE(3) trees, a number that is just too big for the universe.

The language of the universe

There is a system of eight-dimensional numbers called octonions that physicists are trying to use to mathematically describe the universe. The best way to understand octonions is first to consider taking the square root of -1. There is no such number that is the result of that calculation among the real numbers (which includes all the counting numbers, fractions, numbers like pi, etc.), so mathematicians add another called i. When combined with the real numbers, this gives a system called the complex numbers, which consist of a real part and an “imaginary part”, such as 3+7i. In other words, it is two-dimensional. Octonions arise by continuing to build up the system until you get to eight dimensions. It isn’t just mathematical fun and games though – there is reason to believe that octonions may be the number system we need to understand the laws of nature.

So many new solutions

Mathematicians went looking for solutions to the three-body problem and found 12,000 of them. The three-body problem is a classic astronomy problem of how three objects can form a stable orbit around each other. Such an arrangement is described by Isaac Newton’s laws of motion but actually finding permissible solutions is incredibly difficult. In 2007, mathematicians managed to find 1223 new solutions to the problem but this was greatly surpassed last year when a team found more than 12,000 more.

For more such insights, log into www.international-maths-challenge.com.

*Credit for article given to Timothy Revell*