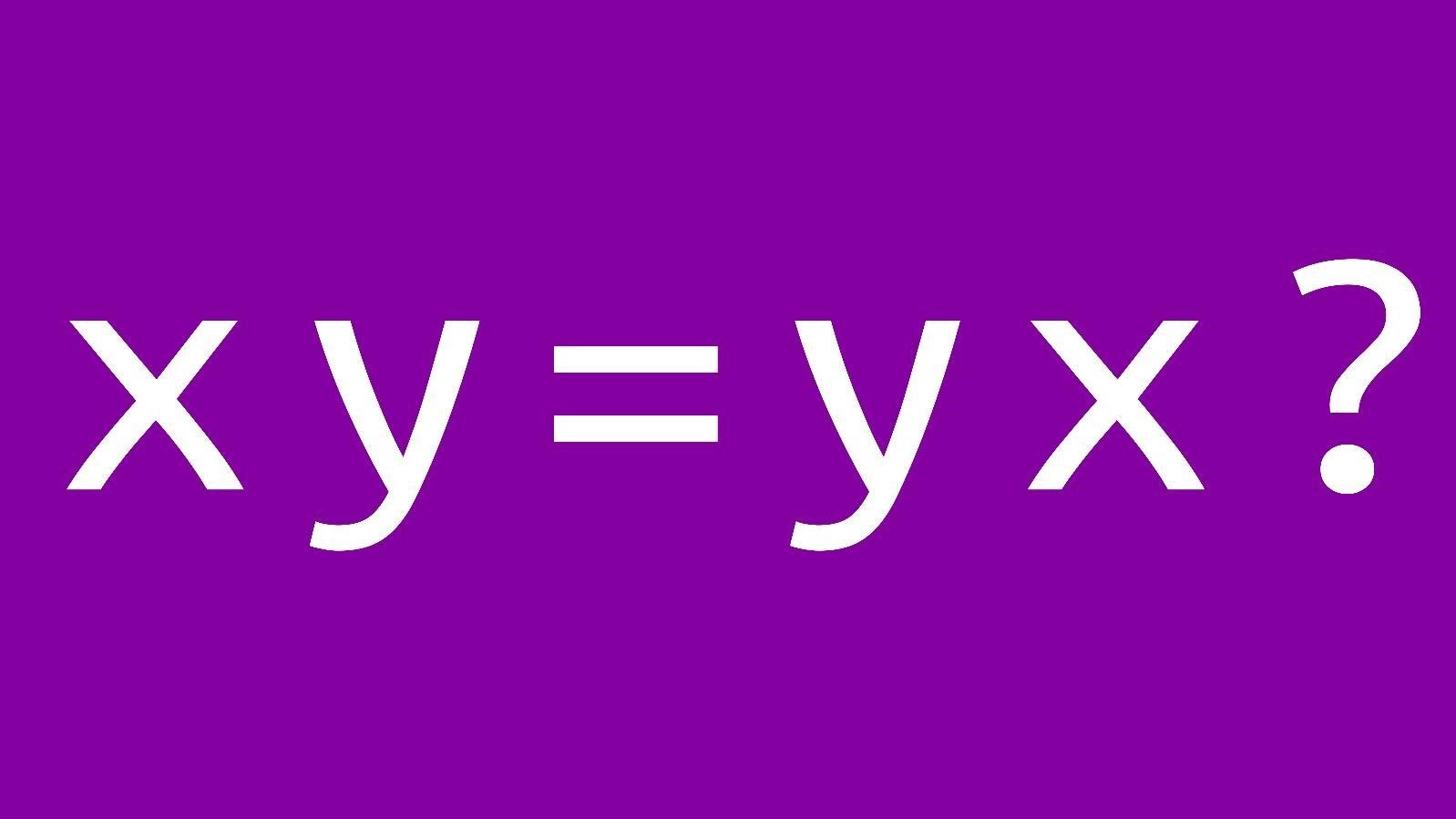After some exposure to group theory, you quickly learn that when trying to prove a group GG is abelian, checking if xy=yxxy=yx for arbitrary x,yx,y in GG is not always the most efficient – or helpful! – tactic. Here is a (not comprehensive) running tab of other ways you may be able to prove your group is abelian:
Show the commutator [x,y]=xyx−1y−1[x,y]=xyx−1y−1of two arbitary elements x,y∈Gx,y∈G must be the identity
- Show the group is isomorphic to a direct product of two abelian (sub)groups
- Check if the group has order p2p2 for any prime pp OR if the order is pqpq for primes p≤qp≤q with p∤q−1p∤q−1.
- Show the group is cyclic.
- Show |Z(G)|=|G|.|Z(G)|=|G|.
- Prove G/Z(G)G/Z(G) is cyclic. (e.g. does G/Z(G)G/Z(G) have prime order?)
- Show that GG has a trivial commutator subgroup, i.e. is [G,G]={e}[G,G]={e}.
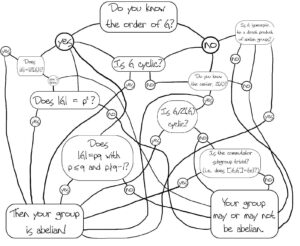
Here’s a thought map which is (probably) more fun than practical. Note, pp and qq denote primes below:
For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to Tai-Danae Bradley*