You thought the maze looked fun, but now you can’t find your way out. Luckily, mathematics is here to help you escape, says Katie Steckles.
Getting lost in a maze is no fun, and on that rare occasion when you find yourself stuck in one without a map or a bird’s-eye view, it can be difficult to choose which way to go. Mathematics gives us a few tools we can use – in particular, topology, which concerns shapes and how they connect.
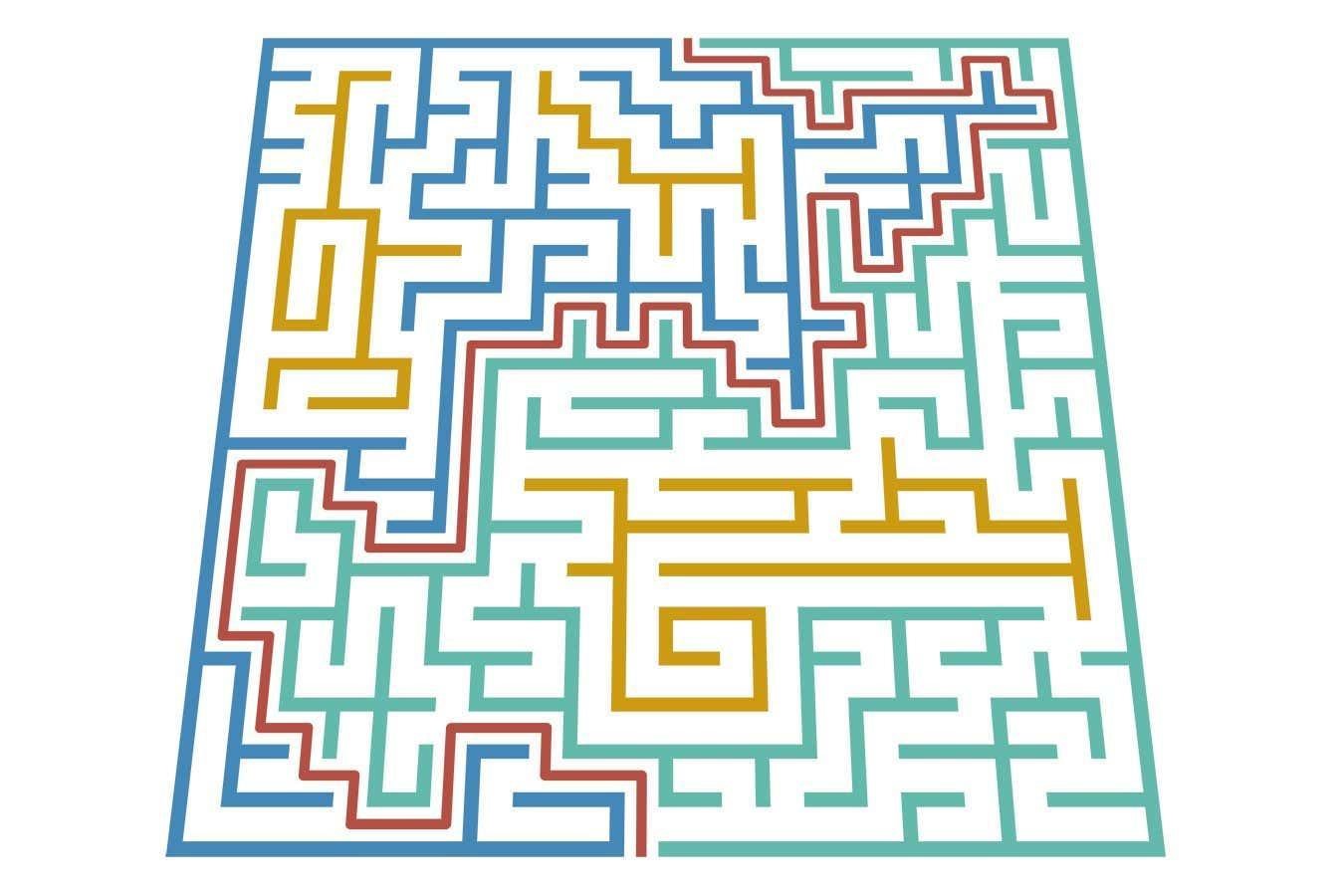
The most devious mazes are designed to be as confusing as possible, with dead ends and identical-looking junctions. But there is a stunningly simple rule that will always get you out of a maze, no matter how complicated: always turn right.
Any standard maze can be solved with this method (or its equivalent, the “always-turn-left” method). To do it, place one hand on the wall of the maze as you go in and keep it there. Each time you come to a junction, keep following the wall – if there is an opening on the side you are touching, take it; otherwise go straight. If you hit a dead end, turn around and carry on.
The reason this works is because the walls of any solvable maze will always have at least two distinct connected pieces: one to the left of the optimal solution path (shown in red), and one to the right. The section of wall next to the entrance is part of the same connected chunk of maze as the wall by the exit, and if you keep your hand on it, you will eventually walk along the whole length of the edge of this object – no matter how many twists and turns this involves – and reach the part at the exit.
While it is guaranteed to work, this certainly won’t be the most efficient path – you might find you traverse as much as half of the maze in the process, or even more depending on the layout. But at least it is easy to remember the rule.
Some mazes have more than two pieces. In these, disconnected sections of wall (shown in yellow) inside the maze create loops. In this case, if you start following the wall somewhere in the middle of the maze, there is a chance it could be part of an isolated section, which would leave you walking around a loop forever. But if you start from a wall that is connected to the outside, wall-following will still get you out.
It is reassuring to know that even if you are lost in a maze, you can always get out by following some variation on this rule: if you notice you have reached part of the maze you have been to before, you can detect loops, and switch to the opposite wall.
This is especially useful for mazes where the goal is to get to the centre: if the centre isn’t connected to the outside, wall-following won’t work, and you will need to switch walls to get onto the centre component. But as long as there are a finite number of pieces to the maze, and you keep trying different ones, you will eventually find a piece that is connected to your goal. You might, however, miss the bus home.
For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to Katie Steckles*