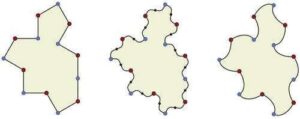
The 14-sided polygon Tile(1,1), on the left, is known as a weakly chiral aperiodic monotile — in other words, if tilings that mix unreflected and reflected tiles are forbidden, then it tiles only aperiodically. However, by modifying its edges, as shown in the centre and right, strictly chiral aperiodic monotiles called “spectres” are created that admit only non-periodic tilings. Credit: University of Waterloo
Recently, an international team of four, that includes Cheriton School of Computer Science professor Dr. Craig Kaplan, discovered a single shape that tiles the plane—an infinite, two-dimensional surface—in a pattern that can never be made to repeat.
The discovery mesmerized mathematicians, tiling enthusiasts and the public alike.
The shape, a 13-sided polygon they called “the hat,” is known to mathematicians as an aperiodic monotile or an “einstein,” the German words that mean “one stone.”
But the team’s most recent discovery has raised the bar once again. They found another shape, related to the first, that meets an even stricter definition. Dubbed the “specter,” the new shape tiles a plane in a pattern that never repeats without the use of mirror images of the shape. For this reason, it has also been called a “vampire einstein”—a shape that tiles aperiodically without requiring its reflection.
“Our first paper solved the einstein problem, but as the shape required reflection to tile aperiodically people raised a legitimate question: Is there a shape that can do what the hat does but without reflection,” Kaplan explains. “It was our good fortune that we found a shape that not only solves this subproblem, but also solved it so soon after the first paper.”
To mathematicians, the hat and its mirror image are a single shape, but in the physical world left-handed and right-handed shapes can behave differently. You can’t, for example, wear a right-handed glove on your left hand.
“If you tiled a large bathroom floor aperiodically with hat-shaped tiles that had been glazed on one side you would need hats and mirror images of hats,” Kaplan says.
But it was not this quibble that motivated the recent discovery.
The discovery of the vampire einstein began with the musings of David Smith, a retired print technician and self-described shape hobbyist from Yorkshire, England, whose curiosity months earlier led to the original einstein discovery.
“Dave emailed us a couple of days after our hat paper went online to say that he had been playing around with a related shape that seemed to be behaving strangely,” Kaplan says. “Yoshiaki Araki, a Japanese mathematician and well-known artist whose work is in the spirit of MC Escher, had posted pictures of Tile(1,1) that got Dave interested in looking at it further.”
Yoshiaki posted an intriguing question on Twitter: “An aperiodic turtle tessellation based on new aperiodic monotile Tile(1, 1.1). In the tiling, it is said that around 12.7% of tiles are reflected. The green one is an instance. One more reflected turtle is hidden in the tiling. Who is the reflected?'”
“Yoshi had turned Tile(1,1) into turtles and it’s a bit hard to see the other reflected turtle in that picture. But it got Dave curious. What if we tile with this shape but without reflections? As he did that, Dave found that he could build tilings progressively outward in a pattern that didn’t stop and didn’t repeat.”
But then this shape came with a different quibble. As Kaplan explains, if you use reflections of Tile(1,1) the pattern does repeat. In other words, it’s periodic. But if Tile(1,1) is modified by replacing its straight edges with curves, it becomes a vampire einstein—a single shape that without reflection tiles the infinite plane in a pattern that can never be made to repeat.
The obvious question for mathematicians and tiling enthusiasts is what’s next?
“We can pose many variations of the problem,” Kaplan says. “The most interesting, for me at least, is whether this can be done in 3D. It would be nice to have a shape that repeats non-periodically in three dimensions. Such constructions are much harder to visualize, but computationally it’s not that much more difficult to prove should we be so lucky as to find a three-dimensional shape—a polyform—that like the hat tiles only aperiodically.”
“Tiling theory as a branch of mathematics is beautiful, tangible, and has a lot of fascinating problems to be solved. There’s no shortage of follow-up work to be done.”
Hatfest, a celebration of the discovery of “the Hat,” will be taking place at the University of Oxford’s Mathematical Institute from July 20 to 21. The event’s first day will feature talks and workshops on tiling aimed at a lay audience, while the second will feature presentations aimed at a broad audience of physicists and mathematicians.
For more such insights, log into our website https://international-maths-challenge.com
Credit of the article given to Joe Petrik, University of Waterloo

