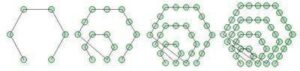
Polygonal numbers are a mainstay of recreational and school mathematics, providing a nice bridge between numbers and shapes. The diagrams above show some of the hexagonal numbers.
Some examples of two-dimensional polygonal numbers are:
the triangular numbers: 1, 3, 6, 10, 15, …
the square numbers: 1, 4, 9, 16, 25, …
the pentagonal numbers: 1, 5, 12, 22, 35,…
the hexagonal numbers: 1, 6, 15, 28, 45, …
Comparing the listing for the hexagonal numbers with the diagrams above, you can see how the sequences are built diagrammatically. In general, beginning with a single dot, k-sided polygons are built by adding layers (called gnomons) consisting of k-2 segments, with each segment of the gnomon having one more dot than the segments of the previous layer. In this way, the nth gnomon consists of segments each n dots long, but with k-3 dots shared by adjoining segments (the corners).
The description above can lead you to a recursive formula for k-polygonals, writing p_k,n for the nth k-polygonal number:
![]()
Unwinding the recursion gives you a summation formula for k-polygonals:
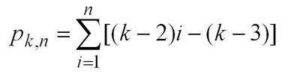
Knowing a little about sums gives you the direct formula for k-polygonals:
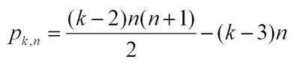
Coming a little out of left-field is this combinatorial formula for k-polygonals:
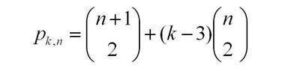
This last formula expresses two ideas: that the triangular numbers correspond to the r=0 column of Pascal’s triangle, and that every polygonal number can be “triangulated”:
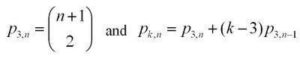
The combinatorial formula for p_kn can be generalized to higher-dimensional polygonal numbers (pyrimidal numbers, etc.).
The recreation here lies in showing that the various formulas for p_k,n are really the same, and then exploring the relationships between the different k-polygonals. A great resource is J.H. Conway and R.K. Guy’s The Book of Numbers.a
For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to dan.mackinnon*

