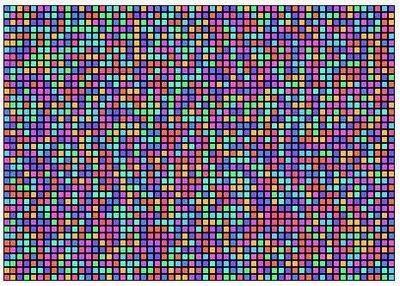
John Sims has created a number of pi-related art works. One, the Pi Color Map, can be recreated effectively using TinkerPlots. The image above is one such Pi Color Map, using 2281 digits of pi.
Here are some instructions for creating a Pi Color Map in Tinkerplots.
1. Obtain a listing of the digits of pi – up to a reasonable number. You can get the digits from several sites, including the pi day site.
2. Paste your listing to a text document, and get them arranged into a single column. One strategy for doing this is and use the find/replace feature of a word-processor to replace each number with the number itself plus a line-break(e.g. in Word, replace 2 with 2^l, etc.).
3. If you’ve included the decimal point, remove it. For the first line of your document, provide a heading like pi_expansion. This will be your TinkerPlots attribute.
3. Import the text file into TinkerPlots using the File>Import menu.
4. Create a new attribute called digit whose formula is digit=concat(“”,pi_expansion). This creates a categorical data type that TinkerPlots won’t treat numerically. This is what you will use as your color key. Using the pi_expansion attribute gives a spectrum of color, rather than distinct colors for each number.
5. Create a new attribute called place, whose formula is place=caseIndex. This is what you will order your plot by.
6. Create a new plot, lock the color key on the digit attribute. Select the place attribute and press the Order By button.
7. Change your icon type to small squares, and stack the cases.
You can play with different options to get different effects for your color map.
One nice thing about doing this in TinkerPlots is that you can investigate the data further. The color map plot highlights the apparent randomness of the pi expansion, but you can also create other attributes and plots to investigate things like the running average of the digits, occurrences of consecutive digits, and the overall distribution of the digits (it should be uniform).

For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to dan.mackinnon*