Example 5
A sequence of functions {fn:R→R}{fn:R→R} which converges to 0 pointwise but does not converge to 0 in L1L1.
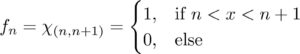
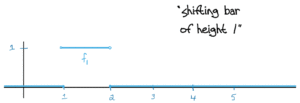
This works because: The sequence tends to 0 pointwise since for a fixed x∈Rx∈R, you can always find N∈NN∈N so that fn(x)=0fn(x)=0 for all nn bigger than NN. (Just choose N>xN>x!)
The details: Let x∈Rx∈R and fix ϵ>0ϵ>0 and choose N∈NN∈N so that N>xN>x. Then whenever n>Nn>N, we have |fn(x)−0|=0<ϵ|fn(x)−0|=0<ϵ.
Of course, fn↛0fn↛0 in L1L1 since∫R|fn|=∫(n,n+1)fn=1⋅λ((n,n+1))=1.
For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to Tai-Danae Bradley*