This post is the fourth example in an ongoing list of various sequences of functions which converge to different things in different ways.
Also in this series:
Example 1: converges almost everywhere but not in L1L1
Example 2: converges uniformly but not in L1L1
Example 3: converges in L1L1 but not uniformly
Example 5: converges pointwise but not in L1L1
Example 6: converges in L1L1 but does not converge anywhere
Example 4
A sequence of (Lebesgue) integrable functions fn:R→[0,∞)fn:R→[0,∞) so that {fn}{fn} converges to f:R→[0,∞)f:R→[0,∞) uniformly, yet ff is not (Lebesgue) integrable.
Our first observation is that “ff is not (Lebesgue) integrable” can mean one of two things: either ff is not measurable or ∫f=∞∫f=∞. The latter tends to be easier to think about, so we’ll do just that. Now what function do you know of such that when you “sum it up” you get infinity? How about something that behaves like the divergent geometric series? Say, its continuous cousin f(x)=1xf(x)=1x? That should work since we know∫R1x=∫∞11x=∞.∫R1x=∫1∞1x=∞.Now we need to construct a sequence of integrable functions {fn}{fn} whose uniform limit is 1x1x. Let’s think simple: think of drawring the graph of f(x)f(x) one “integral piece” at a time. In other words, define:
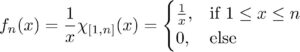
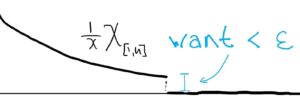
This works because: It makes sense to define the fnfn as f(x)=1xf(x)=1x “chunk by chunk” since this way the convergence is guaranteed to be uniform. Why? Because how far out we need to go in the sequence so that the difference f(x)−fn(x)f(x)−fn(x) is less than ϵϵ only depends on how small (or large) ϵϵ is. The location of xx doesn’t matter!
Also notice we have to define fn(x)=0fn(x)=0 for all x<1x<1 to avoid the trouble spot ln(0)ln(0) in the integral ∫fn∫fn. This also ensures that the area under each fnfn is finite, guaranteeing integrability.
The details: Each fnfn is integrable since for a fixed nn,∫Rfn=∫n11x=ln(n).∫Rfn=∫1n1x=ln(n).To see fn→ffn→f uniformly, let ϵ>0ϵ>0 and choose NN so that N>1/ϵN>1/ϵ. Let x∈Rx∈R. If x≤1x≤1, any nn will do, so suppose x>1x>1 and let n>Nn>N. If 1<x≤n1<x≤n, then we have |fn(x)−f(x)|=0<ϵ|fn(x)−f(x)|=0<ϵ. And if x>nx>n, then∣∣1xχ[1,∞)(x)−1xχ[1,n](x)∣∣=∣∣1x−0∣∣=1x<1n<1N<ϵ.|1xχ[1,∞)(x)−1xχ[1,n](x)|=|1x−0|=1x<1n<1N<ϵ.
For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to Tai-Danae Bradley*

