This post is the second example in an ongoing list of various sequences of functions which converge to different things in different ways.
Example 2
A sequence of functions {fn:R→R}{fn:R→R} which converges to 0 uniformly but does not converge to 0 in L1L1.
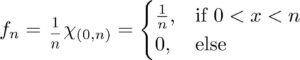
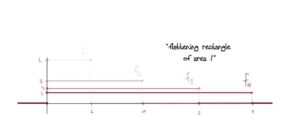
This works because: The sequence tends to 0 as n→∞n→∞ since the height of each function tends to 0 and the the region where fnfn is taking on this decreasing height is tending towards all of R+R+ ((0,n)(0,n) as n→∞n→∞) (and it’s already 0 on R−∪{0}R−∪{0}). The convergence is uniform because the number of times we have to keep “squishing” the rectangles until their height is less than ϵϵ does not depend on xx.
The details: Let ϵ>0ϵ>0 and choose N∈NN∈N so that N>1ϵN>1ϵ and let n>Nn>N. Fix x∈Rx∈R.
Case 1 (x≤0x≤0 or x≥nx≥n) Then fn(x)=0fn(x)=0 and so |fn(x)−0|=0<ϵ|fn(x)−0|=0<ϵ.
- Case 2 (0<x<n0<x<n ) Then fn(x)=1nfn(x)=1n and so |fn(x)−0|=1n<1N<ϵ|fn(x)−0|=1n<1N<ϵ
Finally, fn↛0fn↛0 in L1L1 since∫R|fn|=∫(0,n)1n=1nλ((0,n))=1.∫R|fn|=∫(0,n)1n=1nλ((0,n))=1.
Remark: Here’s a question you could ask: wouldn’t fn=nχ(0,1n)fn=nχ(0,1n) work here too? Both are tending to 0 everywhere and both involve rectangles of area 1. The answer is “kinda.” The problem is that the convergence of nχ(0,1n)nχ(0,1n) is pointwise. BUT Egoroff’s Theorem gives us a way to actually “make” it uniform!.
On the notation above: For a measurable set X⊂RX⊂R, denote the set of all Lebesgue integrable functions f:X→Rf:X→R by L1(X)L1(X). Then a sequence of functions {fn}{fn} is said to converge in L1L1 to a function ff if limn→∞∫|fn−f|=0limn→∞∫|fn−f|=0.
For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to Tai-Danae Bradley*

