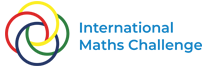Given a sequence of real-valued functions {fn}{fn}, the phrase, “fnfn converges to a function ff” can mean a few things:
- fnfn converges uniformly
- fnfn converges pointwise
- fnfn converges almost everywhere (a.e.)
- fnfn converges in L1L1 (set of Lebesgue integrable functions)
- and so on…
Other factors come into play if the fnfn are required to be continuous, defined on a compact set, integrable, etc.. So since I do not have the memory of an elephant (whatever that phrase means…), I’ve decided to keep a list of different sequences that converge (or don’t converge) to different functions in different ways. With each example I’ll also include a little (and hopefully) intuitive explanation for why. Having these sequences close at hand is especially useful when analysing the behavior of certain functions or constructing counterexamples.
The first sequence we’ll look at is one which converges almost everywhere, but does not converge in L1L1 (the set of Lebesgue integrable functions).
Example 1
A sequence of functions {fn:R→R}{fn:R→R} which converges to 0 almost everywhere but does not converge to 0 in L1L1. 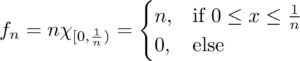
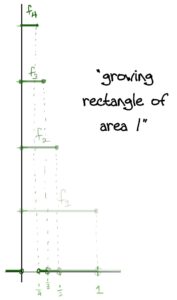
This works because: Recall that to say fn→0fn→0 almost everywhere means fn→0fn→0 pointwise on RR except for a set of measure 0. Here, the set of measure zero is the singleton set {0}{0} (at x=0x=0, fn(x)=nfn(x)=n and we can’t make this less than ϵϵ for any ϵ>0ϵ>0). So fnfn converges to 0 pointwise on (0,1](0,1]. This holds because if x<0x<0 or x>1x>1 then fn(x)=0fn(x)=0 for all nn. Otherwise, if x∈(0,1]x∈(0,1], we can choose nn appropriately:
The details: Let ϵ>0ϵ>0 and x∈(0,1]x∈(0,1] and choose N∈NN∈N so that N>1xN>1x. Then whenever n>Nn>N, we have n>1xn>1x which implies x>1nx>1n and so fn(x)=0fn(x)=0. Hence |fnx−0|=0<ϵ|fnx−0|=0<ϵ.
Further*, fn↛0fn↛0 in L1L1 since∫R|fn|=∫[0,1n]n=nλ([0,1n])=1.∫R|fn|=∫[0,1n]n=nλ([0,1n])=1.
Remark: Notice that Egoroff’s theorem applies here! We just proved that fn→0fn→0 pointwise a.e. on RR, but Egoroff says that we can actually get uniform convergence a.e. on a bounded subset of RR, say (0,1](0,1].
In particular for each ϵ>0ϵ>0 we are guaranteed the existence of a subset E⊂(0,1]E⊂(0,1] such that fn→0fn→0 uniformly and λ((0,1]∖E)<ϵλ((0,1]∖E)<ϵ. In fact, it should be clear that that subset must be something like (ϵ2,1](ϵ2,1] (the “zero region” in the graph above). Then no matter where xx is in (0,1](0,1], we can always find nn large enough – namely all nn which satisfy 1n<ϵ21n<ϵ2 – so that fn(x)=0fn(x)=0, i.e. fn→ffn→f uniformly. And indeed, λ((0,1]∖(ϵ2,1]=ϵ/2<ϵλ((0,1]∖(ϵ2,1]=ϵ/2<ϵ as claimed.
On the notation above: For a measurable set X⊂RX⊂R, denote the set of all Lebesgue integrable functions f:X→Rf:X→R by L1(X)L1(X). Then a sequence of functions {fn}{fn} is said to converge in L1L1 to a function ff if limn→∞∫|fn−f|=0limn→∞∫|fn−f|=0.
For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to Tai-Danae Bradley*