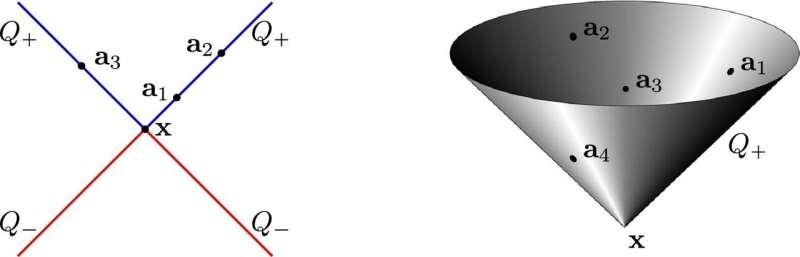
All ai lie on the same sheet of a cone with vertex x. The right-hand picture is not true to scale relative to the given numerical example. Credit: Advances in Applied Mathematics (2024). DOI: 10.1016/j.aam.2024.102741
The summer holidays are ending, which for many concludes with a long drive home and reliance on GPS devices to get safely home. But every now and then, GPS devices can suggest strange directions or get briefly confused about your location. But until now, no one knew for sure when the satellites were in a good enough position for the GPS system to give reliable direction.
TU/e’s Mireille Boutin and her co-worker Gregor Kemper at the Technical University of Munich have turned to mathematics to help determine when your GPS system has enough information to determine your location accurately. The research is published in the journal Advances in Applied Mathematics.
“In 200 meters, turn right.” This is a typical instruction that many have heard from their global positioning system (GPS).
Without a doubt, advancements in GPS technologies and mobile navigation apps have helped GPS play a major role in modern car journeys.
But, strictly adhering to instructions from GPS devices can lead to undesirable situations. Less serious might be turning left instead of right, while more serious could be driving your car into a harbor—just as two tourists did in Hawaii in 2023. The latter incident is very much an exception to the rule, and one might wonder: “How often does this happen and why?”
GPS and your visibility
“The core of the GPS system was developed in the mid-1960s. At the time, the theory behind it did not provide any guarantee that the location given would be correct,” says Boutin, professor at the Department of Mathematics and Computer Science.
It won’t come as a surprise then to learn that calculating an object’s position on Earth relies on some nifty mathematics. And they haven’t changed much since the early days. These are at the core of the GPS system we all use. And it deserved an update.
So, along with her colleague Gregor Kemper at the Technical University of Munich, Boutin turned to mathematics to expand on the theory behind the GPS system, and their finding has recently been published in the journal Advances in Applied Mathematics.
How does GPS work?
Before revealing Boutin and Kemper’s big finding, just how does GPS work?
Global positioning is all about determining the position of a device on Earth using signals sent by satellites. A signal sent by a satellite carries two key pieces of information—the position of the satellite in space and the time at which the position was sent by the satellite. By the way, the time is recorded by a very precise clock on board the satellite, which is usually an atomic clock.
Thanks to the atomic clock, satellites send very accurate times, but the big issue lies with the accuracy of the clock in the user’s device—whether it’s a GPS navigation device, a smartphone, or a running watch.
“In effect, GPS combines precise and imprecise information to figure out where a device is located,” says Boutin. “GPS might be widely used, but we could not find any theoretical basis to guarantee that the position obtained from the satellite signals is unique and accurate.”
Google says ‘four’
If you do a quick Google search for the minimum number of satellites needed for navigation with GPS, multiple sources report that you need at least four satellites.
But the question is not just how many satellites you can see, but also what arrangements can they form? For some arrangements, determining the user position is impossible. But what arrangements exactly? That’s what the researchers wanted to find out.
“We found conjectures in scientific papers that seem to be widely accepted, but we could not find any rigorous argument to support them anywhere. Therefore, we thought that, as mathematicians, we might be able to fill that knowledge gap,” Boutin says.
To solve the problem, Boutin and Kemper simplified the GPS problem to what works best in practice: equations that are linear in terms of the unknown variables.
“A set of linear equations is the simplest form of equations we could hope for. To be honest, we were surprised that this simple set of linear equations for the GPS problem wasn’t already known,” Boutin adds.
The problem of uniqueness
With their linear equations ready, Boutin and Kemper then looked closely at the solutions to the equations, paying special attention as to whether the equations gave a unique solution.
“A unique solution implies that the only solution to the equations is the actual position of the user,” notes Boutin.
If there is more than one solution to the equations, then only one is correct—that is, the true user position—but the GPS system would not know which one to pick and might return the wrong one.
The researchers found that nonunique solutions can emerge when the satellites lie in a special structure known as a “hyperboloid of revolution of two sheets.”
“It doesn’t matter how many satellites send a signal—if they all lie on one of these hyperboloids then it’s possible that the equations can have two solutions, so the one chosen by the GPS could be wrong,” says Boutin.
But what about the claim that you need at least four satellites to determine your position? “Having four satellites can work, but the solution is not always unique,” points out Boutin.
Why mathematics matters
For Boutin, this work demonstrates the power and application of mathematics.
“I personally love the fact that mathematics is a very powerful tool with lots of practical applications,” says Boutin. “I think people who are not mathematicians may not see the connections so easily, and so it is always nice to find clear and compelling examples of everyday problems where mathematics can make a difference.”
Central to Boutin and Kemper’s research is the field of algebraic geometry in which abstract algebraic methods are used to solve geometrical, real-world problems.
“Algebraic geometry is an area of mathematics that is considered very abstract. I find it nice to be reminded that any piece of mathematics, however abstract it might be, may turn out to have practical applications at some point,” says Boutin.
For more such insights, log into our website https://international-maths-challenge.com
Credit of the article to be given Eindhoven University of Technology