
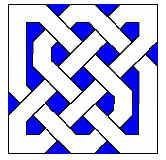
Knot patterns (which might not actually represent knots, but just braids or plaits), like the one shown here, are common in Celtic design.
One way to create knot patterns is to use a set of tiles that are put together following a few basic rules. This is not, as far as I know, a standard way to create these patterns – the book by Aidan Meehan, provides a technique for drawing the patterns by hand, rather than laying them out as tiles.
A wide range of knot patterns, including the one shown above, can be created using the set of six tiles shown below. These were constructed using Geometer’s Sketchpad.

The rules for putting these together are reasonably clear, but can be formalized. You can even come up with a notation for the tiles and formal rules for assembling them into knot patterns.
When laying down the tiles, you have the option of rotating them – some of the tiles don’t alter with rotation, some of them can be placed in two ways, some in four.
A nice property of this set is that you can’t paint yourself into a corner when using it – you can always find a tile that will compose with the pattern that you have started. This property means that this set of tiles is closed, in a certain sense.
A wider range of patterns can be created if you add tiles like the ones below to your set.

Unfortunately, when you include these tiles, your set is no longer closed. An open question (at least as far as I know) is – how many more tiles would you need to add in order to create a closed set of tiles that includes these? Also, what would these tiles look like? Do they lead to “reasonable” looking knots?
The knot pattern below (better described as a woven set of three links) was made using tiles including the ones from the “extended” set above.
For more such insights, log into www.international-maths-challenge.com.
*Credit for article given to dan.mackinnon*
